Optymalna wielkość zamówienia
Optymalna wielkość zamówienia (dostawy) wykorzystywana jest w zarządzaniu zapasami przedsiębiorstwa. Główną funkcją zapasów w przedsiębiorstwie jest zapewnienie ciągłości działalności gospodarczej.
Niedostateczne zapasy materiałów i produktów mogą przerwać ciągłość procesu produkcji i sprzedaży, a tym samym spowodować straty przedsiębiorstwa. Natomiast zbyt duża ilość zapasów łączy się ze zbędnymi kosztami magazynowania.
Zapasy zmniejszają wrażliwość firmy na zakłócenia w procesie dostaw oraz zwiększają elastyczność przedsiębiorstwa względem klientów poprzez realizację zamówień w odpowiedniej ilości i w odpowiednim czasie. W warunkach wysokiej inflacji pozwalają na uzyskanie korzyści związanych ze wzrostem cen zaopatrzeniowych. Zarządzanie zapasami uwzględnia korzyści i koszty posiadania zapasów.
Gdy wzrastają zapasy materiałowe i towary następuje wzrost jednorazowych zamówień i częstotliwość dostaw spada. Powoduje to spadek kosztów związanych z pozyskiwaniem materiałów i surowców. Zamawiając większą partię materiałów nabywca może uzyskać lepsze warunki płatności (np. dłuższe terminy), opusty cenowe, może wybrać tańszy środek transportu. Spadają także koszty manipulacyjne związane z samym procesem zamawiania, takie jak koszty składania zamówień, koszty prowadzenia ksiąg rachunkowych, koszty przyjęcia materiałów i towarów do magazynu, koszty ewidencjonowania dostaw itp. Równocześnie maleją również prawdopodobne straty z tytułu ewentualnych przestojów produkcyjnych lub utraty klientów spowodowane brakiem towarów. W miarę wzrostu wielkości zamówienia koszty jego realizacji przypadające na jednostkę zapasu są niższe.
Całkowite koszty zapasów materiałów składają się z kosztów posiadania zapasów i kosztów realizacji zamówienia. W obydwóch grupach kosztów występują pozycje zależne i niezależne od wielkości jednorazowego zamówienia. Na przykład koszty utrzymania powierzchni magazynowej nie są zależne od wielkości dostaw. Z kolei koszty kapitałowe, koszty ubezpieczenia wzrastają w miarę wzrostu ich poziomu. W grupie kosztów realizacji zamówienia stały charakter (niezależny od wielkości jednorazowego zamówienia) mają koszty manipulacyjne.
Optymalna wielkość zamówienia to taka wielkość zamówienia, przy której przebieg procesu produkcji jest niezakłócony oraz następuje minimalizacja kosztów związanych z magazynowaniem i przechowywaniem.
Wielkość ta kształtowana jest na takim poziomie, aby łączne koszty utrzymywania zapasów (koszty posiadania zapasów i koszty realizacji zamówienia) były jak najniższe.
Optymalna wielkość zamówienia determinuje optymalną częstotliwość dostaw.
Przy określaniu optymalnej wielkości pojedynczego zamówienia należy opierać się na analizie dwóch czynników:
- charakteru i wielkości zapotrzebowania na poszczególne materiały i surowce wykorzystywane w procesie produkcji (wyznaczanych przez poziom produkcji i poziom zużycia surowców i materiałów na wyprodukowanie jednostki wyrobu, przy znajomości skali produkcji mogą być określane za pomocą dokumentacji konstrukcyjno-technologicznej)
- kosztów zakupu (obejmujące koszty związane z dokonaniem zamówienia, koszty ubezpieczenia transportu, koszty transportu, koszty przyjęcia do magazynu itd.) oraz magazynowania tych materiałów i surowców (np. koszty dzierżawy i najmu powierzchni magazynowej, straty wynikające z zepsucia lub ubytków przechowywanych materiałów i surowców).
W celu korzystania ze strategii optymalnej wielkości zamówienia należy dokonać pewnych założeń:
- znany i stały koszt utrzymania zapasu
- znany i stały koszt zamawiania
- znane rozmiary popytu
- znany i stały koszt jednostkowy zamawianego surowca
- odnowienie zapasu ma charakter całkowity, tj. zamawiana wielkość dostarczana jest w całości (Terence Lucey, 2002, s. 239)
Metoda ta jest szczególnie przydatna przy zarządzaniu zapasami przedsiębiorstw dla których zapotrzebowanie na zapasy cechuje się powtarzalnością (np. zaopatrzenie szpitali). Wyznaczanie optymalnej wielkości zamówienia może być zastosowane do każdego składnika zapasów (Andrew J. Du Brin 2008, s. 206)
TL;DR
Optymalna wielkość zamówienia jest kluczowa dla zarządzania zapasami w przedsiębiorstwie. Niedostateczne zapasy mogą przerwać proces produkcji, a zbyt duże zapasy wiążą się z kosztami. Optymalna wielkość zamówienia minimalizuje koszty związane z magazynowaniem i przechowywaniem. Może być obliczana graficznie lub matematycznie. Optymalna wielkość zamówienia nie uwzględnia rabatów cenowych, dlatego należy również rozważyć korzyści związane z niższą ceną jednostkową przy większych zamówieniach.
Wyznaczanie optymalnej wielkości zamówienia metodą graficzną
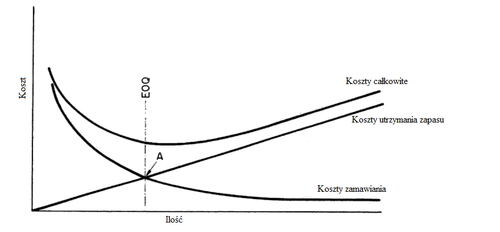
Wielkość odnawianego zapasu jest określana poprzez zbalansowanie kosztu utrzymania i zamawiania zapasu. Zrównoważenie tych dwóch wielkości skutkuje wyznaczeniem optymalnej wielkości zamówienia, a jednocześnie ponoszeniem minimalnego kosztu przez przedsiębiorstwo. Zamawiający wie, że w przypadku zamówienia mniejszej ilości koszt utrzymania zapasu maleje, ale rosną koszty zamawiania i na odwrót.
Na Rysunku 1, punkt przecięcia krzywych reprezentujących koszty utrzymania i zamawiania zapasu wyznacza taką wielkość zamówienia przy której koszty całkowite związane z zamawianiem i utrzymaniem zapasu są minimalne.
Wyznaczanie optymalnej wielkości zamówienia metodą matematyczną
Bardziej powszechną metodą wyznaczania optymalnej wielkości zamówienia jest obliczanie jej ze wzoru. Pozwala to na uzyskanie dokładnej wielkości zamówienia przy której całkowite koszty związane z zapasem są minimalne (Terence Lucey, 2002, s 241). Do zastosowania wzoru matematycznego konieczne jest obliczenie poszczególnych wielkości, są to:
- S - zużycie materiałowe określonego rodzaju lub grupy asortymentu (związane z przyjętą normą technologiczną) wyrażone w jednostkach naturalnych w danym okresie dla danej wielkości produkcji,
- O - koszt jednostkowy zamówionych materiałów zaopatrzeniowych (np. cena)
- C- koszty stałe związane z magazynowaniem zamówionych materiałów w danym okresie.
Optymalną wielkość zamówienia (EOQ) wyraża wzór:
- EOQ=
Optymalna wielkość zamówienia a korzystanie z rabatów
Optymalna wielkość zamówienia nie bierze pod uwagę możliwości korzystania z rabatów cenowych związanych z zamawianiem konkretnej ilości zapasu. W rzeczywistości biznesowej, dostawcy często oferują niższą cenę jednostkową produktu w przypadku składania zamówień na większe ilości. W takim wypadku osoba składająca zamówienie musi wziąć pod uwagę potencjalne korzyści wynikające z niższej ceny jednostkowej oraz mniejszej ilości zamówień w ciągu roku. Zadaniem zamawiającego jest wtedy określenie ilości zamówienia gwarantującej minimalny koszt całkowity.
Koszt całkowity jest sumą następujących elementów:
- Koszt utrzymania
- Koszt zamawiania
- Koszt produktów
Procedurę wyznaczania rozwiązania optymalnego przedstawiono poniżej:
- Obliczenie optymalnej wielkości zamówienia zgodnie ze wzorem, przy jednoczesnym pominięciu obniżonej ceny jednostkowej, a następnie obliczenie kosztów całkowitych (EOQ)
- Obliczenie optymalnej wielkości zamówienia zgodnie ze wzorem, przy jednoczesnym uwzględnieniu obniżonej ceny jednostkowej (EOQd)
- Jeżeli EOQd > Qd, gdzie Qd oznacza wielkość zamówienia upoważniającą do korzystania z rabatu, wtedy EOQd jest nową optymalną wielkością zamówienia
- Jeżeli EOQd < Qd, gdzie Qd oznacza wielkość zamówienia upoważniającą do korzystania z rabatu, wtedy należy obliczyć koszt całkowity osiągany przy składaniu zamówienia na ilość Qd
- Jeżeli koszt całkowity osiągany przy ilości Qd jest niższy niż w przypadku ilości równej EOQ, Qd jest nową optymalną wielkością zamówienia (Joel G. Siegel, 2006, s. 795)
| Optymalna wielkość zamówienia — artykuły polecane |
| Zapas bezpieczeństwa — Gospodarka magazynowa — Gospodarowanie zapasami — Zarządzanie zapasami — Koszt zmienny — Ekonomiczna wielkość partii — Zdolność produkcyjna — Koszt stały — Zarządzanie cenami |
Bibliografia
- Czekaj J., Dresler Z. (1995), Podstawy zarządzania finansami firm, Wydawnictwo Naukowe PWN, Warszawa
- DuBrin A. (2008), Essentials of management, Cengage Learning
- Janik W., Paździor A. (2011), Zarządzanie finansowe w przedsiębiorstwie, Politechnika Lubelska, Lublin
- Krajewski M. (1997), Zarządzanie majątkiem obrotowym w przedsiębiorstwie, ODDK, Gdańsk
- Lucey T. (2002), Quantitative Techniques, Cengage Learning EMEA
- Pooler V. (1997), Purchasing and Supply Management: Creating the Vision, Springer Science & Business Media
- Siegel J. (2006), Accounting Handbook, Barron's Educational Series
Autor: Anna Mizia, Michał Białas