Izokwanta: Różnice pomiędzy wersjami
m (cleanup bibliografii i rotten links) |
Nie podano opisu zmian |
||
| Linia 23: | Linia 23: | ||
Poszczególne punkty na izokwancie odzwierciedlają różne metody wytwarzania takiej samej ilości produktu. Każdy punkt na izokwancie reprezentuje inną metodę wytwarzania - od metod najbardziej [[kapitał]]ochłonnych do najbardziej pracochłonnych. | Poszczególne punkty na izokwancie odzwierciedlają różne metody wytwarzania takiej samej ilości produktu. Każdy punkt na izokwancie reprezentuje inną metodę wytwarzania - od metod najbardziej [[kapitał]]ochłonnych do najbardziej pracochłonnych. | ||
Umiejscowienie kilku izokwant na wykresie pokazuje nam swoistą mapę. Każda izokwanta pokazuje różne kombinacje [[nakład]]ów wykorzystanych w | Umiejscowienie kilku izokwant na wykresie pokazuje nam swoistą mapę. Każda izokwanta pokazuje różne kombinacje [[nakład]]ów wykorzystanych w [[proces]]ie produkcji w celu wytworzenia [[dane]]j wielkości produktu. | ||
==Rodzaje Substytucji== | ==Rodzaje Substytucji== | ||
Izokwanty w zależności od kształtu krzywej możemy wyróżnić na: | Izokwanty w zależności od kształtu krzywej możemy wyróżnić na: | ||
* Substytucje pełną - jeden [[czynnik wytwórczy]] może być zastąpiony przez drugi czynnik wytwórczy. Całkowita swoboda podmieniania jednego czynnika drugim. W substytucji pełnej może wystąpić sytuacja, w której [[czynniki produkcji]] będą względem siebie znakomitymi | * Substytucje pełną - jeden [[czynnik wytwórczy]] może być zastąpiony przez drugi czynnik wytwórczy. Całkowita swoboda podmieniania jednego czynnika drugim. W substytucji pełnej może wystąpić sytuacja, w której [[czynniki produkcji]] będą względem siebie znakomitymi [[substytut]]ami. Oznacza to, że zastępowanie czynników względem siebie odbywa się w określonej proporcji, np. 1:1. W takiej sytuacji izokwanta jest opadająca krzywa liniową. Występuje również sytuacja w której [[produkcja]] może być wyrabiana przy stałym stosunku ilościowym. Taką izokwantę określamy krzywą doskonałej komplementarności. Ma ona kształt ramienia kąta prostego. | ||
* Substytucję niepełną - żaden z czynników wytwórczych nie może być całkowicie zastąpiony przez drugi czynnik wytwórczy. Krzywa nie dotyka osi współrzędnych. Im wyższy jest stopień substytucji, tym silniej krzywa będzie uwypuklać się w kierunku początku układu współrzędnych (Z.Dach, 2001, s. 139) | * Substytucję niepełną - żaden z czynników wytwórczych nie może być całkowicie zastąpiony przez drugi czynnik wytwórczy. Krzywa nie dotyka osi współrzędnych. Im wyższy jest stopień substytucji, tym silniej krzywa będzie uwypuklać się w kierunku początku układu współrzędnych (Z.Dach, 2001, s. 139) | ||
W substytucji niepełnej każdy z czynników musi być wytwarzany w określonej wielkości, żadnego z nich nie można całkowicie zastąpić. Mała swoboda podmieniania jednego czynnika drugim z powodu na brak możliwości całkowitego zrezygnowania z wytwarzania obu czynników wytwórczych. | W substytucji niepełnej każdy z czynników musi być wytwarzany w określonej wielkości, żadnego z nich nie można całkowicie zastąpić. Mała swoboda podmieniania jednego czynnika drugim z powodu na brak możliwości całkowitego zrezygnowania z wytwarzania obu czynników wytwórczych. | ||
| Linia 35: | Linia 35: | ||
* Ponieważ każda z nich odnosi się do różnej wielkości produkcji nie mogą się przecinać między sobą. | * Ponieważ każda z nich odnosi się do różnej wielkości produkcji nie mogą się przecinać między sobą. | ||
<google>ban728t</google> | <google>ban728t</google> | ||
* Wszystkie izokwanty mają nachylenie ujemne. | * Wszystkie izokwanty mają nachylenie ujemne. [[Wynik]]a to z faktu, iż każde [[przedsiębiorstwo]] dysponując ograniczonymi [[zasób|zasobami]] czynników produkcji i chcąc wytworzyć daną wielkość produkcji, rozważy zmianę technologii na bardziej kapitałochłonną tylko wówczas gdy pozwoli to na zmniejszenie nakładów pracy i na odwrót. | ||
* Poszczególne izokwanty stopniowo ulegają "spłaszczeniu" w miarę przesuwania się po nich w [[prawo]], co jest efektem angażowania coraz większej dodatkowej ilości kapitału w celu zrównoważenia kolejnych takich samych obniżek nakładów pracy potrzebnych do wytworzenia wciąż takiej samej ilości produktu (D. Begg 2003, s. 334) | * Poszczególne izokwanty stopniowo ulegają "spłaszczeniu" w miarę przesuwania się po nich w [[prawo]], co jest efektem angażowania coraz większej dodatkowej ilości kapitału w celu zrównoważenia kolejnych takich samych obniżek nakładów pracy potrzebnych do wytworzenia wciąż takiej samej ilości produktu (D. Begg 2003, s. 334) | ||
| Linia 42: | Linia 42: | ||
==Zastosowanie== | ==Zastosowanie== | ||
Izokwanta potrzebna jest Do policzenia m.in.: | Izokwanta potrzebna jest Do policzenia m.in.: | ||
* Optimum produkcji, jest to "optymalna kombinacja czynników znajduje się punkcie styczności linii jednakowego | * [[Optimum produkcji]], jest to "optymalna kombinacja czynników znajduje się punkcie styczności linii jednakowego [[koszt]]u z możliwie najwyżej położoną izokwantą produkcji. Jest to punkt równowagi przedsiębiorstwa osiągający maksymalna produkcje". (M. Rekowski 2002, s. 161) | ||
* Ścieżki ekspansji produktu, jest to "krzywa która łączy punkty styczności między izokwantami produkcji oraz równoległymi liniami jednostkowymi kosztów. Punkty te oznaczają optymalne kombinacje czynników odpowiadające różnym poziomom produkcji" (M. Rekowski 2002, s. 164) | * Ścieżki ekspansji produktu, jest to "krzywa która łączy punkty styczności między izokwantami produkcji oraz równoległymi liniami jednostkowymi kosztów. Punkty te oznaczają optymalne kombinacje czynników odpowiadające różnym poziomom produkcji" (M. Rekowski 2002, s. 164) | ||
==Zastosowanie izokwant w zarządzaniu== | |||
===Optymalna kombinacja czynników produkcji i ścieżki ekspansji produktu=== | |||
Izokwanty pozwalają na identyfikację optymalnej kombinacji czynników produkcji, czyli takiej, która minimalizuje [[koszty]] przy osiągnięciu pożądanej ilości produkcji. Dzięki analizie izokwant [[menedżer]]owie mogą określić, jakie proporcje czynników są najbardziej efektywne i jakie zmiany w alokacji zasobów mogą prowadzić do większej efektywności produkcji. Ponadto, izokwanty umożliwiają zidentyfikowanie potencjalnych ścieżek ekspansji produktu, czyli jakie kombinacje czynników są potrzebne do osiągnięcia wyższych poziomów produkcji. | |||
===Analiza efektywności produkcji i podejmowanie decyzji dotyczących alokacji zasobów=== | |||
Izokwanty pozwalają na analizę efektywności produkcji poprzez porównanie różnych kombinacji czynników produkcji. [[Menadżer]]owie mogą ocenić, jakie kombinacje czynników są bardziej wydajne i jakie zmiany w alokacji zasobów mogą prowadzić do większej efektywności. Na podstawie tych analiz mogą podejmować decyzje dotyczące alokacji zasobów, takie jak zwiększenie ilości jednego czynnika przy stałej ilości drugiego lub zwiększenie ilości obu czynników w odpowiednich proporcjach. | |||
===Zwiększanie ilości produktu na izokwantach poprzez zwiększenie ilości jednego czynnika przy stałej ilości drugiego lub zwiększenie ilości obu czynników w odpowiednich proporcjach=== | |||
Izokwanty umożliwiają menedżerom zwiększanie ilości produktu na wybranych izokwantach. Istnieją dwie główne strategie, które mogą być wykorzystane w tym celu. Pierwsza polega na zwiększeniu ilości jednego czynnika przy stałej ilości drugiego czynnika. Na przykład, jeśli jednym z czynników produkcji jest [[praca]], menedżerowie mogą zwiększyć ilość [[pracownik]]ów przy stałej ilości maszyn, co prowadzi do zwiększenia produkcji. Druga [[strategia]] polega na zwiększeniu ilości obu czynników w odpowiednich proporcjach. Na przykład, zwiększenie zarówno ilości pracowników, jak i ilości maszyn, może prowadzić do większej produkcji. | |||
===Elastyczność substytucji i jej związek z nachyleniem izokwanty=== | |||
Izokwanta przedstawia kombinacje czynników produkcji, które umożliwiają osiągnięcie tej samej ilości produkcji. Nachylenie izokwanty odzwierciedla elastyczność substytucji między czynnikami produkcji. Im bardziej strome jest nachylenie izokwanty, tym mniejsza jest elastyczność substytucji między czynnikami. Z kolei im bardziej płaskie jest nachylenie izokwanty, tym większa jest elastyczność substytucji. Ta [[informacja]] jest niezwykle cenna dla menedżerów, ponieważ pozwala na ocenę, jak zmiany w alokacji zasobów wpływają na produkcję. | |||
===Analiza skalowania produkcji i konkurencji na rynku przy wykorzystaniu izokwant=== | |||
Izokwanty pozwalają na analizę skalowania produkcji, czyli jak zmiany w wielkości produkcji wpływają na koszty. Menedżerowie mogą ocenić, czy zwiększenie skali produkcji prowadzi do zmniejszenia kosztów jednostkowych czy też nie. Ponadto, izokwanty umożliwiają analizę konkurencji na rynku. Porównując izokwanty różnych firm, menedżerowie mogą ocenić, jakie kombinacje czynników produkcji są wykorzystywane przez konkurencję i jaką ilość produktu są w stanie wyprodukować. Ta [[wiedza]] może być wykorzystana do opracowania strategii konkurencyjnych. | |||
===Uwzględnienie aspektów ekologicznych i prognozowanie przyszłej produkcji na podstawie analizy izokwant=== | |||
Analiza izokwant może być również wykorzystana do uwzględnienia aspektów ekologicznych w [[zarząd]]zaniu. Izokwanty pozwalają na ocenę, jakie kombinacje czynników produkcji są bardziej przyjazne dla środowiska. Menedżerowie mogą wykorzystać tę wiedzę do podejmowania decyzji dotyczących ograniczenia negatywnego wpływu produkcji na środowisko. Ponadto, analiza izokwant umożliwia [[prognozowanie]] przyszłej produkcji na podstawie obecnych danych. Menedżerowie mogą przewidywać, jakie ilości produktu mogą być osiągnięte w przyszłości na podstawie kombinacji czynników produkcji i istniejących izokwant. | |||
===Wykorzystanie programowania liniowego i metody matematycznego programowania w analizie izokwant=== | |||
[[Program]]owanie liniowe i [[metoda]] matematycznego programowania są narzędziami, które można wykorzystać do analizy izokwant. [[Programowanie]] liniowe pozwala na optymalizację produkcji, czyli znalezienie najbardziej efektywnego zestawu czynników produkcji, który zapewni maksymalną wielkość produkcji przy określonych ograniczeniach. | |||
W kontekście izokwant, [[programowanie liniowe]] może być wykorzystane do znalezienia optymalnego poziomu ilości czynników produkcji, który zapewni osiągnięcie określonej wielkości produkcji. Przykładowo, jeśli chcemy osiągnąć produkcję na poziomie Q =jednostek, programowanie liniowe pozwoli nam znaleźć optymalne wartości ilości czynników produkcji, które będą to umożliwiać. | |||
Metoda matematycznego programowania, która wykorzystuje programowanie liniowe, jest również przydatna w analizie izokwant. Pozwala ona na uwzględnienie różnych czynników produkcji oraz ich wzajemnych zależności, co może prowadzić do bardziej realistycznego [[model]]u izokwant. | |||
===Metoda ekonometryczna jako narzędzie analizy statystycznej zależności między czynnikami produkcji a wielkością produkcji=== | |||
Metoda [[ekonom]]etryczna jest narzędziem analizy statystycznej, które można wykorzystać do badania zależności między czynnikami produkcji a wielkością produkcji. Metoda ta pozwala na ocenę wpływu poszczególnych czynników produkcji na wielkość produkcji oraz na identyfikację istotnych czynników determinujących produkcję. | |||
W kontekście izokwant, metoda ekonometryczna może być wykorzystana do oszacowania [[parametr]]ów funkcji produkcji. Poprzez analizę dostępnych danych dotyczących ilości czynników produkcji i wielkości produkcji, możemy estymować parametry takich modeli, jak [[funkcja]] Cobb-Douglasa, funkcja Leontieffa czy funkcja CES. | |||
Metoda ekonometryczna obejmuje różne techniki, takie jak [[regres]]ja liniowa, [[regresja]] logistyczna czy analiza szeregów czasowych. Wybór konkretnej metody zależy od charakteru badanych danych oraz celu analizy. | |||
===Wykorzystanie map izokwant, wykresów izokwant i diagramów izokwant w graficznym przedstawianiu izokwant=== | |||
Mapy izokwant, wykresy izokwant i diagramy izokwant są graficznymi narzędziami, które można wykorzystać do przedstawienia izokwant. Izokwanty są krzywymi, które pokazują różne poziomy produkcji osiągane przy różnych kombinacjach ilości czynników produkcji. | |||
Mapy izokwant są szczególnie przydatne w analizie izokwant, ponieważ pozwalają na przedstawienie izokwant w przestrzeni dwuwymiarowej, gdzie każda oś odpowiada jednemu z czynników produkcji. Na mapie izokwant możemy zobaczyć, jak [[zmiana]] ilości jednego czynnika produkcji wpływa na wielkość produkcji. | |||
Wykresy izokwant, z drugiej strony, pozwalają na przedstawienie izokwant w przestrzeni jednowymiarowej. Wykresy te są szczególnie przydatne, gdy analizujemy zależność między dwoma czynnikami produkcji. | |||
Diagramy izokwant są jeszcze innym sposobem graficznego przedstawiania izokwant. W diagramach izokwant można zobaczyć, jak różne izokwanty przecinają się i jak zmieniają się w zależności od ilości czynników produkcji. | |||
Wykorzystanie map izokwant, wykresów izokwant i diagramów izokwant w analizie izokwant pozwala na lepsze zrozumienie zależności między czynnikami produkcji a wielkością produkcji. Graficzne przedstawienie izokwant jest często bardziej czytelne i łatwiejsze do interpretacji niż same liczby i równania. | |||
===Wykorzystanie programów komputerowych do analizy izokwant=== | |||
Wraz z postępem technologicznym, analiza izokwant stała się bardziej precyzyjna i skuteczna dzięki wykorzystaniu programów komputerowych. Dzięki nim możliwe jest generowanie wykresów izokwant oraz przeprowadzanie bardziej zaawansowanych obliczeń. | |||
Programy komputerowe pozwalają na szybkie i łatwe tworzenie izokwant na podstawie danych dotyczących produkcji i kosztów. Dzięki temu można dokładnie przedstawić różne kombinacje czynników produkcji i określić ich wpływ na produkcję oraz koszty. | |||
Dodatkowo, programy komputerowe umożliwiają również przeprowadzanie analizy wrażliwości. Dzięki temu można ocenić, jak zmiany w jednym z czynników produkcji wpływają na inne czynniki oraz na wyniki produkcyjne i koszty. | |||
Wykorzystanie programów komputerowych do analizy izokwant znacznie ułatwia i przyspiesza proces analizy. Pozwala również na bardziej zaawansowane i dokładne badania, które mogą prowadzić do optymalizacji procesów produkcyjnych. | |||
===Metoda elastyczności substytucji i jej zastosowanie w analizie izokwant=== | |||
Metoda elastyczności substytucji jest narzędziem stosowanym w analizie izokwant, pozwalającym ocenić stopień zastępowalności jednego czynnika produkcji przez inny. Oznacza to, że metoda ta umożliwia określenie, jak zmiana ilości jednego czynnika wpływa na zmianę ilości drugiego czynnika, aby utrzymać tę samą produkcję. | |||
Wykorzystanie metody elastyczności substytucji w analizie izokwant pozwala na dokładniejsze zrozumienie relacji pomiędzy różnymi czynnikami produkcji. Dzięki tej metodzie można ocenić, które czynniki są bardziej elastyczne i mogą być łatwo zastąpione innymi, a które są mniej elastyczne i mają większy wpływ na [[proces produkcyjny]]. | |||
Metoda elastyczności substytucji może być również używana do prognozowania zmian w czynnikach produkcji oraz do oceny wpływu zmian w [[cena]]ch czynników na proces produkcyjny. Dzięki temu można podejmować lepsze decyzje dotyczące alokacji zasobów i optymalizować [[koszty produkcji]]. | |||
===Metoda analizy kosztów produkcji jako narzędzie oceny opłacalności różnych kombinacji czynników produkcji=== | |||
Metoda analizy kosztów produkcji jest jednym z narzędzi stosowanych w analizie izokwant, pozwalającym na ocenę opłacalności różnych kombinacji czynników produkcji. Polega ona na porównaniu kosztów produkcji dla różnych kombinacji czynników i określeniu, która z nich jest najbardziej efektywna ekonomicznie. | |||
Analiza kosztów produkcji pozwala na identyfikację optymalnej kombinacji czynników produkcji, która minimalizuje koszty przy określonym poziomie produkcji. Dzięki tej metodzie można dokładnie ustalić, jakie czynniki mają największy wpływ na koszty produkcji i jak można je zoptymalizować. | |||
Metoda analizy kosztów produkcji jest szczególnie przydatna dla przedsiębiorstw, które chcą zminimalizować swoje koszty i zwiększyć swoją [[rentowność]]. Pozwala ona również na ocenę skutków różnych decyzji dotyczących alokacji zasobów oraz wprowadzania nowych technologii i procesów produkcyjnych. | |||
==Bibliografia== | ==Bibliografia== | ||
Wersja z 14:56, 16 lis 2023
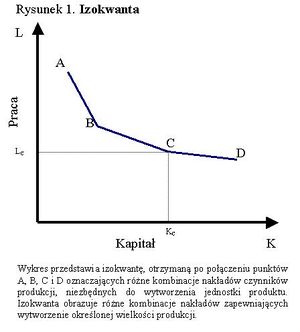
Izokwanta (krzywa jednakowego produktu) jest zbiorem możliwych kombinacji nakładu dwóch czynników produkcji, które pozwalają efektywnie wytworzyć daną wielkość produktu.
Izokwanty swym wyglądem przypominają krzywe obojętności. Istnieje jednak zasadnicza różnica między nimi, gdyż izokwanty są oznaczone ilością produktu, jaka im odpowiada, a nie poziomami użyteczności jak jest w przypadku krzywych obojętności (H. R. Varian, 2002, s. 339)
Interpretacja
Poszczególne punkty na izokwancie odzwierciedlają różne metody wytwarzania takiej samej ilości produktu. Każdy punkt na izokwancie reprezentuje inną metodę wytwarzania - od metod najbardziej kapitałochłonnych do najbardziej pracochłonnych.
Umiejscowienie kilku izokwant na wykresie pokazuje nam swoistą mapę. Każda izokwanta pokazuje różne kombinacje nakładów wykorzystanych w procesie produkcji w celu wytworzenia danej wielkości produktu.
Rodzaje Substytucji
Izokwanty w zależności od kształtu krzywej możemy wyróżnić na:
- Substytucje pełną - jeden czynnik wytwórczy może być zastąpiony przez drugi czynnik wytwórczy. Całkowita swoboda podmieniania jednego czynnika drugim. W substytucji pełnej może wystąpić sytuacja, w której czynniki produkcji będą względem siebie znakomitymi substytutami. Oznacza to, że zastępowanie czynników względem siebie odbywa się w określonej proporcji, np. 1:1. W takiej sytuacji izokwanta jest opadająca krzywa liniową. Występuje również sytuacja w której produkcja może być wyrabiana przy stałym stosunku ilościowym. Taką izokwantę określamy krzywą doskonałej komplementarności. Ma ona kształt ramienia kąta prostego.
- Substytucję niepełną - żaden z czynników wytwórczych nie może być całkowicie zastąpiony przez drugi czynnik wytwórczy. Krzywa nie dotyka osi współrzędnych. Im wyższy jest stopień substytucji, tym silniej krzywa będzie uwypuklać się w kierunku początku układu współrzędnych (Z.Dach, 2001, s. 139)
W substytucji niepełnej każdy z czynników musi być wytwarzany w określonej wielkości, żadnego z nich nie można całkowicie zastąpić. Mała swoboda podmieniania jednego czynnika drugim z powodu na brak możliwości całkowitego zrezygnowania z wytwarzania obu czynników wytwórczych.
Cechy
Izokwanty charakteryzują się trzema cechami:
- Ponieważ każda z nich odnosi się do różnej wielkości produkcji nie mogą się przecinać między sobą.
- Wszystkie izokwanty mają nachylenie ujemne. Wynika to z faktu, iż każde przedsiębiorstwo dysponując ograniczonymi zasobami czynników produkcji i chcąc wytworzyć daną wielkość produkcji, rozważy zmianę technologii na bardziej kapitałochłonną tylko wówczas gdy pozwoli to na zmniejszenie nakładów pracy i na odwrót.
- Poszczególne izokwanty stopniowo ulegają "spłaszczeniu" w miarę przesuwania się po nich w prawo, co jest efektem angażowania coraz większej dodatkowej ilości kapitału w celu zrównoważenia kolejnych takich samych obniżek nakładów pracy potrzebnych do wytworzenia wciąż takiej samej ilości produktu (D. Begg 2003, s. 334)
Podsumowując izokwanta jest to geometryczne miejsce takich ilościowych kombinacji czynników produkcji, które zapewniają jednakowy poziom produkcji (produktu). (A. Becla 2001, s. 151)
Zastosowanie
Izokwanta potrzebna jest Do policzenia m.in.:
- Optimum produkcji, jest to "optymalna kombinacja czynników znajduje się punkcie styczności linii jednakowego kosztu z możliwie najwyżej położoną izokwantą produkcji. Jest to punkt równowagi przedsiębiorstwa osiągający maksymalna produkcje". (M. Rekowski 2002, s. 161)
- Ścieżki ekspansji produktu, jest to "krzywa która łączy punkty styczności między izokwantami produkcji oraz równoległymi liniami jednostkowymi kosztów. Punkty te oznaczają optymalne kombinacje czynników odpowiadające różnym poziomom produkcji" (M. Rekowski 2002, s. 164)
Zastosowanie izokwant w zarządzaniu
Optymalna kombinacja czynników produkcji i ścieżki ekspansji produktu
Izokwanty pozwalają na identyfikację optymalnej kombinacji czynników produkcji, czyli takiej, która minimalizuje koszty przy osiągnięciu pożądanej ilości produkcji. Dzięki analizie izokwant menedżerowie mogą określić, jakie proporcje czynników są najbardziej efektywne i jakie zmiany w alokacji zasobów mogą prowadzić do większej efektywności produkcji. Ponadto, izokwanty umożliwiają zidentyfikowanie potencjalnych ścieżek ekspansji produktu, czyli jakie kombinacje czynników są potrzebne do osiągnięcia wyższych poziomów produkcji.
Analiza efektywności produkcji i podejmowanie decyzji dotyczących alokacji zasobów
Izokwanty pozwalają na analizę efektywności produkcji poprzez porównanie różnych kombinacji czynników produkcji. Menadżerowie mogą ocenić, jakie kombinacje czynników są bardziej wydajne i jakie zmiany w alokacji zasobów mogą prowadzić do większej efektywności. Na podstawie tych analiz mogą podejmować decyzje dotyczące alokacji zasobów, takie jak zwiększenie ilości jednego czynnika przy stałej ilości drugiego lub zwiększenie ilości obu czynników w odpowiednich proporcjach.
Zwiększanie ilości produktu na izokwantach poprzez zwiększenie ilości jednego czynnika przy stałej ilości drugiego lub zwiększenie ilości obu czynników w odpowiednich proporcjach
Izokwanty umożliwiają menedżerom zwiększanie ilości produktu na wybranych izokwantach. Istnieją dwie główne strategie, które mogą być wykorzystane w tym celu. Pierwsza polega na zwiększeniu ilości jednego czynnika przy stałej ilości drugiego czynnika. Na przykład, jeśli jednym z czynników produkcji jest praca, menedżerowie mogą zwiększyć ilość pracowników przy stałej ilości maszyn, co prowadzi do zwiększenia produkcji. Druga strategia polega na zwiększeniu ilości obu czynników w odpowiednich proporcjach. Na przykład, zwiększenie zarówno ilości pracowników, jak i ilości maszyn, może prowadzić do większej produkcji.
Elastyczność substytucji i jej związek z nachyleniem izokwanty
Izokwanta przedstawia kombinacje czynników produkcji, które umożliwiają osiągnięcie tej samej ilości produkcji. Nachylenie izokwanty odzwierciedla elastyczność substytucji między czynnikami produkcji. Im bardziej strome jest nachylenie izokwanty, tym mniejsza jest elastyczność substytucji między czynnikami. Z kolei im bardziej płaskie jest nachylenie izokwanty, tym większa jest elastyczność substytucji. Ta informacja jest niezwykle cenna dla menedżerów, ponieważ pozwala na ocenę, jak zmiany w alokacji zasobów wpływają na produkcję.
Analiza skalowania produkcji i konkurencji na rynku przy wykorzystaniu izokwant
Izokwanty pozwalają na analizę skalowania produkcji, czyli jak zmiany w wielkości produkcji wpływają na koszty. Menedżerowie mogą ocenić, czy zwiększenie skali produkcji prowadzi do zmniejszenia kosztów jednostkowych czy też nie. Ponadto, izokwanty umożliwiają analizę konkurencji na rynku. Porównując izokwanty różnych firm, menedżerowie mogą ocenić, jakie kombinacje czynników produkcji są wykorzystywane przez konkurencję i jaką ilość produktu są w stanie wyprodukować. Ta wiedza może być wykorzystana do opracowania strategii konkurencyjnych.
Uwzględnienie aspektów ekologicznych i prognozowanie przyszłej produkcji na podstawie analizy izokwant
Analiza izokwant może być również wykorzystana do uwzględnienia aspektów ekologicznych w zarządzaniu. Izokwanty pozwalają na ocenę, jakie kombinacje czynników produkcji są bardziej przyjazne dla środowiska. Menedżerowie mogą wykorzystać tę wiedzę do podejmowania decyzji dotyczących ograniczenia negatywnego wpływu produkcji na środowisko. Ponadto, analiza izokwant umożliwia prognozowanie przyszłej produkcji na podstawie obecnych danych. Menedżerowie mogą przewidywać, jakie ilości produktu mogą być osiągnięte w przyszłości na podstawie kombinacji czynników produkcji i istniejących izokwant.
Wykorzystanie programowania liniowego i metody matematycznego programowania w analizie izokwant
Programowanie liniowe i metoda matematycznego programowania są narzędziami, które można wykorzystać do analizy izokwant. Programowanie liniowe pozwala na optymalizację produkcji, czyli znalezienie najbardziej efektywnego zestawu czynników produkcji, który zapewni maksymalną wielkość produkcji przy określonych ograniczeniach.
W kontekście izokwant, programowanie liniowe może być wykorzystane do znalezienia optymalnego poziomu ilości czynników produkcji, który zapewni osiągnięcie określonej wielkości produkcji. Przykładowo, jeśli chcemy osiągnąć produkcję na poziomie Q =jednostek, programowanie liniowe pozwoli nam znaleźć optymalne wartości ilości czynników produkcji, które będą to umożliwiać.
Metoda matematycznego programowania, która wykorzystuje programowanie liniowe, jest również przydatna w analizie izokwant. Pozwala ona na uwzględnienie różnych czynników produkcji oraz ich wzajemnych zależności, co może prowadzić do bardziej realistycznego modelu izokwant.
Metoda ekonometryczna jako narzędzie analizy statystycznej zależności między czynnikami produkcji a wielkością produkcji
Metoda ekonometryczna jest narzędziem analizy statystycznej, które można wykorzystać do badania zależności między czynnikami produkcji a wielkością produkcji. Metoda ta pozwala na ocenę wpływu poszczególnych czynników produkcji na wielkość produkcji oraz na identyfikację istotnych czynników determinujących produkcję.
W kontekście izokwant, metoda ekonometryczna może być wykorzystana do oszacowania parametrów funkcji produkcji. Poprzez analizę dostępnych danych dotyczących ilości czynników produkcji i wielkości produkcji, możemy estymować parametry takich modeli, jak funkcja Cobb-Douglasa, funkcja Leontieffa czy funkcja CES.
Metoda ekonometryczna obejmuje różne techniki, takie jak regresja liniowa, regresja logistyczna czy analiza szeregów czasowych. Wybór konkretnej metody zależy od charakteru badanych danych oraz celu analizy.
Wykorzystanie map izokwant, wykresów izokwant i diagramów izokwant w graficznym przedstawianiu izokwant
Mapy izokwant, wykresy izokwant i diagramy izokwant są graficznymi narzędziami, które można wykorzystać do przedstawienia izokwant. Izokwanty są krzywymi, które pokazują różne poziomy produkcji osiągane przy różnych kombinacjach ilości czynników produkcji.
Mapy izokwant są szczególnie przydatne w analizie izokwant, ponieważ pozwalają na przedstawienie izokwant w przestrzeni dwuwymiarowej, gdzie każda oś odpowiada jednemu z czynników produkcji. Na mapie izokwant możemy zobaczyć, jak zmiana ilości jednego czynnika produkcji wpływa na wielkość produkcji.
Wykresy izokwant, z drugiej strony, pozwalają na przedstawienie izokwant w przestrzeni jednowymiarowej. Wykresy te są szczególnie przydatne, gdy analizujemy zależność między dwoma czynnikami produkcji.
Diagramy izokwant są jeszcze innym sposobem graficznego przedstawiania izokwant. W diagramach izokwant można zobaczyć, jak różne izokwanty przecinają się i jak zmieniają się w zależności od ilości czynników produkcji.
Wykorzystanie map izokwant, wykresów izokwant i diagramów izokwant w analizie izokwant pozwala na lepsze zrozumienie zależności między czynnikami produkcji a wielkością produkcji. Graficzne przedstawienie izokwant jest często bardziej czytelne i łatwiejsze do interpretacji niż same liczby i równania.
Wykorzystanie programów komputerowych do analizy izokwant
Wraz z postępem technologicznym, analiza izokwant stała się bardziej precyzyjna i skuteczna dzięki wykorzystaniu programów komputerowych. Dzięki nim możliwe jest generowanie wykresów izokwant oraz przeprowadzanie bardziej zaawansowanych obliczeń.
Programy komputerowe pozwalają na szybkie i łatwe tworzenie izokwant na podstawie danych dotyczących produkcji i kosztów. Dzięki temu można dokładnie przedstawić różne kombinacje czynników produkcji i określić ich wpływ na produkcję oraz koszty.
Dodatkowo, programy komputerowe umożliwiają również przeprowadzanie analizy wrażliwości. Dzięki temu można ocenić, jak zmiany w jednym z czynników produkcji wpływają na inne czynniki oraz na wyniki produkcyjne i koszty.
Wykorzystanie programów komputerowych do analizy izokwant znacznie ułatwia i przyspiesza proces analizy. Pozwala również na bardziej zaawansowane i dokładne badania, które mogą prowadzić do optymalizacji procesów produkcyjnych.
Metoda elastyczności substytucji i jej zastosowanie w analizie izokwant
Metoda elastyczności substytucji jest narzędziem stosowanym w analizie izokwant, pozwalającym ocenić stopień zastępowalności jednego czynnika produkcji przez inny. Oznacza to, że metoda ta umożliwia określenie, jak zmiana ilości jednego czynnika wpływa na zmianę ilości drugiego czynnika, aby utrzymać tę samą produkcję.
Wykorzystanie metody elastyczności substytucji w analizie izokwant pozwala na dokładniejsze zrozumienie relacji pomiędzy różnymi czynnikami produkcji. Dzięki tej metodzie można ocenić, które czynniki są bardziej elastyczne i mogą być łatwo zastąpione innymi, a które są mniej elastyczne i mają większy wpływ na proces produkcyjny.
Metoda elastyczności substytucji może być również używana do prognozowania zmian w czynnikach produkcji oraz do oceny wpływu zmian w cenach czynników na proces produkcyjny. Dzięki temu można podejmować lepsze decyzje dotyczące alokacji zasobów i optymalizować koszty produkcji.
Metoda analizy kosztów produkcji jako narzędzie oceny opłacalności różnych kombinacji czynników produkcji
Metoda analizy kosztów produkcji jest jednym z narzędzi stosowanych w analizie izokwant, pozwalającym na ocenę opłacalności różnych kombinacji czynników produkcji. Polega ona na porównaniu kosztów produkcji dla różnych kombinacji czynników i określeniu, która z nich jest najbardziej efektywna ekonomicznie.
Analiza kosztów produkcji pozwala na identyfikację optymalnej kombinacji czynników produkcji, która minimalizuje koszty przy określonym poziomie produkcji. Dzięki tej metodzie można dokładnie ustalić, jakie czynniki mają największy wpływ na koszty produkcji i jak można je zoptymalizować.
Metoda analizy kosztów produkcji jest szczególnie przydatna dla przedsiębiorstw, które chcą zminimalizować swoje koszty i zwiększyć swoją rentowność. Pozwala ona również na ocenę skutków różnych decyzji dotyczących alokacji zasobów oraz wprowadzania nowych technologii i procesów produkcyjnych.
Bibliografia
- Becla A., Czaja S., Hałasa J. M., Rumianowska I. (2001), Elementy Mikroekonomii, Wydawnictwo I-BiS, Wrocław
- Begg D., Fisher S., Vernasca G., Dornbusch R. (2014), Ekonomia: Makroekonomia, Polskie Wydawnictwo Ekonomiczne, Warszawa
- Dach Z. (2001), Podstawy mikroekonomii, Wydawnictwo Naukowe SYNABA, Kraków
- Nojszewska E. (2015),Ekonomiczna analiza efektywności szpitaliMyśl Ekonomiczna i Polityczna, nr.2
- Rekowski M. (2002), Wprowadzenie do mikroekonomii, Wydawnictwo AE, Poznań
- Varian H. (2013), Mikroekonomia. Kurs średni - ujęcie nowoczesne, Wydawnictwo Naukowe PWN, Warszawa
- Zalega T. (2015), Mikroekonomia współczesna, Wydawnictwo Naukowe Wydziału Zarządzania Uniwersytetu Warszawskiego, Warszawa
Autor: Kamil Czerwonka i Robert Dzień