Próg rentowności

Próg rentowności
Polecane artykuły
Margines bezpieczeństwa Kalkulacja cen na podstawie kosztu jednostkowego NPV Dochodowe metody wyceny przedsiębiorstw Wskaźnik rentowności Średni ważony koszt kapitału Zysk operacyjny Błąd względny Analiza Du Ponta

Próg rentowności (BEP - break even point) – to punkt graniczny, w którym badane przedsięwzięcie nie przynosi zysków ani nie powoduje strat. W punkcie tym następuje zrównanie przychodów z całkowitymi kosztami poniesionymi przez przedsiębiorstwo. Wynik finansowy wynosi zero.

Próg rentowności jest przydatny w bieżącym zarządzaniu przedsiębiorstwem. Wykorzystywany jest również do oceny projektów inwestycyjnych.

Próg rentowności może być wyrażony:

• ilościowo - ilość produkcji, przy której BEP jest równy zero
• wartościowo - wartość produkcji, przy której BEP jest równy zero, gdzie wartość przychodów ze sprzedaży równa się kosztom całkowitym
• procentowo – określający jaką część przewidywanego popytu należy wykorzystać by poniesione koszty zrównoważyć przychodami ze sprzedaży

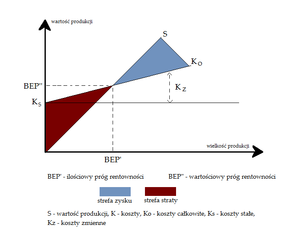
Próg rentowności można również przedstawić w sposób graficzny.

Rys. 1 Próg rentowności

Próg rentowności można obliczyć jako relację kosztów stałych przedsiębiorstwa do stopy marży pokrycia. W analizie progu rentowności ustala się marże bezpieczeństwa (bezwzględną i względną) pokazujące, o ile można obniżyć sprzedaż (wartościowo i procentowo), aby nie ponieść strat.

Analiza progu rentowności opiera się na podziale ogółu kosztów ponoszonych przez przedsiębiorstwo na koszty stałe - niezależnych od wielkości produkcji - oraz zmienne - zależne od kosztów produkcji. Przyjmuje się pewne założenia upraszczające, co do poziomu ceny i kosztów w okresie obliczania.

TL;DR

Próg rentowności to punkt graniczny, w którym przedsięwzięcie nie przynosi zysków ani nie powoduje strat. Może być wyrażony ilościowo, wartościowo lub procentowo. Oblicza się go jako relację kosztów stałych do stopy marży pokrycia. Może być rozszerzony o koszty finansowe. Analiza progu rentowności w ujęciu prospektywnym uwzględnia niepewność dotyczącą przyjętych wartości. Wyznacza się także prawdopodobieństwo osiągnięcia progu rentowności.

Ilościowy próg rentowności

{{#ev:youtube|Q1qALh51ijw|480|right|Opłacalność projektu (Sławomir Wawak)|frame}} Ogólny wzór na obliczenie ilościowego progu rentowności przedstawia się następująco:

Parser nie mógł rozpoznać (SVG (MathML może zostać włączone przez wtyczkę w przeglądarce): Nieprawidłowa odpowiedź („Math extension cannot connect to Restbase.”) z serwera „https://wikimedia.org/api/rest_v1/”:): {\displaystyle BEP ilościowy = \frac{Ks}{(Cj - Kzj)}}

Ks - całkowite koszty stałe,

Cj - cena jednostkowa,

Kzj - koszt zmienny jednostkowy,

Cj - Kzj - marża jednostkowa na pokrycie

Wartościowy próg rentowności

BEP wartościowy oblicza się natomiast mnożąc BEP ilościowy przez jednostkową cenę sprzedaży.

Parser nie mógł rozpoznać (błąd składni): {\displaystyle BEP wartościowy = BEPilościowy * Cj}

Procentowy próg rentowności

Wzór na obliczenie procentowego progu rentowności przedstawia się następująco:

$BEPprocentowy={\frac {BEP}{Xm}}*100\%$

Xm – maksymalna możliwa wielkość sprzedaży określona na podstawie prognozy popytu

Rozszerzony próg rentowności

Próg rentowności można rozszerzyć o koszty finansowe, ponieważ większość przedsiębiorstw finansuje swoją działalność kapitałami obcymi. Stanowią one ważną część całości kosztów przedsiębiorstwa. Zatem przedsiębiorstwo będzie rentowne, gdy przychody pokryją nie tylko koszty stałe i zmienne, ale również finansowe.

Wzór na próg rentowności powiększony o koszty finansowe przedstawia się następująco: $BEProzszerzony={\frac {Ks+Kf}{Cj-Kzj}}$

Kf - koszty finansowe

Analiza prospektywna progu rentowności

Analiza progu rentowności w ujęciu prospektywnym wiąże się z niepewnością, co do przyjętych w obliczeniach wartości. Największą niepewnością obarczona jest wielkość sprzedaży.

Szacowanie wartości BEP

Przeprowadzając analizę BEP w warunkach niepewności założymy, że wielkość sprzedaży ma rozkład normalny a średnia wartość sprzedaży oraz odchylenie standardowe są znane, produkcja jest jednorodna. Wartości te można oszacować na podstawie danych empirycznych z przeszłości. Można to zapisać w następujący sposób:

Q ~ N (mQ, sQ)

mQ - średnia wielkość sprzedaży,

sQ - odchylenie standardowe wielkości sprzedaży

W związku z założeniem rozkładu normalnego wynik finansowy sprzedaży będzie miał postać.

Z ~ N (mZ, sZ)

mZ - średnia wyniku finansowego

sZ - odchylenie standardowe

Można więc zapisać, że wynik finansowy sprzedaży ma następujący rozkład:

Z ~ N [(p - kQ) mQ -KS; (p - kZ) SQ]

Średnia wartość wyniku finansowego jest funkcją średniej wielkości sprzedaży, a odchylenie standardowe wyniku finansowego zależy od odchylenia standardowego wielkości sprzedaży.

Prawdopodobieństwo osiągnięcia BEP

Kolejnym krokiem jest wyznaczenie prawdopodobieństwa osiągnięcia obliczonego progu rentowności, w tym celu trzeba najpierw dokonać standaryzacji wyniku finansowego, dokonać tego można korzystając ze wzoru:

$To={\frac {(Zo-mz)}{Sz}}$

Zo - rozpatrywany poziom wyniku finansowego

To - zestandaryzowana wartość wyniku finansowego

Wartość ta wskazuje ile odchyleń standardowych wyniku finansowego stanowi różnica między założonym poziomem zysku ZO a jego wartością średnią mZ.

Wynik finansowy dla progu rentowności wynosi zero, a więc wartość zestandaryzowana tego wyniku będzie wynosiła:

$To={\frac {(0-mz)}{Sz}}=-\left({\frac {mz}{Sz}}\right)$

Na podstawie dotychczasowych obliczeń, a konkretnie założonego poziomu wyniku finansowego i jego wartości zestandaryzowanej, można wyznaczyć dwa rodzaje prawdopodobieństwa:

• prawdopodobieństwa osiągnięcia wyniku finansowego mniejszego bądź równego względem ustalonego poziomu Z0, jako wartość dystrybuanty rozkładu normalnego w punkcie T0.

P (Z<=Zo)=F (To)

• prawdopodobieństwo osiągnięcia wyniku finansowego większego niż założony poziom Z0, jako dopełnienie poprzedniego wzoru do jedności.

P (Z>Zo)=1-F (To)

Analiza ta dostarcza informacji, co do realności osiągnięcia obliczonego progu rentowności.

Bibliografia

• Nowak E. (2003) Zaawansowana rachunkowość zarządcza, PWE, Warszawa
• Sierpińska M., Jachna T. (2006). Ocena przedsiębiorstwa według standardów światowych, PWN, Warszawa
• Sobańska I. (2010). Rachunkowość zarządcza. Podejście operacyjne i strategiczne, Wydawnictwo C.H.Beck, Warszawa, s. 206-210
• Sojak S. (2012). Analiza progu rentowności, Rachunkowość, nr 10, s. 2 - 12
• Nowak E. (2005) Analiza sprawozdań finansowych, PWE, Warszawa
• Żwirbla A. (2014). Nowa metoda analizy progu rentowności oraz dźwigni ekonomicznych, Zeszyty Naukowe WSHE, Tom XXXIX, s. 87

Autor: Piotr Byrski, Karolina Kruszczak