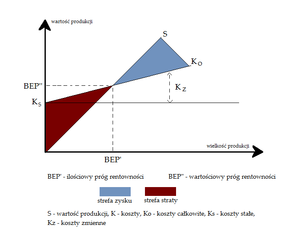
Próg rentowności
Próg rentowności (BEP - break even point) - to punkt graniczny, w którym badane przedsięwzięcie nie przynosi zysków ani nie powoduje strat. W punkcie tym następuje zrównanie przychodów z całkowitymi kosztami poniesionymi przez przedsiębiorstwo. Wynik finansowy wynosi zero.
Próg rentowności jest przydatny w bieżącym zarządzaniu przedsiębiorstwem. Wykorzystywany jest również do oceny projektów inwestycyjnych.
Próg rentowności może być wyrażony:
- ilościowo - ilość produkcji, przy której BEP jest równy zero
- wartościowo - wartość produkcji, przy której BEP jest równy zero, gdzie wartość przychodów ze sprzedaży równa się kosztom całkowitym
- procentowo - określający jaką część przewidywanego popytu należy wykorzystać by poniesione koszty zrównoważyć przychodami ze sprzedaży
Próg rentowności można również przedstawić w sposób graficzny.
Próg rentowności można obliczyć jako relację kosztów stałych przedsiębiorstwa do stopy marży pokrycia. W analizie progu rentowności ustala się marże bezpieczeństwa (bezwzględną i względną) pokazujące, o ile można obniżyć sprzedaż (wartościowo i procentowo), aby nie ponieść strat.
Analiza progu rentowności opiera się na podziale ogółu kosztów ponoszonych przez przedsiębiorstwo na koszty stałe - niezależnych od wielkości produkcji - oraz zmienne - zależne od kosztów produkcji. Przyjmuje się pewne założenia upraszczające, co do poziomu ceny i kosztów w okresie obliczania.
TL;DR
Próg rentowności to punkt graniczny, w którym przedsięwzięcie nie przynosi zysków ani nie powoduje strat. Może być wyrażony ilościowo, wartościowo lub procentowo. Oblicza się go jako relację kosztów stałych do stopy marży pokrycia. Może być rozszerzony o koszty finansowe. Analiza progu rentowności w ujęciu prospektywnym uwzględnia niepewność dotyczącą przyjętych wartości. Wyznacza się także prawdopodobieństwo osiągnięcia progu rentowności.
Ilościowy próg rentowności
Ogólny wzór na obliczenie ilościowego progu rentowności przedstawia się następująco:
- Ks - całkowite koszty stałe,
- Cj - cena jednostkowa,
- Kzj - koszt zmienny jednostkowy,
- Cj - Kzj - marża jednostkowa na pokrycie
Wartościowy próg rentowności
BEP wartościowy oblicza się natomiast mnożąc BEP ilościowy przez jednostkową cenę sprzedaży.
Procentowy próg rentowności
Wzór na obliczenie procentowego progu rentowności przedstawia się następująco:
- Xm - maksymalna możliwa wielkość sprzedaży określona na podstawie prognozy popytu
Rozszerzony próg rentowności
Próg rentowności można rozszerzyć o koszty finansowe, ponieważ większość przedsiębiorstw finansuje swoją działalność kapitałami obcymi. Stanowią one ważną część całości kosztów przedsiębiorstwa. Zatem przedsiębiorstwo będzie rentowne, gdy przychody pokryją nie tylko koszty stałe i zmienne, ale również finansowe.
Wzór na próg rentowności powiększony o koszty finansowe przedstawia się następująco:
- Kf - koszty finansowe
Analiza prospektywna progu rentowności
Analiza progu rentowności w ujęciu prospektywnym wiąże się z niepewnością, co do przyjętych w obliczeniach wartości. Największą niepewnością obarczona jest wielkość sprzedaży.
Szacowanie wartości BEP
Przeprowadzając analizę BEP w warunkach niepewności założymy, że wielkość sprzedaży ma rozkład normalny a średnia wartość sprzedaży oraz odchylenie standardowe są znane, produkcja jest jednorodna. Wartości te można oszacować na podstawie danych empirycznych z przeszłości. Można to zapisać w następujący sposób:
Q ~ N (mQ, sQ)
mQ - średnia wielkość sprzedaży,
sQ - odchylenie standardowe wielkości sprzedaży
W związku z założeniem rozkładu normalnego wynik finansowy sprzedaży będzie miał postać.
Z ~ N (mZ, sZ)
mZ - średnia wyniku finansowego
sZ - odchylenie standardowe
Można więc zapisać, że wynik finansowy sprzedaży ma następujący rozkład:
Z ~ N [(p - kQ) mQ - KS; (p - kZ) SQ]
Średnia wartość wyniku finansowego jest funkcją średniej wielkości sprzedaży, a odchylenie standardowe wyniku finansowego zależy od odchylenia standardowego wielkości sprzedaży.
Prawdopodobieństwo osiągnięcia BEP
Kolejnym krokiem jest wyznaczenie prawdopodobieństwa osiągnięcia obliczonego progu rentowności, w tym celu trzeba najpierw dokonać standaryzacji wyniku finansowego, dokonać tego można korzystając ze wzoru:
Zo - rozpatrywany poziom wyniku finansowego
To - zestandaryzowana wartość wyniku finansowego
Wartość ta wskazuje ile odchyleń standardowych wyniku finansowego stanowi różnica między założonym poziomem zysku ZO a jego wartością średnią mZ.
Wynik finansowy dla progu rentowności wynosi zero, a więc wartość zestandaryzowana tego wyniku będzie wynosiła:
Na podstawie dotychczasowych obliczeń, a konkretnie założonego poziomu wyniku finansowego i jego wartości zestandaryzowanej, można wyznaczyć dwa rodzaje prawdopodobieństwa:
- prawdopodobieństwa osiągnięcia wyniku finansowego mniejszego bądź równego względem ustalonego poziomu Z0, jako wartość dystrybuanty rozkładu normalnego w punkcie T0.
P (Z<=Zo)=F (To)
- prawdopodobieństwo osiągnięcia wyniku finansowego większego niż założony poziom Z0, jako dopełnienie poprzedniego wzoru do jedności.
P (Z>Zo)=1-F (To)
Analiza ta dostarcza informacji, co do realności osiągnięcia obliczonego progu rentowności.
| Próg rentowności — artykuły polecane |
| Margines bezpieczeństwa — Kalkulacja cen na podstawie kosztu jednostkowego — NPV — Dochodowe metody wyceny przedsiębiorstw — Wskaźnik rentowności — Średni ważony koszt kapitału — Zysk operacyjny — Błąd względny — Analiza Du Ponta |
Bibliografia
- Nowak E. (2008), Analiza sprawozdań finansowych, Polskie Wydawnictwo Ekonomiczne, Warszawa
- Nowak E. (2009), Zaawansowana rachunkowość zarządcza, Polskie Wydawnictwo Ekonomiczne, Warszawa
- Sierpińska M., Jachna T. (2006), Ocena przedsiębiorstwa według standardów światowych, PWN, Warszawa
- Sobańska I. (2010), Rachunkowość zarządcza. Podejście operacyjne i strategiczne, Wydawnictwo C.H. Beck, Warszawa
- Sojak S. (2012), Analiza progu rentowności, Rachunkowość, nr 10
- Żwirbla A. (2014), Nowa metoda analizy progu rentowności oraz dźwigni ekonomicznych, Zeszyty Naukowe WSHE, Tom XXXIX, s. 87
Autor: Piotr Byrski, Karolina Kruszczak