Wykres słupkowy: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m (cleanup bibliografii i rotten links) |
||
| (Nie pokazano 7 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
'''Wykres słupkowy''' jest jednym z najpopularniejszych typów wykresów stosowanych w analizie danych. Jest to graficzne przedstawienie danych statystycznych, w którym wartości są reprezentowane przez pionowe słupki. Każdy słupek reprezentuje osobne kategorie lub grupy danych, a wysokość słupka odzwierciedla [[wartość]] tej kategorii. | '''Wykres słupkowy''' jest jednym z najpopularniejszych typów wykresów stosowanych w analizie danych. Jest to graficzne przedstawienie danych statystycznych, w którym wartości są reprezentowane przez pionowe słupki. Każdy słupek reprezentuje osobne kategorie lub grupy danych, a wysokość słupka odzwierciedla [[wartość]] tej kategorii. | ||
| Linia 19: | Linia 4: | ||
==Układ wykresu== | ==Układ wykresu== | ||
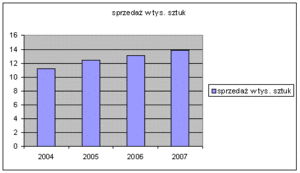
Wykresy słupkowe mają postać prostokątów (słupków) równoległych do siebie. Każdy z prostokątów przedstawia liczebność danego wariantu cechy. Im liczniej reprezentowany jest dany [[wariant]] cechy w zbiorowości, tym wyższy będzie słupek odpowiadający temu wariantowi. | Wykresy słupkowe mają postać prostokątów (słupków) równoległych do siebie. Każdy z prostokątów przedstawia liczebność danego wariantu cechy. Im liczniej reprezentowany jest dany [[wariant]] cechy w zbiorowości, tym wyższy będzie słupek odpowiadający temu wariantowi. | ||
| Linia 29: | Linia 13: | ||
* W arkuszu kalkulacyjnym Ms Excel wykres słupkowy traktowany jest jako 2 odrębne kategorie: wykres słupkowy (słupki poziome) i kolumnowy (słupki pionowe). Co więcej arkusz ten pozwala stworzyć wykres słupkowy, gdzie zamiast prostokątów występują prostopadłościany. | * W arkuszu kalkulacyjnym Ms Excel wykres słupkowy traktowany jest jako 2 odrębne kategorie: wykres słupkowy (słupki poziome) i kolumnowy (słupki pionowe). Co więcej arkusz ten pozwala stworzyć wykres słupkowy, gdzie zamiast prostokątów występują prostopadłościany. | ||
* Zgodnie z teorią statystyki słupki muszą być dwuwymiarowe (być prostokątami), ich układ z kolei (poziomy lub pionowy) jest dowolny. Wykres, w którym słupki są trójwymiarowe określa się mianem wykresu bryłowego <ref>(A. Bielecka 2001,"Statystyka w zarządzaniu - opis statystyczny" s. 54)</ref> | * Zgodnie z teorią statystyki słupki muszą być dwuwymiarowe (być prostokątami), ich układ z kolei (poziomy lub pionowy) jest dowolny. Wykres, w którym słupki są trójwymiarowe określa się mianem wykresu bryłowego <ref>(A. Bielecka 2001,"Statystyka w zarządzaniu - opis statystyczny" s. 54)</ref> | ||
<google>n</google> | |||
==Konstrukcja wykresu słupkowego== | ==Konstrukcja wykresu słupkowego== | ||
===Wykorzystanie skali arytmetycznej=== | ===Wykorzystanie skali arytmetycznej=== | ||
[[Plik:Wykres słupkowy 2.gif|right|300px|thumb|'''Rys. 2. Wykres słupkowy''']] | |||
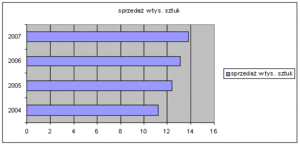
Wykres słupkowy korzysta z osi pionowej, która reprezentuje wartości danych. Ta oś jest zazwyczaj skalowana w sposób arytmetyczny, co oznacza, że odległość między kolejnymi wartościami jest stała. [[Skala]] ta umożliwia porównywanie względnych różnic między wartościami w sposób intuicyjny. | Wykres słupkowy korzysta z osi pionowej, która reprezentuje wartości danych. Ta oś jest zazwyczaj skalowana w sposób arytmetyczny, co oznacza, że odległość między kolejnymi wartościami jest stała. [[Skala]] ta umożliwia porównywanie względnych różnic między wartościami w sposób intuicyjny. | ||
| Linia 75: | Linia 62: | ||
Przykładem zastosowania uporządkowania danych na wykresie słupkowym może być przedstawienie [[ranking]]u popularności różnych produktów w danym sezonie sprzedażowym. Wykorzystując wykres słupkowy, można przedstawić produkty w kolejności malejącej popularności, umożliwiając łatwe porównanie i identyfikację najbardziej i najmniej popularnych produktów. | Przykładem zastosowania uporządkowania danych na wykresie słupkowym może być przedstawienie [[ranking]]u popularności różnych produktów w danym sezonie sprzedażowym. Wykorzystując wykres słupkowy, można przedstawić produkty w kolejności malejącej popularności, umożliwiając łatwe porównanie i identyfikację najbardziej i najmniej popularnych produktów. | ||
{{infobox5|list1={{i5link|a=[[Histogram]]}} — {{i5link|a=[[Średnia]]}} — {{i5link|a=[[Skala porządkowa]]}} — {{i5link|a=[[Dominanta]]}} — {{i5link|a=[[Skala interwałowa]]}} — {{i5link|a=[[Wykres kołowy]]}} — {{i5link|a=[[Wykres pudełkowy]]}} — {{i5link|a=[[Analiza regresji]]}} — {{i5link|a=[[Metody statystyczne]]}} }} | |||
==Przypisy== | ==Przypisy== | ||
| Linia 83: | Linia 72: | ||
* Aczel A. (2018), ''Statystyka w zarządzaniu'', Wydawnictwo Naukowe PWN, Warszawa | * Aczel A. (2018), ''Statystyka w zarządzaniu'', Wydawnictwo Naukowe PWN, Warszawa | ||
* Bielecka A. (2001), ''Statystyka w zarządzaniu - opis statystyczny'', Wydawnictwo WSPiZ im. L. Koźmińskiego, Warszawa | * Bielecka A. (2001), ''Statystyka w zarządzaniu - opis statystyczny'', Wydawnictwo WSPiZ im. L. Koźmińskiego, Warszawa | ||
* Dusza D. | * Dusza D. (2010), ''Podstawy statystyki dla studentów administracji'', Wydawnictwo Wyższa Szkoła Administracji w Bielsku Białej | ||
* Maksimowicz-Ajchel A. | * Maksimowicz-Ajchel A. (2007), ''Wstęp do statystyki. Metody opisu statystycznego'', Wydawnictwo Uniwersytetu Warszawskiego, Warszawa | ||
* Paradysz J. | * Paradysz J. (2005), ''Statystyka'', Akademia Ekonomiczna w Poznaniu, Poznań | ||
* Roeske-Słomka I. (2010), ''Statystyka opisowa'', Wydawnictwo Uniwersytetu Ekonomicznego w Poznaniu, Poznań | * Roeske-Słomka I. (2010), ''Statystyka opisowa'', Wydawnictwo Uniwersytetu Ekonomicznego w Poznaniu, Poznań | ||
* Starzyńska W. (2004), ''Podstawy statystyki'', Difin, Warszawa | * Starzyńska W. (2004), ''Podstawy statystyki'', Difin, Warszawa | ||
Aktualna wersja na dzień 20:49, 17 gru 2023
Wykres słupkowy jest jednym z najpopularniejszych typów wykresów stosowanych w analizie danych. Jest to graficzne przedstawienie danych statystycznych, w którym wartości są reprezentowane przez pionowe słupki. Każdy słupek reprezentuje osobne kategorie lub grupy danych, a wysokość słupka odzwierciedla wartość tej kategorii.
Wykres słupkowy jest szczególnie przydatny do porównywania wartości między różnymi kategoriami lub grupami. Może być stosowany zarówno do danych ilościowych, jak i jakościowych. Jego prostota i czytelność sprawiają, że jest powszechnie stosowany w różnych dziedzinach, takich jak ekonomia, marketing, nauki społeczne i wiele innych.
Układ wykresu
Wykresy słupkowe mają postać prostokątów (słupków) równoległych do siebie. Każdy z prostokątów przedstawia liczebność danego wariantu cechy. Im liczniej reprezentowany jest dany wariant cechy w zbiorowości, tym wyższy będzie słupek odpowiadający temu wariantowi.
Za pomocą prostokątów (słupków) w dwuwymiarowym układzie kartezjańskim pokazuje się ilościowe dane, które służą albo ukazaniu struktury danego zjawiska (np. odsetek osób głosujących na daną partię polityczną), albo zmiany danej cechy statystycznej w czasie (np. dynamika sprzedaży w określonych latach). Wykres słupkowy używamy przy prezentacji badanej zbiorowości zarówno ze względu na cechę ilościową (mierzalną), jak i jakościową (niemierzalną).
Historia i ciekawostki
- Pierwszy raz w historii, wykres słupkowy został użyty przez Williama Playfaira w 1786 roku w "The Commercial and Political Atlas". Ukazywał on wielkość importu oraz eksportu pomiędzy Szkocją a jej partnerami handlowymi.
- W arkuszu kalkulacyjnym Ms Excel wykres słupkowy traktowany jest jako 2 odrębne kategorie: wykres słupkowy (słupki poziome) i kolumnowy (słupki pionowe). Co więcej arkusz ten pozwala stworzyć wykres słupkowy, gdzie zamiast prostokątów występują prostopadłościany.
- Zgodnie z teorią statystyki słupki muszą być dwuwymiarowe (być prostokątami), ich układ z kolei (poziomy lub pionowy) jest dowolny. Wykres, w którym słupki są trójwymiarowe określa się mianem wykresu bryłowego [1]
Konstrukcja wykresu słupkowego
Wykorzystanie skali arytmetycznej
Wykres słupkowy korzysta z osi pionowej, która reprezentuje wartości danych. Ta oś jest zazwyczaj skalowana w sposób arytmetyczny, co oznacza, że odległość między kolejnymi wartościami jest stała. Skala ta umożliwia porównywanie względnych różnic między wartościami w sposób intuicyjny.
Wykorzystanie skali arytmetycznej pozwala również na dodanie wartości na osi pionowej, co ułatwia odczytanie konkretnych wartości reprezentowanych przez słupki. Jednak w niektórych przypadkach, gdy wartości są bardzo różne, może być konieczne zastosowanie logarytmicznej skali osi.
Elementy składowe wykresu słupkowego
Wykres słupkowy składa się z kilku istotnych elementów, które pomagają zrozumieć prezentowane dane. Pierwszym z nich jest tytuł, który powinien jasno określać temat wykresu. Tytuł powinien być zwięzły, ale jednocześnie dostarczać wystarczających informacji, aby czytelnik mógł zrozumieć, co prezentuje wykres.
Kolejnym ważnym elementem jest źródło danych, które powinno być podane na wykresie. Źródło to informacja o tym, skąd pochodzą prezentowane dane i może być pomocne w weryfikacji ich wiarygodności.
Dodatkowo, wykres słupkowy może zawierać legendę, która wyjaśnia, co reprezentuje każdy słupek na wykresie. Legendy są szczególnie przydatne, gdy wykres obejmuje wiele kategorii lub grup danych, które trzeba odróżnić.
Zależność od rodzaju szeregu statystycznego
Forma wykresu słupkowego może się różnić w zależności od rodzaju szeregu statystycznego i charakteru prawidłowości danych. W przypadku danych ilościowych, słupki mogą być przedstawione jako ciągłe pionowe linie, które reprezentują przedziały wartości. Natomiast dla danych jakościowych, słupki mogą być oddzielone od siebie i reprezentować konkretne kategorie.
Ponadto, wykres słupkowy może przyjmować różne formy, w zależności od charakteru prawidłowości danych. Na przykład, może to być wykres słupkowy prosty, w którym wysokość słupków odzwierciedla bezpośrednio wartości danych. Może to być również wykres słupkowy skumulowany, w którym słupki są nakładane na siebie, aby pokazać sumę wartości dla każdej kategorii.
Wykres słupkowy może również być używany do przedstawienia tendencji czasowych, co oznacza, że wartości są przedstawione w kolejności chronologicznej. W takim przypadku, osią poziomą wykresu może być czas, a słupki reprezentują wartości dla poszczególnych okresów.
Zastosowanie wykresu słupkowego
Porównywanie wartości między kategoriami
Wykres słupkowy jest jednym z najbardziej popularnych narzędzi w analizie danych, umożliwiającym porównywanie wartości między różnymi kategoriami. Dzięki temu rodzajowi wykresu możemy łatwo zobaczyć, jakie są różnice i podobieństwa między danymi, co jest niezwykle przydatne w procesie podejmowania decyzji.
Przykładem zastosowania wykresu słupkowego może być porównanie sprzedaży różnych produktów w określonym okresie czasu. Wykorzystując wykres słupkowy, możemy szybko zidentyfikować, który produkt cieszy się największym popytem, a który wymaga większego zaangażowania w celu zwiększenia sprzedaży.
Przedstawianie zmian w czasie
Innym zastosowaniem wykresu słupkowego jest przedstawianie zmian w czasie. Dzięki temu narzędziu możemy obserwować rozwój danego zjawiska lub wskaźnika w kolejnych okresach czasu. Dzięki porównaniu słupków dla różnych lat lub miesięcy, możemy łatwo zobaczyć, czy dana wartość wzrosła, spadła czy pozostała na podobnym poziomie.
Przykładem może być wykorzystanie wykresu słupkowego do przedstawienia zmian w przychodach firmy w ciągu ostatnich pięciu lat. Dzięki temu wykresowi można zobaczyć, czy firma osiągała sukcesywnie większe zyski, czy też miała okresy spadku. Jest to ważne w celu zidentyfikowania trendów i podejmowania odpowiednich działań.
Wykorzystanie różnych kształtów słupków na wykresie słupkowym
Wykres słupkowy umożliwia również wykorzystanie różnych kształtów słupków, co może dostarczyć dodatkowych informacji. Na przykład, można użyć słupków o różnych kolorach, aby oznaczyć różne kategorie lub grupy danych. Można również użyć słupków o różnej szerokości, aby wskazać różnice w wielkości wartości.
Wykorzystanie różnych kształtów słupków może również pomóc w wyróżnieniu szczególnie istotnych danych lub podkreśleniu pewnych trendów. Na przykład, można użyć słupków o większej wysokości lub grubości, aby wskazać na wartości odstające lub ważne punkty danych.
Prezentacja danych niestandardowych
Wykres słupkowy jest elastycznym narzędziem, które można dostosować do prezentacji danych niestandardowych. Można go użyć do przedstawienia różnych rodzajów informacji, takich jak odsetki, ilości, procenty, proporcje, wartości bezwzględne czy względne. Dzięki temu narzędziu można zobrazować wiele różnych typów danych w atrakcyjny i czytelny sposób.
Przykładem zastosowania wykresu słupkowego do prezentacji danych niestandardowych może być porównanie udziału rynkowego różnych firm w danym sektorze. Wykorzystując wykres słupkowy, można łatwo zobaczyć, jaką część rynku poszczególne firmy zajmują i jakie są między nimi różnice.
Uporządkowanie danych na wykresie słupkowym
Wykres słupkowy umożliwia łatwe uporządkowanie danych, co jest niezwykle przydatne w analizie i prezentacji informacji. Można uporządkować dane alfabetycznie, chronologicznie lub według wartości, co ułatwia porównywanie i interpretację danych.
Przykładem zastosowania uporządkowania danych na wykresie słupkowym może być przedstawienie rankingu popularności różnych produktów w danym sezonie sprzedażowym. Wykorzystując wykres słupkowy, można przedstawić produkty w kolejności malejącej popularności, umożliwiając łatwe porównanie i identyfikację najbardziej i najmniej popularnych produktów.
| Wykres słupkowy — artykuły polecane |
| Histogram — Średnia — Skala porządkowa — Dominanta — Skala interwałowa — Wykres kołowy — Wykres pudełkowy — Analiza regresji — Metody statystyczne |
Przypisy
- ↑ (A. Bielecka 2001,"Statystyka w zarządzaniu - opis statystyczny" s. 54)
Bibliografia
- Aczel A. (2018), Statystyka w zarządzaniu, Wydawnictwo Naukowe PWN, Warszawa
- Bielecka A. (2001), Statystyka w zarządzaniu - opis statystyczny, Wydawnictwo WSPiZ im. L. Koźmińskiego, Warszawa
- Dusza D. (2010), Podstawy statystyki dla studentów administracji, Wydawnictwo Wyższa Szkoła Administracji w Bielsku Białej
- Maksimowicz-Ajchel A. (2007), Wstęp do statystyki. Metody opisu statystycznego, Wydawnictwo Uniwersytetu Warszawskiego, Warszawa
- Paradysz J. (2005), Statystyka, Akademia Ekonomiczna w Poznaniu, Poznań
- Roeske-Słomka I. (2010), Statystyka opisowa, Wydawnictwo Uniwersytetu Ekonomicznego w Poznaniu, Poznań
- Starzyńska W. (2004), Podstawy statystyki, Difin, Warszawa
- Zeliaś A. (2001), Metody statystyczne, Polskie Wydawnictwo Ekonomiczne, Warszawa
- Ziuziański P. (2015), Kokpit menedżerski jako narzędzie do wizualizacji danych w kontekście zarządzania wiedzą w organizacji, Ekonomia i Zarządzanie, Oficyna Wydawnictwa Politechniki Białostockiej, nr 1
Autor: Łukasz Nowak, Michał Jurczak