Funkcja użyteczności

Funkcja użyteczności
Polecane artykuły
Krańcowa stopa substytucji Izokwanta Krzywa obojętności Elastyczność cenowa popytu Krzywa możliwości produkcyjnych Prawo Gossena Użyteczność krańcowa Linia budżetowa Produkt krańcowy

Funkcja użyteczności jest sposobem przyporządkowywania liczb każdemu koszykowi konsumpcji, w taki sposób iż bardziej preferowane koszyki otrzymują wyższe numery. Oznacza to, że koszyk A jest preferowany bardziej niż koszyk B wtedy i tylko wtedy gdy koszyk A ma większą użyteczność od koszyka B.

Gdy zwracamy uwagę tylko na określenie kolejności i hierarchii owych koszyków to taki rodzaj użyteczności w literaturze określany jest mianem użyteczności porządkowej (ordynalnej), gdyż kładzie on nacisk na porządkowanie konsumowanych koszyków dóbr. Geometrycznym obrazem takich funkcji użyteczności są np. krzywe obojętności. Koszyki leżące na tej samej krzywej obojętności muszą mieć tę samą użyteczność.

W opracowaniach spotyka się również pojęcie użyteczności kardynalnej, która w przeciwieństwie do użyteczności porządkowej określałaby różnicę w preferowaniu jednego koszyka względem drugiego. Jednakże problem w wyborze odpowiedniego miernika i brak potrzeby dokładnego określania owej różnicy, przesądza o tym, iż ta teoria nie jest obiektem większego zainteresowania przy opisie procesu dokonywania wyboru.

Funkcja jest rosnąca ponieważ każdy dąży do posiadania większej ilości niż mniejszej. Dodatkowo przy każdym kolejnym powiększeniu się dobra lub bogactwa wzrost funkcji użyteczności jest mniejszy (użyteczność krańcowa jest malejąca).

Użyteczność to całokształt zadowolenie z posiadania jakiejś rzeczy lub dobra, czy jego konsumpcji przez odbiorcę, poniekąd jest to kategoria abstrakcyjna.

TL;DR

Funkcja użyteczności jest sposobem przyporządkowywania liczb koszykom konsumpcji, aby określić ich preferencje. Istnieją różne rodzaje funkcji użyteczności, takie jak porządkowa czy kardynalna. Funkcje użyteczności mogą być rysowane na wykresach lub opisywane za pomocą wzorów. Istnieją różne przykłady funkcji użyteczności, takie jak substytuty doskonałe, dobra doskonale komplementarne, preferencje quasi-liniowe i preferencje typu Cobba-Douglasa. Użyteczność marginalna odzwierciedla zadowolenie z jednostkowej zmiany konsumpcji, a skłonność do ryzyka wpływa na kształt funkcji użyteczności.

Budowanie funkcji użyteczności

Rys. 1 Funkcja użyteczności - krzywe obojętności

Na samym początku trzeba odpowiedzieć sobie na pytanie, czy zawsze możemy zbudować funkcję użyteczności (porządkowej). Odpowiedź brzmi, iż nie zawsze. Spowodowane jest to możliwością wystąpienia nieprzechodniości preferencji np. gdy koszyk A>B>C>A, co oznaczałby po przyporządkowaniu liczb, że u (A)> u (B)> u (C)> u (A), a taka sytuacja jest niemożliwa i w konsekwencji napotykamy na trudności w zbudowaniu funkcji użyteczności. Gdy jednak odrzucimy wyjątek dotyczący nieprzechodniości to w większości przypadków możemy skonstruować funkcję użyteczności.

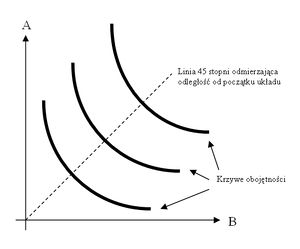
Graficzne przedstawienie funkcji użyteczności sprowadza się do poprowadzenia w układzie współrzędnych półprostej pod kątem 45 stopni i oznaczenia każdej krzywej obojętności zależnie od tego w jakiej odległości znajduje się ona od początku układu współrzędnych, mierzonej wzdłuż tej linii. Krzywe obojętności mają nachylenie ujemne i są wypukłe względem początku układu współrzędnych, co wydaje się logiczne z tego względu, iż dodatnie nachylenie oznaczało by większą ilość obu dóbr i w konsekwencji wyższą użyteczność. Dokładny kształt krzywej określa marginalna stopa substytucji (patrz również użyteczność krańcowa).

Funkcje użyteczności możemy rysować znając wzór opisujący preferencje konsumenta. W drugą stronę, wyznaczenie zależności funkcyjnej z graficznego obrazu funkcji jest nieco trudniejsze i bardziej intuicyjne.

Niektóre przykłady funkcji użyteczności

Rys. 2 Krzywe obojętności dla dóbr A i B będących doskonałymi substytutami

Substytuty doskonałe

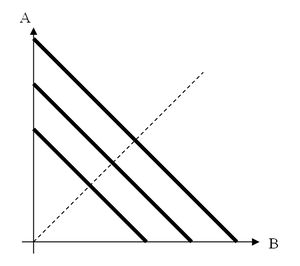
W przypadku koszyków, które cechują się doskonałą substytucyjnością znaczenie ma jedynie suma dóbr. Dlatego w tym przypadku możemy zastosować zależność funkcyjną u (A, B) = A + B bądź inną jej monotoniczną transformację. Chyba, że dane dobra konsument nie jest skłonny wymieniać w stosunku 1:1. Wtedy posługujemy się odpowiednimi parametrami np. u (A, B) = aA + bB (gdzie a i b są dodatnie).

Dobra doskonale komplementarne

Rys. 3 Krzywe obojętności dla dóbr A i B cechujących się doskonałą komplementarnością

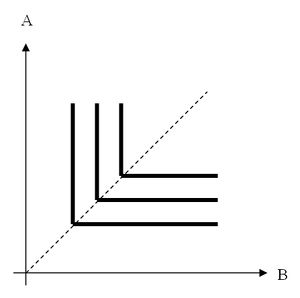
Dobra doskonale komplementarne to takie, których użyteczność jest teoretycznie żadna w przypadku ich osobnej konsumpcji. Najlepszym przykładem jest tu lewy i prawy but, posiadanie tylko lewego lub tylko prawego buta jest dla konsumenta racjonalnie bezużyteczne. Funkcja użyteczności w tym przypadku wygląda następująco u (A, B) = min {A, B}. A ogólniej, gdy mamy do czynienia z konsumowaniem dóbr w innej proporcji niż 1:1, to funkcja użyteczności przybiera postać u (A, B) = min {aA, bB}.

Preferencje quasi-liniowe

Rys. 4 Graficzna ilustracja zależności quasi-liniowej dla dóbr A i B

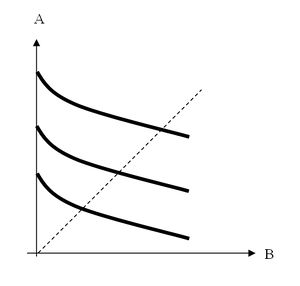
W tym przypadku k.o. są przesunięte wzajemnie pionowo w dół. Równanie funkcji przyjmuje postać B = k - v (A), gdzie k jest różną stałą na rożnych krzywych obojętności. W tym przypadku w dziedzina dobra B funkcji użyteczności jest liniowa, a w przypadku dobra A jest nieliniowa (stąd nazwa quasi-liniowa czyli częściowo liniowa), co wynika z rozwiązania równania względem stałej k. Szczególnym przypadkiem funkcji quasi-liniowej może być: u (A, B) = pier.A + B lub u (A, B) = lnA + B. Funkcje quasi-liniowe są mało realistyczne, ale wygodnie można się nimi posługiwać.

Preferencje typu Cobba-Douglasa

Funkcja użyteczności Cobba-Douglasa ma postać: u (A, B) = A^c*B^d gdzie c, d są dodatnimi liczbami. Funkcje tej postaci są bardzo użyteczne w prezentowaniu wielu algebraicznych problemów ekonomicznych. Przykładem jest zastosowanie tego typu preferencji przy funkcji produkcji, sformułowanej przez Knuta Wicksella, która przedstawia się następująco F (K, L) = aK^alpha L^beta, K, L większe równe 0.

Użyteczność marginalna

Przedstawia zadowolenie użytkownika ze zmniejszenia lub zwiększenia o jedną jednostkę konsumpcji jakiegoś dobra. Ta użyteczność maleje, gdy ilość konsumowanego dobra rośnie. Zadowolenie konsumenta za pierwszym razem, gdy dostanie dane dobro jest zdecydowanie większe niż podczas konsumowania kolejnego. Może się zdarzyć, że użyteczność marginalna będzie ujemna, gdy odbiorca przekroczy jakąś ilość wielkości konsumpcji i pozyskiwanie tego dobra będzie wiązało się z niezadowoleniem.

Użyteczność, a skłonność do ryzyka

Czym bardziej konsument jest skłonny do ryzyka, tym funkcja użyteczności jest bardziej wypukła. Tym samym funkcja użyteczności jest bardziej wklęsła, jeżeli decydent jest mniej gotowy na ryzyka. W wielu dziedzinach życia określenie właściwego poziomu ryzyka byłoby dużym ułatwieniem, ale zawsze będzie to decyzja w jakiś sposób subiektywna dla podmiotu. Niejednokrotnie przedstawienie tego poziomu dla określonej sytuacji przez dwa różne podmioty może się znacząco różnić. Dlatego też, nie da się przedstawić odpowiedniego poziomu ryzyka, ponieważ jest to kwestia indywidualnego podejścia.

Bibliografia

• Begg D. (2007). Mikroekonomia, Wydawnictwo Naukowe PWE, Warszawa
• Klimczak B. (2003). Mikroekonomia, Wydawnictwo Akademii ekonomicznej im. Oskara Langego, Wrocław
• Rekowski M. (2002). Wprowadzenie do mikroekonomii, WROKOPA, Poznań
• Tyszka T. (2004). Czy istnieje ogólna skłonność jednostki do ryzyka?, "Decyzje", nr 2
• Varian H. (2002). Mikroekonomia. Kurs średni - ujęcie nowoczesne, Wydawnictwo Naukowe PWN, Warszawa

Autor: Piotr Gawlewicz, Anna Liszka