Korelacja

Korelacja jako termin statystyczny jest to poziom relacji liniowej (relacja która zwiększa się lub zmniejsza w stałym tempie) pomiędzy zmiennymi liczbowymi [Deborah J. Rumsey 2016, s. 79]

Przyjmijmy, że zmienna niezależna (objaśniająca) X oraz zmienna zależna (objaśniana) Y są zmiennymi losowymi. Korelacja między dwiema losowymi zmiennymi X i Y jest miarą siły (stopnia) liniowego związku między tymi zmiennymi.

Korelacja jako statystyka stwierdza istnienie zależności między dwiema zmiennymi X i Y jednak nie jest w stanie wyjaśnić dlaczego występują i w jaki sposób powstały. Analiza korelacji jest ściśle powiązana z analizą liniowej regresji dwóch zmiennych z czego analiza regresji dochodzi do opisu związku za pomocą funkcji regresji. Natomiast analiza korelacji określa nam miarę intensywności (siły) zależności liniowej. Pojęcie korelacji w praktyce przybiera szersze znaczenie, obejmując również zależności nieliniowe. W statystyce miara stosowana przy zależnościach nieliniowych to wskaźnik lub stosunek korelacyjny. [J. Podgórski 2010, s. 334]

W analizie korelacji jednakowo traktuje się obie zmienne: zależną i niezależną. Analiza ta pokazuje, na ile obie zmienne zmieniają się równocześnie w sposób liniowy. Korelacja między X i Y jest taka sama jak między Y i X.

TL;DR

Korelacja to miara siły związku liniowego między zmiennymi. Analiza korelacji pokazuje, jak obie zmienne zmieniają się równocześnie. Współczynnik korelacji mieści się w przedziale od - 1 do +1. Korzystając z diagramów korelacyjnych, można ocenić siłę i kierunek zależności między zmiennymi. Tablice korelacyjne ułatwiają analizę związku korelacyjnego. Współczynnik korelacji interpretuje się jako siłę zależności między zmiennymi.

Właściwości korelacji

Do istotnych właściwości współczynnika korelacji należą:

• Korelacja zawsze mieści się w przedziale od - 1 do +1
• Korelacja to miara niemianowana. Jeśli zmienimy jednostki dla X lub Y, wartość korelacji nie ulegnie zmianie. Przykładowo zmiana jednostek temperatury ze stopni Fahrenheita na stopnie Celsjusza nie wpłynie na korelację z daną zmienną.
• W danym zbiorze można zamieniać zmienne X i Y bez zmiany korelacji

Diagramy korelacyjne

Rys. 1. Korelacyjne wykresy rozrzutu; 1 - korelacja liniowa dodatnia, 2 - korelacja liniowa ujemna, 3 - brak korelacji, 4 - korelacja krzywoliniowa

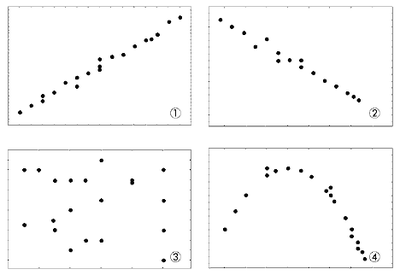
Często wykorzystywanym w praktyce sposobem stwierdzania, czy istnienie korelacja między dwiema zmiennymi, jest diagram punktowy, zwany też diagramem korelacyjnym. Diagram korelacyjny w prostokątnym układzie współrzędnych, tworzy się odkładając na osiach wartości badanych zmiennych (por. rys. 1). Każda z obserwacji ma dwie współrzędne. Pierwsza z nich odnosi się do pierwszego elementu danych w parze (jest to współrzędna X, czyli wartość o jaką przemieszczamy się w lewo lub w prawo). Druga współrzędna odpowiada drugiemu elementowi danych w parze (jest to współrzędna Y, czyli wartość o jaką przemieszczamy się w górę lub w dół). Punkt oznaczający daną obserwację umieszczamy w miejscu przecięcia się dwóch współrzędnych. Na osi odciętych zaznaczamy wartości tej zmiennej, którą przyjmujemy za niezależną (objaśniającą), wyrażającą ilościowo zjawisko traktowane jako przyczyna, natomiast na osi rzędnych wartości tej zmiennej, którą przyjmujemy za zależną (objaśnianą), wyrażającą ilościowo zjawisko uznawane za skutek. Punkty umieszczone w takim układzie współrzędnych tworzą mniej lub bardziej wyraźną "smugę", co daje możliwość wstępnej oceny siły i kierunku zależności oraz może być podstawą wyboru określonej funkcji matematycznej opisującej zależność między badanymi zmiennymi.

Interpretację wykresu rozrzutu uzyskujemy przemieszczając się od lewej do prawej w poszukiwaniu trendów w danych. Przykładowo, jeśli zauważamy, że dane wykazują układ rosnący możemy stwierdzić, że zależność pomiędzy X i Y jest pozytywna. W momencie gdy wartości dla X rosną (przemieszczają się w prawo), rosną także wartości dla Y (przemieszczają się w górę). Natomiast jeśli analizując wykres od lewej do prawej strony, zauważamy, że dane układają się w sposób malejący, wskazuje to na negatywną zależność pomiędzy X i Y. Wraz ze wzrostem wartości X (przemieszczają się w prawą stronę) następuje spadek wartości Y (przemieszczają się w dół). W przypadku gdy dane umieszczone na wykresie nie układają się w żaden uporządkowany wzór (nawet niejasny) nie istnieje żadna zależność między X i Y. [Deborah J. Rumsey 2016, s. 288]

Tablice korelacyjne

Tablica 1.

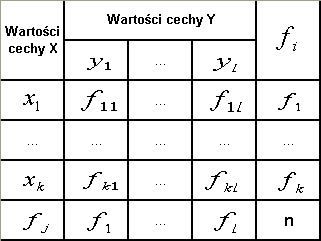
Gdy obserwacje statystyczne dotyczące badanych zmiennych są liczne, operowanie wartościami szczegółowymi jest uciążliwe. W celu stwierdzenia istnienia lub braku związku korelacyjnego konstruujemy wówczas tablicę korelacyjną. Na skrzyżowaniu kolumn z wierszami wpisywane są liczebności jednostek zbiorowości statystycznej, u których zaobserwowano jednoczesne występowanie określonej wartości xi i yj. Schemat tablicy korelacyjnej przedstawia Tablica 1.

Jak wynika z tablicy 1, zmienna losowa X przyjmuje k wariantów (i=1,2,..., k), zmienna losowa Y zaś l wariantów (j=1,2,..., l). Symbol $f_{j}$ oznacza liczbę jednostek, które maja wariant yj zmiennej Y, natomiast symbol $f_{i}$ - liczbę jednostek, które mają wariant xi zmiennej X. Symbole $f_{ij}$ oznacza liczbę jednostek, które posiadają jednocześnie wariant $x_{i}$ cechy X i wariant $y_{j}$ cechy Y. Symbol n oznacza liczebność próby.

O badaniu związku korelacyjnego można mówić tylko wtedy, gdy przynajmniej jedna zmienna jest mierzalna. W celu określenia stopnia zależności między badanymi zmiennymi można posłużyć się współczynnikiem korelacji. Współczynnik korelacji jest miernikiem siły zależności między badanymi zmiennymi.

Współczynnik korelacji w populacji, oznaczamy przez ρ, przyjmuje wartości z przedziału od - 1 do +1. Współczynnik korelacji w populacji: $\rho ={\frac {cov(X,Y)}{\sigma x\sigma y}}$

Możliwe wartości współczynnika interpretujemy następująco:

1. Gdy ρ = 0, to nie ma korelacji, czyli nie ma liniowego związku między dwiema zmiennymi losowymi.
2. Gdy ρ = 1, to zachodzi ścisły dodatni związek między dwiema zmiennymi. W tym przypadku, gdy wartości jednej ze zmiennych rosną, to i wartości drugiej rosną, a gdy wartości jednej spadają, to i wartości drugiej zmiennej spadają.
3. Gdy ρ = -1, to zachodzi ścisły ujemny związek między dwiema zmiennymi. Gdy jedna z tych zmiennych przyjmie większe wartości, to druga przyjmuje mniejsze wartości, a gdy wartości jednaj zmiennej spadają, to wartości drugiej zmiennej rosną.
4. Jeżeli bezwzględna wartość ρ mieści się wewnątrz przedziału [0,1], to mierzy ona siłę liniowego związku między dwiema zmiennymi.

Na przykład - wartość współczynnika korelacji 0,90 oznacza silny dodatni liniowy związek między zmiennymi. Wartość -0,70 współczynnika korelacji oznacza nieco słabszy i ujemny związek liniowy. Wartość współczynnika korelacji 0,30 oznacza słaby dodatni związek liniowy między zmiennymi.

Korelacja — artykuły polecane

Współczynnik korelacji rang Spearmana — Analiza regresji — Średnia — Wariancja składnika resztowego — Rozkład normalny — Kwartyl — Ciąg Fibonacciego — Dominanta — Rozkład częstości

Bibliografia

• Aczel A. (2018), Statystyka w zarządzaniu, Wydawnictwo Naukowe PWN, Warszawa
• Buszkowska E., (2015), Zastosowanie statystyki wielowymiarowej do badania kryzysu subprime, "Optimum. Studia Ekonomiczne", nr 4
• Podgórski J. (2010), Statystyka dla studiów licencjackich, Polskie Wydawnictwo Ekonomiczne, Warszawa
• Podgórski J. (2010), Statystyka dla studiów licencjackich, Polskie Wydawnictwo Ekonomiczne, Warszawa
• Rumsey D. (2016), Statystyka dla bystrzaków, Helion, Gliwice
• Słomczyński M., Sidor D., Rybicki T. (2012), Zapobieganie niepowodzeniom edukacyjnym w e-nauczaniu: wykorzystanie narzędzia Spector, EduAkcja. Magazyn edukacji elektronicznej, nr 2
• Sobczyk M. (2007), Statystyka, Wydawnictwo Naukowe PWN, Warszawa
• Sołtys J., Dorocki S. (2016), Wskaźniki przedsiębiorczości w jednostkach terytorialnych Polski-zróżnicowanie w czasie i przestrzeni, Przedsiębiorczość-Edukacja nr 12
• Starzyńska W. (2006), Statystyka praktyczna, Wydawnictwo Naukowe PWN, Warszawa

Autor: Anna Rycerska, Magdalena Postawa