Amplituda

Amplituda to najwyższy lub najniższy punkt w ruchu falowym lub drgającym. Inaczej mówiąc jest to różnica między wartościami maksymalnymi i minimalnymi osiąganymi podczas regularnej oscylacji. Jeśli f (t) przez pewien czas osiąga maksymalną wartość a i minimalną wartość b (D. Wakman, L. Weinstein 1997, s. 659). Amplituda oscylacji wynosi (a - b). Amplituda jest maksymalną wartością przesunięcia lub zmiany zmiennej ze średniej wartości podczas ruchu oscylacyjnego lub falowego. Nieujemna ilość skalarna, której wymiar pokrywa się z wymiarem określonej wielkości fizycznej (K. Knopp, B. Frederick 1996, s. 3).

TL;DR

Amplituda to różnica między wartościami maksymalnymi i minimalnymi w ruchu falowym lub drgającym. Istnieją różne rodzaje amplitudy, takie jak amplituda peak-to-peak, peak amplitude, poł-amplituda i średnia kwadratowa amplitudy. Amplituda może być używana do określania zmienności cen papierów wartościowych, ryzyka inwestycyjnego oraz zmian stóp inflacji. Może również odzwierciedlać zmiany w przychodach, kosztach i wydajności w przedsiębiorstwach.

Definicje

• Amplituda peak-to-peak - jest zmianą pomiędzy wartością maksymalną (najwyższa wartość amplitudy) i minimalną (najniższa wartość amplitudy, która może być ujemna)
• Peak amplitude - jeśli wartość zadana wynosi zero, jest to maksymalna wartość bezwzględna sygnału; jeśli referencja jest wartością średnią, jest to maksymalną wartością bezwzględną różnicy od tej wartości odniesienia
• Poł-amplituda - oznacza 1/2 (połowę) amplitudy od Peak-to-peak (Physics - Celestial Mechanics).
• Średnia kwadratowa amplitudy (Root mean square amplitude) - (RMS) stosowana jest w szczególności w elektrotechnice: RMS definiuje się jako pierwiastek kwadratowy średniej z czasem kwadratu pionowej odległości wykresu od stanu spoczynkowego (Physics - Celestial Mechanics).

Rys. 1 Średnia kwadratowa anplitudy

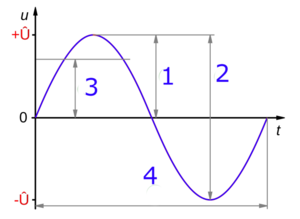
1) Peak amplitude (Maksymalna wartość)

2) Amplituda Peak-to-peak (Od najniższej do najwyższej wartości)

3) Średnia kwadratowa amplitudy

4) Okres

• Amplituda na przykładzie wzrostu ceny papieru wartościowego - amplituda to różnica w cenie papieru wartościowego od czasu jego cyklu fali (na dole) do szczytu lub maksimum jego ruchu cenowego w pewnym okresie czasu. Amplituda jest dodatnia, gdy obliczana jest korekta zwyżkowa (przy obliczaniu od dołu do szczytu) i ujemna podczas obliczania korekty od szczytu do dołu.
• Amplituda Breaking Down - amplituda pozwala na oszacowanie zmienności określonego zabezpieczenia. Im większa amplituda, albo dodatnia, albo ujemna, tym bardziej niestabilna jest ocena bezpieczeństwa. Poziom zmienności może również oznaczać poziom ryzyka występującego w danej inwestycji.

Rys. 2 Przykład amplitudy w ekonomii

• Peak or Trough - "Peak" jest identyfikowany jako najwyższy punkt cenowy, określony poziom zabezpieczenia osiągnięty w określonym czasie. Przy takim rozumieniu "peak" może się różnić w zależności od badanego okresu. ‘'Trough’' jest odwrotnością "Peak". Stanowi punkt, w którym zabezpieczenie miało najniższą cenę w tym samym okresie. W przypadku powiązania z produktem krajowym brutto (PKB) danego kraju, najniższy punkt w czasie kryzysu gospodarczego bezpośrednio poprzedzającego zwrot w kierunku poprawy sytuacji gospodarczej.

Rys. 3 Przykład amplitudy w przedsiębiorstwie

Określanie amplitudy w odniesieniu do Peaks and Troughs: Amplituda przedstawia różnicę pomiędzy punktem środkowym najwyższego punktu (Peak) a punktem środkowym najniższego punktu (trough) w danym okresie czasu. Każdy punkt środkowy określa się, znajdując różnicę między ekstremalnymi, takimi jak wyżej wymienione “peak and trough", a linią środkową. Linia środkowa może znajdować się w punkcie zero w przypadkach, w których możliwa jest zarówno wartość dodatnia, jak i ujemna. W innych przypadkach linia średnia może reprezentować średnią cenę papieru wartościowego w przypadkach, gdy wartości ujemne są niedozwolone. Amplitudę oblicza się odejmując jeden punkt środkowy od drugiego.

Przykłady

Rys. 4 Poziom pracy ludzi w przedsiębiorstwie

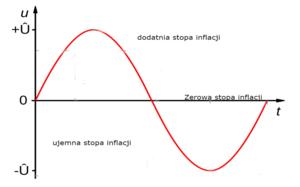
Przykład amplitudy w ekonomii W zakresie ekonomii, amplituda może pokazywać zmiany stopy inflacji danego kraju. Na przykład, ogólny trend wzrostu ceny dóbr i usług, czyli dodatnia stopa inflacji, jest to najwyższy punkt (Peak). Najniższy punkt (trough) - to ujemna stopa inflacji, kiedy cena dóbr i usług spada. Zerowa stopa inflacji to wartość środkowa, czyli 0.

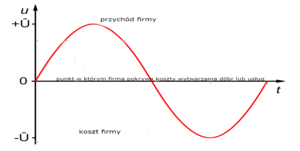
Przykład amplitudy w przedsiębiorstwie W przedsiębiorstwie amplituda może pokazywać przychody i koszty firmy. W takim razie najwyższy punkt wahań amplitudy odpowiada za przychód firmy. Z kolei największy koszt firmy - to najniższy punkt amplitudy. Wartość środkowa, czyli zero, to punkt, w którym firma pokrywa koszty wytwarzania dóbr lub usług.

Rys. 5 Poziom cen materiałów

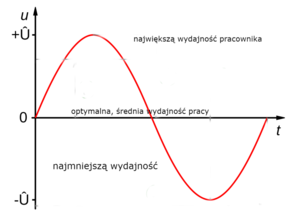
Amplituda może pokazywać poziom pracy ludzi w przedsiębiorstwie. Tutaj najwyższy punkt będzie odpowiadać za największą wydajność pracownika, a najniższy punkt - za najmniejszą wydajność. Wartość środkowa - to optymalna, średnia wydajność pracy przeciętnego pracownika.

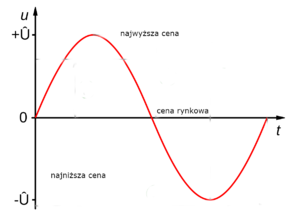
Amplituda może również pokazywać poziom cen materiałów dla wytwarzania dóbr i usług w jakimś przedsiębiorstwie. W tym przypadku najwyższy punkt wahań amplitudy - to najwyższa cena konkretnego materiału. Najniższy punkt wahań amplitudy - to najniższa cena proponowana przez wytwórcę. Wartość środkowa w tym przypadku będzie pokazywać cenę rynkową.

Amplituda — artykuły polecane

Elastyczność punktowa popytu — Utarg — Ceny stałe — Margines bezpieczeństwa — Deflator PNB — Realny kurs walutowy — Deflator PKB — Elastyczność podaży — Stopa inflacji — Infrastruktura informatyczna

Bibliografia

• Knopp K., Bagemihl F. (1996). Theory of Functions Parts I and II. “Dover Publications"
• Tatum J. B. (2007) Physics - Celestial Mechanics. Paragraph 18.2.12
• Wakman D., Weinstein L. (1997) Postęp w naukach fizycznych Tom 123

Autor: Volodymyr Perets