Punktowy diagram korelacji: Różnice pomiędzy wersjami
m (cleanup bibliografii i rotten links) |
mNie podano opisu zmian |
||
| Linia 19: | Linia 19: | ||
* "stwierdzenia istnienia zależności pomiędzy zmiennymi, | * "stwierdzenia istnienia zależności pomiędzy zmiennymi, | ||
* stwierdzenia kierunku związku, | * stwierdzenia kierunku związku, | ||
* pokazania siły związku."<ref> Soliński B., (2006). | * pokazania siły związku."<ref> Soliński B., (2006).</ref> | ||
==Tworzenie diagramu korelacji== | ==Tworzenie diagramu korelacji== | ||
| Linia 42: | Linia 42: | ||
==Współczynnik korelacji Pearsona== | ==Współczynnik korelacji Pearsona== | ||
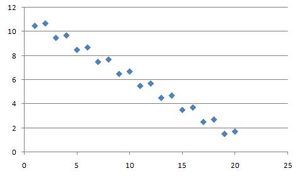
[[Plik:Korelacja ujemna.jpg|thumb|300px|Rys. 3. Ujemna]] | [[Plik:Korelacja ujemna.jpg|thumb|300px|Rys. 3. Ujemna]] | ||
Relację między dwoma zmiennymi (cechami) można również scharakteryzować przy pomocy współczynnika korelacji Pearsona (r<small>xy</small>), który służy do badania zależności liniowych. Jest on miarą siły związku liniowego pomiędzy zmiennymi mierzalnymi. Bezwzględna [[wartość]] współczynnika korelacji informuje o sile związku dwóch cech, natomiast jego znak - o kierunku zależności zachodzącej między dwoma zmiennymi. <ref>Krawczyk M. (red.) (2012). | Relację między dwoma zmiennymi (cechami) można również scharakteryzować przy pomocy współczynnika korelacji Pearsona (r<small>xy</small>), który służy do badania zależności liniowych. Jest on miarą siły związku liniowego pomiędzy zmiennymi mierzalnymi. Bezwzględna [[wartość]] współczynnika korelacji informuje o sile związku dwóch cech, natomiast jego znak - o kierunku zależności zachodzącej między dwoma zmiennymi. <ref>Krawczyk M. (red.) (2012)., s. 82-83</ref> Tabela poniżej przedstawia [[zakres]] współzależności zmiennych w zależności od wartości bezwzględnej r<small>xy</small>. | ||
{| class="wikitable" | {| class="wikitable" | ||
Wersja z 19:53, 28 paź 2023
| Punktowy diagram korelacji |
|---|
| Polecane artykuły |
Punktowy diagram korelacji to jedno z narzędzi, które stosowane są w procesie doskonalenia jakości. Jest to graficzna ilustracja związku zachodzącego między dwoma zmiennymi (cechami). Diagram taki stosujemy, gdy chcemy zbadać zależność pomiędzy dwoma czynnikami, np. zbadać ich zależność przyczynowo- skutkową.
Diagram korelacji służy do:
- "stwierdzenia istnienia zależności pomiędzy zmiennymi,
- stwierdzenia kierunku związku,
- pokazania siły związku."[1]
Tworzenie diagramu korelacji
Diagram korelacyjny otrzymujemy przez naniesienie w prostokątnym kładzie współrzędnych n punktów empirycznych odpowiadających obserwacjom dwóch zmiennych X i Y. Każdą z obserwacji opisujemy parą liczb: xi i yi odpowiadającą punktowi Pi (i = 1,2,..., n) w dwuwymiarowym układzie współrzędnych, gdzie na osi odciętych umieszczamy wartości zmiennej objaśniającej X, a na osi rzędnych - wartości zmiennej objaśnianej Y. W ten sposób otrzymujemy n punktów o współrzędnych (xi, yi). To, w jaki sposób grupowane są punkty na wykresie pokazuje zależności korelacyjne między badanymi zmiennymi. Najprostszy przypadek to liniowa korelacja między zmiennymi.
Typy Korelacji
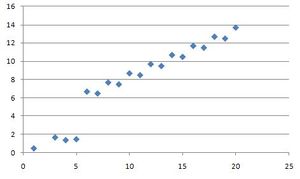
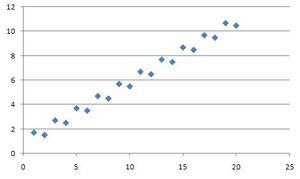
Korelacja dodatnia
Korelacja dodatnia - to przypadek, w którym wzrostowi (spadkowi) wartości jednej zmiennej towarzyszy wzrost (spadek) wartości drugiej zmiennej. Przykładem korelacji dodatniej może być związek między planowaną liczbą dni hospitalizacji pacjenta a szacunkowymi kosztami całkowitymi.
Korelacja ujemna
Korelacja ujemna - to przypadek, w którym wzrostowi (spadkowi) wartości jednej zmiennej towarzyszy spadek (wzrost) wartości drugiej zmiennej.
Brak korelacji
Brak korelacji - nie istnieje widoczna zależność pomiędzy wartościami.
Współczynnik korelacji Pearsona
Relację między dwoma zmiennymi (cechami) można również scharakteryzować przy pomocy współczynnika korelacji Pearsona (rxy), który służy do badania zależności liniowych. Jest on miarą siły związku liniowego pomiędzy zmiennymi mierzalnymi. Bezwzględna wartość współczynnika korelacji informuje o sile związku dwóch cech, natomiast jego znak - o kierunku zależności zachodzącej między dwoma zmiennymi. [2] Tabela poniżej przedstawia zakres współzależności zmiennych w zależności od wartości bezwzględnej rxy.
| Wartość bezwzględna z rxy | Zakres współzależności |
|---|---|
| rxy=0 | Współzależność nie występuje |
| 0< rxy<0,3 | Słaby stopień współzależności |
| 0,3≤ rxy<0,5 | Średni stopień współzależności |
| 0,5≤ rxy<0,7 | Znaczny stopień współzależności |
| 0,7≤ rxy<0,9 | Wysoki stopień współzależności |
| 0,9≤ rxy<1 | Bardzo wysoki stopień współzależności |
| rxy=1 | Współzależność całkowita (ścisłość) |
Źródło: Michalski T., (2008). Statystyka, WSiP, Warszawa, s. 152
Wskazówki dotyczące interpretacji punktowego diagramu korelacji
Rozrzut punktów na diagramie korelacji
Punktowy diagram korelacji przedstawia zależność między dwiema zmiennymi. Jednym z aspektów, które warto wziąć pod uwagę podczas interpretacji tego diagramu, jest rozrzut punktów na osiach. Szerokość i wysokość rozrzutu punktów mogą dostarczyć istotnych informacji na temat natury zależności między zmiennymi.
Duży rozrzut punktów na diagramie może sugerować brak lub słabą zależność między zmiennymi. W przypadku dużej szerokości i wysokości rozrzutu, można oczekiwać, że zmienne nie mają jednoznacznej zależności, a ich wartości są bardziej rozproszone. Może to wynikać z różnych czynników, takich jak duże zróżnicowanie próby, błąd pomiarowy, brak korelacji między zmiennymi lub obecność innych czynników zakłócających.
Z kolei mały rozrzut punktów wskazuje na silną zależność między zmiennymi. W przypadku małej szerokości i wysokości rozrzutu, można przypuszczać, że zmienne są silnie skorelowane i mają jednoznaczną zależność. Taki wynik może sugerować, że zmienne wpływają na siebie nawzajem i ich wartości są zbliżone.
Warto zwrócić uwagę na obecność wartości odstających na diagramie. Wartości odstające mogą wpływać na interpretację diagramu korelacji, ponieważ wywołują znaczące zmiany w statystykach dotyczących zależności między zmiennymi. W przypadku obecności wartości odstających, konieczne jest zbadanie przyczyn ich występowania i rozważenie ich wpływu na wyniki analizy korelacji.
Obecność wartości odstających
Wartości odstające to wartości, które znacząco odbiegają od reszty danych. Mogą mieć istotny wpływ na wyniki analizy korelacji i wymagają odpowiedniego rozpoznania i obsługi. W przypadku obecności wartości odstających na diagramie korelacji, interpretacja zależności między zmiennymi może być zakłócona.
Aby zidentyfikować wartości odstające, można skorzystać z różnych metod, takich jak analiza diagramu punktowego, testy statystyczne lub analiza skupień. Wartości odstające mogą być wynikiem błędów pomiarowych, nietypowych próbek lub rzadkich zdarzeń. Istnieje kilka sposobów obsługi wartości odstających, takich jak usunięcie ich z analizy, zastąpienie ich innymi wartościami lub zastosowanie technik obcinania.
Wartości odstające mogą wpływać na wyniki analizy korelacji, ponieważ mogą skrzywić rozkład danych i zmienić statystyki dotyczące zależności między zmiennymi. Dlatego ważne jest, aby dokładnie zbadać przyczyny występowania wartości odstających i ocenić ich wpływ na wyniki analizy.
Nieliniowe zależności
Punktowy diagram korelacji jest często wykorzystywany do badania zależności liniowych między zmiennymi. Jednakże, może nie być odpowiedni do badania nieliniowych zależności. W przypadku występowania nieliniowych zależności między zmiennymi, diagram korelacji może nie wykazywać jednoznacznej zależności, a rozrzut punktów może być niewłaściwie interpretowany.
W celu rozpoznania nieliniowych zależności na diagramie korelacji, można zastosować różne techniki, takie jak analiza wygładzania, transformacja danych lub zastosowanie innego typu diagramu, na przykład diagramu rozrzutu wielowymiarowego. Istnieją również inne narzędzia statystyczne, takie jak analiza regresji nieliniowej, które mogą być bardziej odpowiednie do badania nieliniowych zależności.
Warto zauważyć, że istnienie nieliniowej zależności między zmiennymi może mieć istotne konsekwencje dla zarządzania jakością. Może to oznaczać, że wpływ różnych czynników na jakość produktu lub usługi nie jest jednoznaczny i może wymagać zastosowania innych technik analizy.
Korelacja silna
Jeśli na diagramie korelacji występuje silna korelacja między zmiennymi, można zauważyć pewne charakterystyczne cechy. Przede wszystkim, punkty na diagramie będą tworzyć wyraźny trend, który wskazuje na jednoznaczną zależność między zmiennymi. Rozrzut punktów będzie wąski i skoncentrowany wzdłuż linii trendu.
Przykłady sytuacji, w których silna korelacja może być istotna, to np. zależność między czasem realizacji projektu a ilością zasobów, czy zależność między ceną produktu a poziomem sprzedaży. Silna korelacja może wskazywać na istotne czynniki wpływające na jakość, efektywność lub rentowność.
Konsekwencje silnej korelacji dla zarządzania jakością mogą obejmować konieczność skoncentrowania się na istotnych czynnikach, identyfikację kluczowych wskaźników jakości i dostosowanie działań jakościowych do tych czynników.
Korelacja słaba
Kiedy na diagramie korelacji występuje słaba korelacja między zmiennymi, można zauważyć pewne charakterystyczne cechy. Punkty na diagramie będą rozproszone i nie będą tworzyć jednoznacznej linii trendu. Rozrzut punktów będzie szeroki i nieuporządkowany.
Przykłady sytuacji, w których słaba korelacja może być istotna, to np. zależność między poziomem wykształcenia a zarobkami, czy zależność między wiekiem pracowników a wydajnością. Słaba korelacja może sugerować, że wpływ czynników na jakość jest niewielki lub zmienny.
Ograniczenia interpretacji słabej korelacji wynikają z faktu, że inne czynniki mogą mieć istotny wpływ na zmienną jakość, niezależnie od zależności między badanymi zmiennymi. Dlatego ważne jest, aby uwzględnić inne czynniki i kontekst analizy przy interpretacji słabej korelacji.
Zastosowanie punktowego diagramu korelacji w zarządzaniu jakością
Identyfikacja przyczyn problemów jakościowych
Punktowy diagram korelacji może być użytecznym narzędziem do identyfikacji przyczyn problemów jakościowych. Analiza korelacji między zmiennymi może pomóc w wykrywaniu źródeł wadliwości w procesach produkcyjnych lub świadczenia usług. Na podstawie diagramu korelacji można ustalić, które zmienne mają największy wpływ na jakość i skupić się na ich monitorowaniu i doskonaleniu.
Przykłady sytuacji, w których analiza korelacji może być pomocna w identyfikacji przyczyn problemów jakościowych, to np. zależność między parametrami procesu a wadami produktu, czy zależność między cechami usług a satysfakcją klientów. Analiza korelacji może pomóc w wykrywaniu krytycznych czynników wpływających na jakość i umożliwić podejmowanie odpowiednich działań naprawczych.
Ograniczenia punktowego diagramu korelacji jako narzędzia diagnostycznego wynikają z faktu, że korelacja nie oznacza automatycznie przyczynowości. Istnieje możliwość, że zmienne są skorelowane, ale nie ma między nimi bezpośredniej zależności przyczynowo-skutkowej. Dlatego ważne jest, aby prowadzić dalsze badania i analizy w celu potwierdzenia przyczynowości.
Analiza wpływu czynników na jakość
Punktowy diagram korelacji może być wykorzystany do analizy wpływu różnych czynników na jakość produktu lub usługi. Poprzez analizę korelacji między czynnikami a wskaźnikami jakościowymi, można zidentyfikować, które czynniki mają największy wpływ na jakość i skoncentrować się na ich doskonaleniu.
Przykłady zastosowania analizy korelacji w ocenie wpływu czynników na wskaźniki jakościowe to np. zależność między czynnikami produkcji a wadami produktu, czy zależność między czynnikami obsługi klienta a satysfakcją klientów. Analiza korelacji może pomóc w ustaleniu, które czynniki mają największy wpływ na jakość i umożliwić podejmowanie odpowiednich działań poprawczych.
Jednak analiza korelacji ma pewne potencjalne pułapki i błędy interpretacyjne. Na przykład, korelacja nie oznacza automatycznie przyczynowości, więc ważne jest, aby prowadzić dalsze badania i analizy w celu potwierdzenia przyczynowości. Ponadto, analiza korelacji może nie uwzględniać innych czynników, które mogą mieć wpływ na jakość, takich jak czynniki losowe, błędy ludzkie, czy czynniki społeczne.
Ocena skuteczności działań poprawczych
Punktowy diagram korelacji może być wykorzystany do oceny skuteczności działań poprawczych w procesie doskonalenia jakości. Poprzez analizę korelacji przed i po wprowadzeniu działań poprawczych, można ocenić, czy wprowadzone zmiany miały pozytywny wpływ na jakość.
Przykłady zastosowania analizy korelacji w monitorowaniu efektów działań poprawczych to np. zależność między wprowadzanymi zmianami w procesie a poziomem wad produktu, czy zależność między wprowadzanymi usprawnieniami w obszarze obsługi klienta a satysfakcją klientów. Analiza korelacji może pomóc w ocenie, czy wprowadzone zmiany przyniosły oczekiwane rezultaty i umożliwić dalsze dostosowanie działań jakościowych.
Inne wskaźniki jakości, które mogą być analizowane w kontekście oceny skuteczności działań poprawczych, to np. koszty jakości, wskaźniki wydajności, czy wskaźniki zadowolenia klientów. Ważne jest, aby uwzględnić różne aspekty jakości i dostosować analizę korelacji do konkretnych celów i kontekstu zarządzania jakością.
Wykorzystanie punktowego diagramu korelacji w planowaniu działań jakościowych
Punktowy diagram korelacji może być użytecznym narzędziem w planowaniu działań jakościowych. Analiza korelacji między różnymi zmiennymi może pomóc w identyfikacji obszarów, które wymagają interwencji jakościowej, oraz w ustaleniu priorytetów i celów działań jakościowych.
Przykłady zastosowania diagramu korelacji w planowaniu działań jakościowych to np. zależność między czynnikami produkcji a wadami produktu, czy zależność między czynnikami obsługi klienta a satysfakcją klientów. Analiza korelacji może pomóc w identyfikacji kluczowych obszarów, które mają największy wpływ na jakość i skoncentrować się na nich podczas planowania działań jakościowych.
Potencjalne ograniczenia punktowego diagramu korelacji jako narzędzia planowania jakości wynikają z faktu, że korelacja nie oznacza automatycznie przyczynowości. Istnieje możliwość, że zmienne są skorelowane, ale nie ma między nimi bezpośredniej zależności przyczynowo-skutkowej. Dlatego ważne jest, aby prowadzić dalsze analizy i badania w celu potwierdzenia przyczynowości i dostosować planowanie działań jakościowych do konkretnych potrzeb i kontekstu.
Komunikacja wyników analizy korelacji
Komunikacja wyników analizy korelacji jest kluczowym elementem zarządzania jakością. Istotne jest, aby przedstawić wyniki analizy w sposób zrozumiały dla różnych interesariuszy, takich jak kierownictwo, pracownicy, dostawcy, czy klienci.
Najlepsze praktyki w komunikacji wyników analizy korelacji obejmują dostosowanie języka i formy prezentacji do odbiorców, wykorzystanie grafik i wykresów do wizualizacji wyników, oraz podkreślenie istotnych wniosków i rekomendacji.
Potencjalne pułapki w komunikacji wyników analizy korelacji to np. nadinterpretacja wyników, niedostateczne uwzględnienie innych czynników wpływających na jakość, czy niejednoznaczność przyczynowości. Ważne jest, aby prezentować wyniki analizy korelacji w sposób obiektywny i uwzględniać ich ograniczenia i kontekst.
Przypisy
Bibliografia
- Bachman P. (2017). Jakość w procesach produkcyjnych, "Problemy inżynierii bezpieczeństwa i nauk o pracy", nr 5, s. 46-47
- Krawczyk M. (red.) (2012). Ekonomia eksperymentalna, Wydawnictwo Wolters Kluwer, Warszawa
- Michalski T., (2008). Statystyka, WSiP, Warszawa
- Opolski K., Dykowska G., Możdżonek M. (2003). Zarządzanie przez jakość w usługach zdrowotnych, Wydawnictwo CeDeWu, Warszawa
- Soliński B., (2006).klasyczne narzędzia zarządzania jakością- Diagram korelacji, Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie, Kraków
- Stabryła A. (red.) (2015). Praktyka projektowania systemów organizacyjnych przedsiębiorstwa, Wydawnictwo Mfiles, Kraków
- Steczkowski J., Zeliaś A. (1997). Metody statystyczne w badaniu zjawisk jakościowych, Akademia Ekonomiczna w Krakowie, Kraków
- Wawak S. (2013). Wybrane koncepcje klasyfikacji metod zarządzania jakością, "Zeszyty Naukowe Uniwersytetu Ekonomicznego w Krakowie", nr 910, s. 37-49
- Żebrowska-Łucyk S. (2015). Praktyczne aspekty zastosowania metod statystycznych w procesach systemu zarządzania, "Pomiary Automatyka Robotyka", nr 2, s. 5-12
Autor: Danuta Tomera, Sylwia Bierowiec