Model CAPM

Model CAPM (ang. Capital asset pricing model, model wyceny dóbr kapitałowych) - został opracowany niezależnie przez trzech badaczy: Johna Lintnera (1965), Jana Mossina (1966) i Williama Sharpe'a (1964). Jest to teoria próbująca wyjaśnić wyceny aktywów kapitałowych w kontekście ich ryzyka.

U podstaw podstawowej wersji modelu CAPM leżą następujące założenia (K. Jajuga, 2004, s. 168):

• Inwestorzy są w stanie dokonać wyboru pomiędzy poszczególnymi portfelami na podstawie dwóch charakterystyk: oczekiwanej stopy zwrotu i wariancji.
• Wszyscy inwestorzy posiadają taki sam horyzont inwestycyjny, a ich oczekiwania w stosunku do rozkładu stóp zwrotu z poszczególnych papierów wartościowych są jednorodne.

Rysunek nr 1.Linia rynku kapitałowego CML oraz linia rynku papierów wartościowych SML (Źródło: Jajuga Krzysztof; Jajuga Teresa. Inwestycje, Instrumenty finansowe, Ryzyko finansowe, Inżynieria finansowa. Wydawnictw Naukowe PWN. Warszawa 2004, s. 170)

• Rynek kapitałowy jest rynkiem doskonałym tzn.:
  • brak kosztów transakcyjnych,
  • brak podatków nałożonych na dywidendy, dochody odsetkowe i zyski kapitałowe,
  • brak ograniczeń krótkiej sprzedaży,
  • jest doskonała podzielność instrumentów finansowych,
  • wszystkie instrumenty mogą być bez przeszkód kupowane i sprzedawane na rynku.

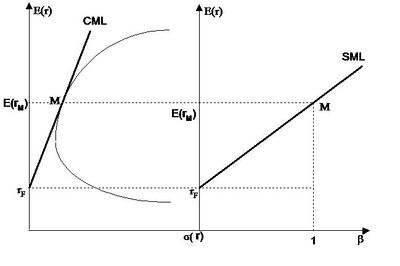
Podstawą CAPM są dwie zależności. Jedna z nich to linia rynku kapitałowego - CML druga natomiast to linia rynków papierów wartościowych - SML. Obie te linie są przedstawione na rysunku poniżej.

TL;DR

Model CAPM to teoria wyceny aktywów kapitałowych oparta na ryzyku. Model ten zakłada, że inwestorzy dokonują wyboru portfeli na podstawie oczekiwanej stopy zwrotu i wariancji. CAPM opiera się na założeniu, że rynek kapitałowy jest doskonały i nie ma kosztów transakcyjnych, podatków ani ograniczeń. Model ten opisuje dwie linie - linia rynku kapitałowego (CML) i linia rynku papierów wartościowych (SML). CML przedstawia zależność między stopą zwrotu a współczynnikiem beta akcji, a SML przedstawia zależność między stopą zwrotu a ryzykiem. Model CAPM ma jednak wiele wad, takich jak nieliniowa zależność, brak jednorodności składnika losowego i niestabilność bety w czasie. Istnieją również rozszerzenia tego modelu, takie jak model zaro-beta CAPM i model ICAPM.

Interpretacja

CML przecina pionową oś układu współrzędnych w punkcie (0, rF). Linia rynku kapitałowego ukazuje graficznie zależność pomiędzy oczekiwaną stopą zwrotu akcji a ich współczynnikami beta. W przestrzeni dochód (R (E (r)) i ryzyko ® można wyznaczyć zależność między oczekiwanymi stopami zwrotu poszczególnych akcji a ich ryzykiem. Ilustruje to linia rynku papierów wartościowych (security market line, SML). Na SML znajdują się w stanie równowagi rynku wszystkie portfele i akcje, natomiast na CML są tylko portfele efektywne. W celu wyznaczenia równania linii rynku papierów wartościowych należy oszacować wyraz wolny i współczynnik kierunkowy.

Wyraz wolny równy jest stopie wolnej od ryzyka (RF) Współczynnik kierunkowy jest ilorazem jednej przyprostokątnej (Rm (E (rm))-RF) do drugiej przyprostokątnej (βM), która równa jest jednostce. Z tego wynika, że współczynnik kierunkowy równa się Rm (E (rM))-RF. Równanie przedstawiające linię rynku papierów wartościowych:

Równanie nr 4. Równanie przedstawiające linię rynku papierów wartościowych (Źródło:Jajuga Krzysztof; Jajuga Teresa. Inwestycje, Instrumenty finansowe, Ryzyko finansowe, Inżynieria finansowa. Wydawnictw Naukowe PWN. Warszawa 2004, s. 169)

$R(E_{r})=R_{F}+R_{M}(E)-R_{F}\beta _{j}$

gdzie:

• R - oczekiwana stopa zwrotu akcji j.
• βj - współczynnik beta tego portfela

Oczekiwana stopa zwrotu z akcji j składa się z stopy zwrotu pozbawionej ryzyka, która ma rekompensować rezygnację z konsumpcji w bieżącym okresie na rzecz konsumpcji w przyszłości, oraz "premii za ryzyko", która wynagradza podjęcie ryzyka związanego z akcją j.

Premia za ryzyko w CAPM

Na "premię za ryzyko" składa się premia za ryzyko związane z portfelem rynkowym (R (E (rM))-RF), czyli nadwyżki oczekiwanej stopy zwrotu z rynku ponad stopę wolną od ryzyka oraz βJ, który koryguje premię za ryzyko w "przeciętny" walor względem ryzyka w akcję J. Warto przeanalizowac kilka przypadków szczególnych, podstawiając do równania różne wartości współczynnika beta (K. Jajuga, 2004, s. 169):

• gdy β=1 (portfel rynkowy), wówczas R=Rm (czyli na SML leży również portfel rynkowy)
• gdy β=0 (instrumenty wolne od ryzyka), wówczas R=Rf (czyli na SML leży portfel zawierający instrumenty wolne od ryzyka)
• gdy β>1 (portfel agresywny), wówczas R>Rm
• gdy 0<β<1 (portfel defensywny), wówczas Rf<R<Rm
• gdy β<0, wówczas R<Rf.

Rodzaje portfeli w CAPM

• portfele dobrze wycenione - to portfele leżące na SML, oznacza to że spodziewana stopa zwrotu jest równa stopie zwrotu wynikającej z SML
• portfel niedowartościowany(underpriced) - to portfele leżące powyżej SML, spodziewana stopa zwrotu jest wyższa niż stopa zwrotu, jaką zyskuje z portfela o takim samym współczynniku beta w warunkach równowagi. Jest to portfel atrakcyjny dla inwestorów, dlatego też będą się starali o kupno. Spowoduje to wzrost ceny, co wywoła spadek stopy zwrotu. W rezultacie czego dany portfel osiągnie potrzebną pozycję leżąco na SML.
• portfel przewartościowany (overpriced) - jest to portfel który leży poniżej SML oznacza to, że spodziewana stopa zwrotu jest niższa od stopy zwrotu, jaką w warunkach równowagi można osiągnąć z portfela o takim samym współczynniku beta. Portfel ten nie jest atrakcyjny, dlatego inwestorzy będą usiłować sprzedać dany portfel. W efekcie czego cena spadnie co spowoduje wzrost stopy zwrotu. W efekcie końcowym spowoduje to, że portfel w warunkach równowagi uzyska odpowiednie miejsce na SML.

Model CAMP standardowo traktowany jest jak model wyceny, jednak całe rozumowanie jest przeprowadzone w kategoriach stopy zwrotu. Istnieje bezpośredni związek między ceną a stopą zwrotu m.in.:

• jeśli stopa zwrotu jest wyższa niż stopa zwrotu, która wynika z wyceny, oznacza to, że cena jest niższa,
• jeśli stopa zwrotu jest niższa niż stopa zwrotu, która wynika z wyceny, oznacza że cena jest wyższa

Wady modelu CAPM

Klasyczny model wyceny aktywów kapitałowych ma swoich zwolenników ale również przeciwników. Przeprowadzone badania w Center for Research on Security Prices nie pokazały jednoznacznych wniosków odnoście poprawności tego modelu oraz oceny współczynnika beta.

Model CAPM zostaje bardzo popularnym modelem. Jednak posiada liczne wady:

• potrzeby uzupełniania modelu o dodatkowe zmienne, które oprócz ryzyka systematycznego, wpływają na poziom stóp zwrotu,
• nieliniowy charakter zależności w równaniu,
• brak jednorodności składnika losowego,
• błędy pomiarów zmiennych,
• brak stabilności bety w czasie

Rozszerzenia modelu CAPM

Dokonano wiele modyfikacji i rozszerzeń modelu CAMP m.in.:

Model zaro-beta CAPM Model ten stworzony został przez Fishera Blacka. Model ten uwzględnia sytuację kiedy na rynku nie ma instrumentu wolnego od ryzyka ale istnieje portfel akcji, którego współczynnik beta jest równy 0. Postać tego modelu jest podobna do klasycznego modelu CAPM, z tym, że stopa wolna od ryzyka jest zamieniona na stopę zwrotu portfela akcji o współczynniku beta równym 0. W praktyce oczekiwana stopa zwrotu portfela akcji o współczynniku beta 0 jest wyższa niż stopa wolna od ryzyka co powoduję, że linia SML wyznaczona w tym modelu ma mniejsze nachyleni niż klasyczna linia SML.

Model ICAPM (International CAPM) Jest to model dla inwestycji międzynarodowych. Model ten wprowadza 2 modyfikacje w stosunku do klasycznego CAPM: portfelem rynkowym jest globalny portfel, uwzględniane są premie za ryzyko kursów walut.

Model CAPM — artykuły polecane

Teoria arbitrażu cenowego — Teoria Markowitza — Rynek efektywny — Cena emisyjna — Stopa zwrotu — Model Blacka Scholesa — Premia za ryzyko — Stopa wolna od ryzyka — Kurs akcji

Bibliografia

• Czapiewski L. (2015), Model CAPM i trójczynnikowy model Famy-Frencha w analizie zdarzeń na polskim rynku kapitałowym, Zeszyty Naukowe Uniwersytetu Szczecińskiego Finanse, Rynki Finansowe, Ubezpieczenia, Nr 73
• Jajuga K., Jajuga T. (2012), Inwestycje: instrumenty finansowe, aktywa niefinansowe, ryzyko finansowe, inżynieria finansowa, Wydawnictwo Naukowe PWN, Warszawa
• Jajuga K., Jajuga T. (2012), Inwestycje: instrumenty finansowe, aktywa niefinansowe, ryzyko finansowe, inżynieria finansowa, Wydawnictwo Naukowe PWN, Warszawa
• Piotrowski S. (2015), Model CAPM z ryzykiem płynności na polskim rynku kapitałowym, Zeszyty Naukowe Uniwersytetu Szczecińskiego. Współczesne Problemy Ekonomiczne, Nr 11
• Tarczyński W., Witkowska D., Kompa K. (2013), Współczynnik Beta. Teoria i praktyka, Pielaszek Research, Warszawa

Autor: Bolesław Zieleń, Angelika Pryszlak