PERT: Różnice pomiędzy wersjami
m (Infobox update) |
(LinkTitles.) |
||
| Linia 16: | Linia 16: | ||
'''PERT''' to probabilistyczna metoda planowania i kontroli projektu. Skrót pochodzi od angielskiej nazwy Project Evaluation and Review Technique (w niektórych źródłach "project” jest zastąpione słowem "program”). Metoda PERT w formie graficznej jest oparta na diagramie kierunkowym o [[notacja AoA|notacji AoA]] (Activity on Arrows) lub AoN (Activity on Nodes). Podobnie jak metoda ścieżki krytycznej [[CPM]] (ang. Critical Path Method) pozwala określić drogę krytyczną, najwcześniejsze i najpóźniejsze czasy poszczególnych zdarzeń, a także zapasy czasu na poszczególnych zadaniach. W przypadku tej metody, parametry te nie są podawane jako wielkości pewne i jednoznacznie określone (jak w przypadku CPM), ale jako zmienne losowe o określonej krzywej gęstości prawdopodobieństwa. Estymacja na bazie trzech danych probabilistycznych (najkrótszy, najdłuższy oraz najbardziej prawdopodobny czas wykonania danej czynności) pozwala na bardzo precyzyjne określenie czasów trwania poszczególnych zadań i terminu zakończenia projektu. Metoda PERT jest szczególnie użyteczna w zarządzaniu projektami o charakterze badawczo-rozwojowym, gdzie deterministyczne określenie czasów czynności jest na ogół trudne, a niejednokrotnie wręcz niemożliwe. | '''PERT''' to probabilistyczna [[metoda]] planowania i kontroli projektu. Skrót pochodzi od angielskiej nazwy Project Evaluation and Review Technique (w niektórych źródłach "project” jest zastąpione słowem "program”). Metoda PERT w formie graficznej jest oparta na diagramie kierunkowym o [[notacja AoA|notacji AoA]] (Activity on Arrows) lub AoN (Activity on Nodes). Podobnie jak metoda ścieżki krytycznej [[CPM]] (ang. Critical Path Method) pozwala określić drogę krytyczną, najwcześniejsze i najpóźniejsze czasy poszczególnych zdarzeń, a także [[zapasy]] czasu na poszczególnych zadaniach. W przypadku tej metody, parametry te nie są podawane jako wielkości pewne i jednoznacznie określone (jak w przypadku CPM), ale jako zmienne losowe o określonej krzywej gęstości prawdopodobieństwa. [[Estymacja]] na bazie trzech danych probabilistycznych (najkrótszy, najdłuższy oraz najbardziej prawdopodobny czas wykonania danej czynności) pozwala na bardzo precyzyjne określenie czasów trwania poszczególnych zadań i terminu zakończenia projektu. Metoda PERT jest szczególnie użyteczna w zarządzaniu projektami o charakterze badawczo-rozwojowym, gdzie deterministyczne określenie czasów czynności jest na ogół trudne, a niejednokrotnie wręcz niemożliwe. | ||
<google>t</google> | <google>t</google> | ||
==Historia== | ==Historia== | ||
Metoda PERT została opracowana w latach 1956-58 w celu uproszczenia procedur planowania i harmonogramowania dużych i skomplikowanych projektów. Biuro Projektów Specjalnych Marynarki Wojennej USA (ang. U.S. Navy Special Projects Office) zleciło opracowanie nowej metody [[zarządzanie czasem|zarządzania czasem]] na potrzeby programu atomowych okrętów podwodnych Polaris (Malcolm D. i in. 1959, s. 646-669). Od tego czasu jest bardzo szeroko stosowana w przypadku bardzo dużych i skomplikowanych projektów. Pierwotnie metoda została opracowana jako system komputerowy, dopiero później zaczęto stosować zapis graficzny. | Metoda PERT została opracowana w latach 1956-58 w celu uproszczenia procedur planowania i harmonogramowania dużych i skomplikowanych projektów. Biuro Projektów Specjalnych Marynarki Wojennej USA (ang. U.S. Navy Special Projects Office) zleciło opracowanie nowej metody [[zarządzanie czasem|zarządzania czasem]] na [[potrzeby]] programu atomowych okrętów podwodnych Polaris (Malcolm D. i in. 1959, s. 646-669). Od tego czasu jest bardzo szeroko stosowana w przypadku bardzo dużych i skomplikowanych projektów. Pierwotnie metoda została opracowana jako [[system]] komputerowy, dopiero później zaczęto stosować [[zapis]] graficzny. | ||
Spektakularnym przykładem zastosowania metody PERT były przygotowania do Olimpiady Zimowej w Grenoble (1968) – realizacja projektu trwała od 1965 roku, aż do chwili otwarcia igrzysk (1968 Winter Olympics official report. 2005, s. 47-51). | Spektakularnym przykładem zastosowania metody PERT były przygotowania do Olimpiady Zimowej w Grenoble (1968) – realizacja projektu trwała od 1965 roku, aż do chwili otwarcia igrzysk (1968 Winter Olympics official report. 2005, s. 47-51). | ||
| Linia 27: | Linia 27: | ||
==Tworzenie diagramu sieciowego PERT== | ==Tworzenie diagramu sieciowego PERT== | ||
{{#ev:youtube|M_tFsoxwnNE|480|right|Wykresy sieciowe (Sławomir Wawak)|frame}} | {{#ev:youtube|M_tFsoxwnNE|480|right|Wykresy sieciowe (Sławomir Wawak)|frame}} | ||
Metoda PERT opiera się na stworzeniu [[diagram strzałkowy|diagramu strzałkowego]] uwzględniającego relacje między poszczególnymi zadaniami i nadrzędność zadań względem siebie. Diagram jest najczęściej tworzony przy użyciu notacji AoN - Activity on Nodes gdzie zadania przedstawiane są w postaci prostokątów (węzłów) połączonych strzałkami. W węźle wpisuje się wszystkie dane i dokonuje obliczeń. Zamiennie może być również stosowana notacja AoA (Activity on Arrows), jednak jest ona obecnie rzadko stosowana ze względu na niektóre swoje cechy (np. konieczność wprowadzania czynności pozornych). | Metoda PERT opiera się na stworzeniu [[diagram strzałkowy|diagramu strzałkowego]] uwzględniającego relacje między poszczególnymi zadaniami i nadrzędność zadań względem siebie. Diagram jest najczęściej tworzony przy użyciu notacji AoN - Activity on Nodes gdzie zadania przedstawiane są w postaci prostokątów (węzłów) połączonych strzałkami. W węźle wpisuje się wszystkie [[dane]] i dokonuje obliczeń. Zamiennie może być również stosowana [[notacja AoA]] (Activity on Arrows), jednak jest ona obecnie rzadko stosowana ze względu na niektóre swoje cechy (np. konieczność wprowadzania czynności pozornych). | ||
Każdy prostokąt obrazujący zadanie lub czynność zawiera następujące informacje: | Każdy prostokąt obrazujący [[zadanie]] lub czynność zawiera następujące [[informacje]]: | ||
* numer identyfikacyjny i opis zadania, | * numer identyfikacyjny i opis zadania, | ||
* najwcześniejszy i najpóźniejszy termin rozpoczęcia ''(ang. ES-Early Start oraz EF-Early Finish)'', | * najwcześniejszy i najpóźniejszy termin rozpoczęcia ''(ang. ES-Early Start oraz EF-Early Finish)'', | ||
* najwcześniejszy i najpóźniejszy termin zakończenia ''(ang. LS-Late Start oraz LF-Late Finish)'', | * najwcześniejszy i najpóźniejszy termin zakończenia ''(ang. LS-Late Start oraz LF-Late Finish)'', | ||
* czas trwania zadania ''(ang. D-Duration)'', | * czas trwania zadania ''(ang. D-Duration)'', | ||
* całkowity zapas czasu ''(ang. F-Float)''. | * całkowity [[zapas]] czasu ''(ang. F-Float)''. | ||
Tradycyjny układ notacji, pochodzący z francuskiej metody MPM (ang. Metra Potential Method) w diagramie PERT przedstawiono na rysunku. | Tradycyjny układ notacji, pochodzący z francuskiej metody MPM (ang. Metra Potential Method) w diagramie PERT przedstawiono na rysunku. | ||
| Linia 49: | Linia 49: | ||
==Określanie czasu trwania zadań== | ==Określanie czasu trwania zadań== | ||
W celu określenia czasu trwania każdego z zadań, należy określić trzy wartości – warianty czasu wykonania: | W celu określenia czasu trwania każdego z zadań, należy określić trzy wartości – [[warianty]] czasu wykonania: | ||
::'''t<sub>a</sub>''' – najkrótszy możliwy (in. optymistyczny) czas trwania danej czynności (wystąpi w warunkach szczególnie korzystnych dla realizacji zadania), | ::'''t<sub>a</sub>''' – najkrótszy możliwy (in. optymistyczny) czas trwania danej czynności (wystąpi w warunkach szczególnie korzystnych dla realizacji zadania), | ||
::'''t<sub>b</sub>''' – najdłuższy możliwy (in. pesymistyczny) czas trwania danej czynności (wystąpi w przypadku szeregu trudności powodujących opóźnienie realizacji zadania), | ::'''t<sub>b</sub>''' – najdłuższy możliwy (in. pesymistyczny) czas trwania danej czynności (wystąpi w przypadku szeregu trudności powodujących opóźnienie realizacji zadania), | ||
| Linia 65: | Linia 65: | ||
<math>t_e=\frac{t_a+4t_m+t_b}{6}</math> | <math>t_e=\frac{t_a+4t_m+t_b}{6}</math> | ||
Następnie obliczamy odchylenie standardowe i wariancję czasu realizacji zadania wg poniższych wzorów: | Następnie obliczamy [[odchylenie standardowe]] i wariancję czasu realizacji zadania wg poniższych wzorów: | ||
odchylenie standardowe: <math>δ_t=\frac{t_a+t_b}{6}</math>, | odchylenie standardowe: <math>δ_t=\frac{t_a+t_b}{6}</math>, | ||
wariancja: <math>δ_t^2=\left (\frac{t_b-t_a}{6}\right)^2</math> | [[wariancja]]: <math>δ_t^2=\left (\frac{t_b-t_a}{6}\right)^2</math> | ||
Wszystkie wyznaczone i obliczone parametry należy umieścić w tabeli co znacznie ułatwi ich wstępną analizę. | Wszystkie wyznaczone i obliczone parametry należy umieścić w tabeli co znacznie ułatwi ich wstępną analizę. | ||
| Linia 74: | Linia 74: | ||
==Wstępna analiza parametrów czasu realizacji zadań== | ==Wstępna analiza parametrów czasu realizacji zadań== | ||
Różne wartości parametrów ta, tm i tb mogą dawać tę samą wartość czasu przeciętnego. Należy pamiętać, że czas pesymistyczny i optymistyczny są określane subiektywnie przez członków [[zespół projektowy|zespołu projektowego]]. Subiektywne oceny czasu realizacji tego samego zadania mogą być zatem bardzo rozbieżne, w zależności od nastawienia osoby oceniającej. Dlatego też wstępna analiza jest niezmiernie istotna. | Różne wartości parametrów ta, tm i tb mogą dawać tę samą [[wartość]] czasu przeciętnego. Należy pamiętać, że czas pesymistyczny i optymistyczny są określane subiektywnie przez członków [[zespół projektowy|zespołu projektowego]]. Subiektywne oceny czasu realizacji tego samego zadania mogą być zatem bardzo rozbieżne, w zależności od nastawienia osoby oceniającej. Dlatego też wstępna analiza jest niezmiernie istotna. | ||
Przykład (Bladowski 1970, s. 136): | Przykład (Bladowski 1970, s. 136): | ||
| Linia 98: | Linia 98: | ||
Podstawowym celem analizy diagramu PERT jest określenie najkrótszego czasu ukończenia projektu, z uwzględnieniem wszelkich ograniczeń, zależności logicznych i estymowanego czasu trwania poszczególnych czynności. | Podstawowym celem analizy diagramu PERT jest określenie najkrótszego czasu ukończenia projektu, z uwzględnieniem wszelkich ograniczeń, zależności logicznych i estymowanego czasu trwania poszczególnych czynności. | ||
Rozwiązując sieć metodą PERT, podobnie jak zresztą w przypadku innych metod sieciowych, należy pamiętać o probabilistycznym charakterze tych metod. Cały tworzony diagram opiera się najczęściej na subiektywnych ocenach członków zespołu (szczególnie w przypadku niepowtarzalnych projektów o charakterze badawczo-rozwojowym). W związku z tym, cała analiza, jak i jej wyniki mają charakter probabilistyczny. Jedynie w niektórych przypadkach, gdy opieramy się na danych historycznych lub porównawczych (dane dotyczące podobnych zadań wykonanych w toku realizacji innych projektów) wynik jest bliższy rzeczywistości. Ale przy pracy nad takimi projektami częściej stosuje się metodę CPM. | Rozwiązując sieć metodą PERT, podobnie jak zresztą w przypadku innych metod sieciowych, należy pamiętać o probabilistycznym charakterze tych metod. Cały tworzony diagram opiera się najczęściej na subiektywnych ocenach członków zespołu (szczególnie w przypadku niepowtarzalnych projektów o charakterze badawczo-rozwojowym). W związku z tym, cała analiza, jak i jej wyniki mają charakter probabilistyczny. Jedynie w niektórych przypadkach, gdy opieramy się na danych historycznych lub porównawczych (dane dotyczące podobnych zadań wykonanych w toku realizacji innych projektów) [[wynik]] jest bliższy rzeczywistości. Ale przy pracy nad takimi projektami częściej stosuje się metodę CPM. | ||
===Pierwszy etap - analiza "do przodu"=== | ===Pierwszy etap - analiza "do przodu"=== | ||
| Linia 125: | Linia 125: | ||
Wśród najważniejszych zalet metody PERT możemy wymienić: | Wśród najważniejszych zalet metody PERT możemy wymienić: | ||
* nadaje się do zarządzania dużymi, skomplikowanymi projektami, | * nadaje się do zarządzania dużymi, skomplikowanymi projektami, | ||
*łatwość obliczeń zmniejsza ryzyko popełnienia błędów, | *łatwość obliczeń zmniejsza [[ryzyko]] popełnienia błędów, | ||
* graficzna, przejrzysta prezentacja pozwala łatwo zdefiniować powiązania pomiędzy poszczególnymi zadaniami oraz określić ścieżkę krytyczną, | * graficzna, przejrzysta prezentacja pozwala łatwo zdefiniować powiązania pomiędzy poszczególnymi zadaniami oraz określić ścieżkę krytyczną, | ||
* prezentacja graficzna ułatwia i przyspiesza procesy decyzyjne, | * prezentacja graficzna ułatwia i przyspiesza procesy decyzyjne, | ||
| Linia 141: | Linia 141: | ||
* Malcolm, D. G., J. H. Roseboom, C. E. Clark, W. Fazar 1959. [http://mech.vub.ac.be/teaching/info/Ontwerpmethodologie/Appendix%20les%202%20PERT.pdf ''Application of a Technique for Research and Development Program Evaluation'']. OPERATIONS RESEARCH Vol. 7, No. 5, s. 646–669 | * Malcolm, D. G., J. H. Roseboom, C. E. Clark, W. Fazar 1959. [http://mech.vub.ac.be/teaching/info/Ontwerpmethodologie/Appendix%20les%202%20PERT.pdf ''Application of a Technique for Research and Development Program Evaluation'']. OPERATIONS RESEARCH Vol. 7, No. 5, s. 646–669 | ||
* Połoński M. (2005), ''[http://mieczyslaw_polonski.users.sggw.pl/Acta2005.pdf Rozkład czasu trwania czynności a termin zakończenia przedsięwzięcia z uwzględnieniem elementów analizy ryzyka.]'' ACTA Scientiarum Polonorum. Archtectura, 4(2). | * Połoński M. (2005), ''[http://mieczyslaw_polonski.users.sggw.pl/Acta2005.pdf Rozkład czasu trwania czynności a termin zakończenia przedsięwzięcia z uwzględnieniem elementów analizy ryzyka.]'' ACTA Scientiarum Polonorum. Archtectura, 4(2). | ||
* Project Management Institute, ''Guide to the Project Management Body of Knowledge (PMBOK® Guide).'', Fifth edition, wydanie angielskie, Management Training & Development Centre, Warszawa 2013 | * [[Project Management Institute]], ''Guide to the Project Management Body of Knowledge (PMBOK® Guide).'', Fifth edition, wydanie angielskie, Management Training & Development Centre, Warszawa 2013 | ||
* 1968 ''[http://library.la84.org/6oic/OfficialReports/1968/or1968.pdf Winter Olympics official report]'' (2005), wersja elektroniczna w języku angielskim, Amateur Athletic Foundation of Los Angeles, s. 47-51 | * 1968 ''[http://library.la84.org/6oic/OfficialReports/1968/or1968.pdf Winter Olympics official report]'' (2005), wersja elektroniczna w języku angielskim, Amateur Athletic Foundation of Los Angeles, s. 47-51 | ||
Wersja z 00:29, 21 maj 2020
| PERT |
|---|
| Polecane artykuły |
PERT to probabilistyczna metoda planowania i kontroli projektu. Skrót pochodzi od angielskiej nazwy Project Evaluation and Review Technique (w niektórych źródłach "project” jest zastąpione słowem "program”). Metoda PERT w formie graficznej jest oparta na diagramie kierunkowym o notacji AoA (Activity on Arrows) lub AoN (Activity on Nodes). Podobnie jak metoda ścieżki krytycznej CPM (ang. Critical Path Method) pozwala określić drogę krytyczną, najwcześniejsze i najpóźniejsze czasy poszczególnych zdarzeń, a także zapasy czasu na poszczególnych zadaniach. W przypadku tej metody, parametry te nie są podawane jako wielkości pewne i jednoznacznie określone (jak w przypadku CPM), ale jako zmienne losowe o określonej krzywej gęstości prawdopodobieństwa. Estymacja na bazie trzech danych probabilistycznych (najkrótszy, najdłuższy oraz najbardziej prawdopodobny czas wykonania danej czynności) pozwala na bardzo precyzyjne określenie czasów trwania poszczególnych zadań i terminu zakończenia projektu. Metoda PERT jest szczególnie użyteczna w zarządzaniu projektami o charakterze badawczo-rozwojowym, gdzie deterministyczne określenie czasów czynności jest na ogół trudne, a niejednokrotnie wręcz niemożliwe.
Historia
Metoda PERT została opracowana w latach 1956-58 w celu uproszczenia procedur planowania i harmonogramowania dużych i skomplikowanych projektów. Biuro Projektów Specjalnych Marynarki Wojennej USA (ang. U.S. Navy Special Projects Office) zleciło opracowanie nowej metody zarządzania czasem na potrzeby programu atomowych okrętów podwodnych Polaris (Malcolm D. i in. 1959, s. 646-669). Od tego czasu jest bardzo szeroko stosowana w przypadku bardzo dużych i skomplikowanych projektów. Pierwotnie metoda została opracowana jako system komputerowy, dopiero później zaczęto stosować zapis graficzny.
Spektakularnym przykładem zastosowania metody PERT były przygotowania do Olimpiady Zimowej w Grenoble (1968) – realizacja projektu trwała od 1965 roku, aż do chwili otwarcia igrzysk (1968 Winter Olympics official report. 2005, s. 47-51).
Tworzenie diagramu sieciowego PERT
{{#ev:youtube|M_tFsoxwnNE|480|right|Wykresy sieciowe (Sławomir Wawak)|frame}} Metoda PERT opiera się na stworzeniu diagramu strzałkowego uwzględniającego relacje między poszczególnymi zadaniami i nadrzędność zadań względem siebie. Diagram jest najczęściej tworzony przy użyciu notacji AoN - Activity on Nodes gdzie zadania przedstawiane są w postaci prostokątów (węzłów) połączonych strzałkami. W węźle wpisuje się wszystkie dane i dokonuje obliczeń. Zamiennie może być również stosowana notacja AoA (Activity on Arrows), jednak jest ona obecnie rzadko stosowana ze względu na niektóre swoje cechy (np. konieczność wprowadzania czynności pozornych).
Każdy prostokąt obrazujący zadanie lub czynność zawiera następujące informacje:
- numer identyfikacyjny i opis zadania,
- najwcześniejszy i najpóźniejszy termin rozpoczęcia (ang. ES-Early Start oraz EF-Early Finish),
- najwcześniejszy i najpóźniejszy termin zakończenia (ang. LS-Late Start oraz LF-Late Finish),
- czas trwania zadania (ang. D-Duration),
- całkowity zapas czasu (ang. F-Float).
Tradycyjny układ notacji, pochodzący z francuskiej metody MPM (ang. Metra Potential Method) w diagramie PERT przedstawiono na rysunku.
| Najwcześniejsze rozpoczęcie | Czas trwania zadania | Najwcześniejsze zakończenie |
| Numer identyfikacyjny i opis zadania | ||
| Najpóźniejsze rozpoczęcie | Całkowity zapas czasu | Najpóźniejsze zakończenie |
Określanie czasu trwania zadań
W celu określenia czasu trwania każdego z zadań, należy określić trzy wartości – warianty czasu wykonania:
- ta – najkrótszy możliwy (in. optymistyczny) czas trwania danej czynności (wystąpi w warunkach szczególnie korzystnych dla realizacji zadania),
- tb – najdłuższy możliwy (in. pesymistyczny) czas trwania danej czynności (wystąpi w przypadku szeregu trudności powodujących opóźnienie realizacji zadania),
- tm – najbardziej prawdopodobny (in. realistyczny) czas trwania danej czynności (ta < tm < tb).
Do obliczenia oczekiwanego czasu realizacji zadania możemy posłużyć się trójkątnym rozkładem gęstości prawdopodobieństwa. Wówczas należałoby posłużyć się wzorem:
Jednak metoda PERT w wersji klasycznej przyjmuje rozkład beta krzywej gęstości prawdopodobieństwa. Wybierając ten rozkład, twórcy metody opierali się bardziej na intuicji niż wiedzy, co nie umniejsza dużej wartości praktycznej metody PERT (Bladowski 1970, s. 135]).
W celu obliczenia oczekiwanego czasu realizacji zadania wg rozkładu beta, posługujemy się wzorem:
Następnie obliczamy odchylenie standardowe i wariancję czasu realizacji zadania wg poniższych wzorów:
odchylenie standardowe: Parser nie mógł rozpoznać (błąd składni): {\displaystyle δ_t=\frac{t_a+t_b}{6}} , wariancja: Parser nie mógł rozpoznać (błąd składni): {\displaystyle δ_t^2=\left (\frac{t_b-t_a}{6}\right)^2}
Wszystkie wyznaczone i obliczone parametry należy umieścić w tabeli co znacznie ułatwi ich wstępną analizę.
Wstępna analiza parametrów czasu realizacji zadań
Różne wartości parametrów ta, tm i tb mogą dawać tę samą wartość czasu przeciętnego. Należy pamiętać, że czas pesymistyczny i optymistyczny są określane subiektywnie przez członków zespołu projektowego. Subiektywne oceny czasu realizacji tego samego zadania mogą być zatem bardzo rozbieżne, w zależności od nastawienia osoby oceniającej. Dlatego też wstępna analiza jest niezmiernie istotna.
Przykład (Bladowski 1970, s. 136): Trzy osoby A, B i C podały własne oceny tej samej czynności, różniące się parametrami a, m, b:
| Osoba | ta | tm | tb | te | δt | δ2t |
| A | 5 | 10 | 15 | 10 | 1,65 | 2,72 |
| B | 3 | 8 | 25 | 10 | 3,56 | 12,67 |
| C | 2 | 7 | 30 | 10 | 4,70 | 22,09 |
We wszystkich przypadkach, wartość czasów oczekiwanych (te) jest identyczna, jednak wartości odchylenia standardowego i wariancji wskazują na znaczną różnicę w ocenie sytuacji przez osoby A, B i C. Osoba A, dla której wartość odchylenia standardowego wynosi 1,65 oceniła czas realizacji zadania bardzo precyzyjnie. Tymczasem osoba C (wartość δt=4,7) wykazała dużą ostrożność.
Powtarzające się duże wartości wariancji i odchylenia standardowego będą świadczyły o dużej niepewności w ocenie czasu realizacji zadań oraz końcowego terminu realizacji projektu. Krótko mówiąc – im niższe wartości wariancji i odchylenia standardowego – tym lepiej.
Rozwiązywanie sieci zadań metodą PERT
Podstawowym celem analizy diagramu PERT jest określenie najkrótszego czasu ukończenia projektu, z uwzględnieniem wszelkich ograniczeń, zależności logicznych i estymowanego czasu trwania poszczególnych czynności.
Rozwiązując sieć metodą PERT, podobnie jak zresztą w przypadku innych metod sieciowych, należy pamiętać o probabilistycznym charakterze tych metod. Cały tworzony diagram opiera się najczęściej na subiektywnych ocenach członków zespołu (szczególnie w przypadku niepowtarzalnych projektów o charakterze badawczo-rozwojowym). W związku z tym, cała analiza, jak i jej wyniki mają charakter probabilistyczny. Jedynie w niektórych przypadkach, gdy opieramy się na danych historycznych lub porównawczych (dane dotyczące podobnych zadań wykonanych w toku realizacji innych projektów) wynik jest bliższy rzeczywistości. Ale przy pracy nad takimi projektami częściej stosuje się metodę CPM.
Pierwszy etap - analiza "do przodu"
Pierwszym etapem jest obliczenie najwcześniejszego możliwego zakończenia projektu, co w praktyce oznacza obliczenie tego parametru dla ostatniego zadania w diagramie (patrząc od lewej do prawej). Rozpoczynamy od najwcześniejszego rozpoczęcia zadania nr 1 (czyli 0) i dodajemy oczekiwany czas trwania tego zadania. W wyniku otrzymujemy najwcześniejszy możliwy czas zakończenia zadania, który jest jednocześnie najwcześniejszym możliwym czasem rozpoczęcia kolejnego. Analogicznie postępujemy aż do ostatniego zadania w diagramie.
Tradycyjnie jako czas rozpoczęcia pierwszego zadania wpisywano "1" - pierwszy dzień trwania projektu. Powodowało to jednak komplikacje w dalszych obliczeniach, dlatego też współcześnie zaczyna się raczej od "0". Niemniej obie metody są prawidłowe.
UWAGA – w sytuacji, gdy do jednego zadania prowadzą dwie ścieżki w relacji "koniec-start", obie ścieżki muszą się zakończyć, aby zadanie mogło wystąpić. Jako początek kolejnego zadania przyjmujemy zatem koniec dłuższej z nich.
Drugi etap - analiza "wstecz"
Celem drugiego etapu jest określenie zapasów czasu dla każdego zadania. Całkowity zapas czasu to o jaki możemy opóźnić rozpoczęcie realizacji danego zadania, nie powodując opóźnienia realizacji następnego. Zadania pierwsze i ostatnie zawsze mają zerowy zapas czasu.
Obliczenia rozpoczynamy tym razem od ostatniego zadania. Najwcześniejszy czas zakończenia zadania (obliczony w pierwszym etapie) jest jednocześnie najpóźniejszym czasem jego zakończenia. Od tej wartości odejmujemy oczekiwany czas trwania zadania. Wynik jest najpóźniejszym czasem rozpoczęcia. Analogicznie postępujemy z kolejnymi zadaniami, poruszając się wzdłuż powiązań logicznych, od prawej do lewej, aż do zadania początkowego.
UWAGA – analogicznie do obliczeń w pierwszym etapie, jako najpóźniejszy czas zakończenia zadania do którego prowadzą dwie ścieżki w relacji "koniec-start", przyjmujemy najpóźniejszy czas rozpoczęcia poprzedniego zadania na dłuższej ścieżce. Analizujemy od prawej do lewej, a więc "poprzednie zadanie" oznacza w tym przypadku zadanie po prawej stronie od zadania analizowanego.
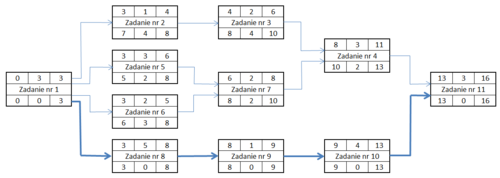
Przykładowy diagram PERT
Rys. 1. Przykład wykresu PERT w notacji AoN
Ścieżka krytyczna
Po obliczeniu najwcześniejszego możliwego terminu zakończenia projektu i określeniu zapasów czasu dla poszczególnych zadań, zawsze pojawi się przynajmniej jeden łańcuch czynności z zerowym zapasem czasu. Są to czynności o strategicznym znaczeniu dla realizacji całego projektu, gdyż jakiekolwiek opóźnienie w ich wykonaniu spowoduje opóźnienie zakończenia całego projektu. Na rysunku ścieżka krytyczna została zaznaczona pogrubionymi strzałkami.
Zalety metody PERT
Wśród najważniejszych zalet metody PERT możemy wymienić:
- nadaje się do zarządzania dużymi, skomplikowanymi projektami,
- łatwość obliczeń zmniejsza ryzyko popełnienia błędów,
- graficzna, przejrzysta prezentacja pozwala łatwo zdefiniować powiązania pomiędzy poszczególnymi zadaniami oraz określić ścieżkę krytyczną,
- prezentacja graficzna ułatwia i przyspiesza procesy decyzyjne,
- w sposób przejrzysty pokazuje zapasy czasu na poszczególnych zadaniach.
Wady metody PERT
Metoda PERT ma jednak również pewne wady. Najistotniejsze z nich to:
- nieefektywna w przypadku małych projektów,
- graficzna prezentacja diagramu z reguły zajmuje dużą powierzchnię, przez co jest niewygodna,
- konstrukcja diagramu nie pozwala na łatwą i przejrzystą prezentację etapu realizacji projektu.
Bibliografia
- Bladowski S. (1970), Metody sieciowe w planowaniu i organizacji pracy. PWE Warszawa
- Lock D. (2009), Podstawy zarządzania projektami. PWE Warszawa
- Malcolm, D. G., J. H. Roseboom, C. E. Clark, W. Fazar 1959. Application of a Technique for Research and Development Program Evaluation. OPERATIONS RESEARCH Vol. 7, No. 5, s. 646–669
- Połoński M. (2005), Rozkład czasu trwania czynności a termin zakończenia przedsięwzięcia z uwzględnieniem elementów analizy ryzyka. ACTA Scientiarum Polonorum. Archtectura, 4(2).
- Project Management Institute, Guide to the Project Management Body of Knowledge (PMBOK® Guide)., Fifth edition, wydanie angielskie, Management Training & Development Centre, Warszawa 2013
- 1968 Winter Olympics official report (2005), wersja elektroniczna w języku angielskim, Amateur Athletic Foundation of Los Angeles, s. 47-51
Autor: Michał Imianowski