MPM: Różnice pomiędzy wersjami
m (Infobox update) |
(LinkTitles.) |
||
| Linia 15: | Linia 15: | ||
'''Metra Potential Method''' (MPM) to narzędzie do zarządzania projektami, opracowane w 1958 roku przez francuza Bernarda Roya. Narzędzie to służy do '''opisywania, organizowania i planowania zadań''', które stanowią rozwój projektu. Metoda ta jest podobna do metody PERT. Wierzchołki pokazują zadania, a połączenia przedstawiają ograniczenie pierwszeństwa zadań. | '''Metra Potential Method''' (MPM) to narzędzie do zarządzania projektami, opracowane w 1958 roku przez francuza Bernarda Roya. Narzędzie to służy do '''opisywania, organizowania i planowania zadań''', które stanowią [[rozwój]] projektu. [[Metoda]] ta jest podobna do metody PERT. Wierzchołki pokazują zadania, a połączenia przedstawiają ograniczenie pierwszeństwa zadań. | ||
== Historia == | == Historia == | ||
| Linia 24: | Linia 24: | ||
== Koncepcja== | == Koncepcja== | ||
[[Plik:Symbol zadania w MPM.jpg|400px|thumb|Rys. 1. Symbol zadania w MPM]] | [[Plik:Symbol zadania w MPM.jpg|400px|thumb|Rys. 1. Symbol zadania w MPM]] | ||
MPM została stworzona w tym samym oku co metoda PERT. Jest ona metodą reprezentacji i optymalizacji zadań projektowych. Można ją uznać za połowę drogi między wykresem Gantta a reprezentacja PERT. Pozwala ona na nadanie pierwszeństwa dużej ilości zadań biorąc pod uwagę ograniczenia poprzedniej długości łączącej kilka zadań. | MPM została stworzona w tym samym oku co metoda PERT. Jest ona metodą reprezentacji i optymalizacji zadań projektowych. Można ją uznać za połowę drogi między wykresem Gantta a [[reprezentacja]] PERT. Pozwala ona na nadanie pierwszeństwa dużej ilości zadań biorąc pod uwagę ograniczenia poprzedniej długości łączącej kilka zadań. | ||
Głównym celem stworzenia tej metody było zmniejszenie złożoności wykresu Gantta, biorąc pod uwagę zależności między wieloma zadaniami (pierwszeństwo, dziedziczenie, itd.) oraz ewolucje tych ograniczeń w czasie. | Głównym celem stworzenia tej metody było zmniejszenie złożoności wykresu Gantta, biorąc pod uwagę zależności między wieloma zadaniami (pierwszeństwo, dziedziczenie, itd.) oraz ewolucje tych ograniczeń w czasie. | ||
Największa zaletą metody MPM jest skrócenie czasu potrzebnego do realizacji projektu. Jednak metoda ta uwzględnia tylko planowanie, terminy lub opóźnienia. Nie znajduje zatem zastosowanie w budżecie ani zarządzaniu zasobami. Dzięki precyzyjnemu opisaniu zależności zależności między poszczególnymi zadaniami MPM optymalizuje szybkość procesu równocześnie zapewniając tworząc graficzną reprezentacje w formie sieci. Dzięki temu wszystkie informacje związane z tą samą operacją związane są pod jednym węzłem. Ułatwia to identyfikacje ścieżki krytycznej. | Największa zaletą metody MPM jest skrócenie czasu potrzebnego do realizacji projektu. Jednak metoda ta uwzględnia tylko [[planowanie]], terminy lub opóźnienia. Nie znajduje zatem zastosowanie w budżecie ani zarządzaniu zasobami. Dzięki precyzyjnemu opisaniu zależności zależności między poszczególnymi zadaniami MPM optymalizuje szybkość procesu równocześnie zapewniając tworząc graficzną reprezentacje w formie sieci. Dzięki temu wszystkie [[informacje]] związane z tą samą operacją związane są pod jednym węzłem. Ułatwia to identyfikacje ścieżki krytycznej. | ||
Dzięki łatwej identyfikacji ścieżki krytycznej MPM służy do określania minimalnego czasu wymaganego do przeprowadzenia projektu. Ponadto metoda ta pozwala określić terminy, w których różne zadania związane z projektem mogą lub muszą zapewniać przestrzeganie minimalnego czasu. | Dzięki łatwej identyfikacji ścieżki krytycznej MPM służy do określania minimalnego czasu wymaganego do przeprowadzenia projektu. Ponadto metoda ta pozwala określić terminy, w których różne zadania związane z projektem mogą lub muszą zapewniać przestrzeganie minimalnego czasu. | ||
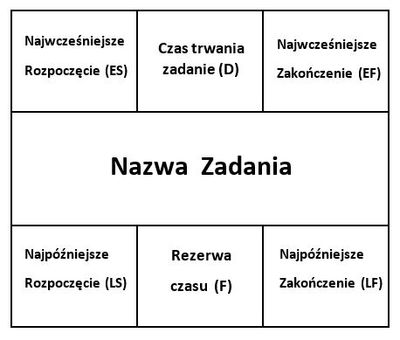
Na Rysunku 1 można zobaczyć jedną składową metody MPM. Przystawia on jedno zadanie, które wchodzi w skład realizowanego projektu. Składa się z sześciu mniejszych okienek - najwcześniejszego (ES) i najpóźniejszego (LS) rozpoczęcia, najwcześniejszego (EF) i najpóźniejszego zakończenia (LF), czasu trwania zadania (D) oraz rezerwy czasu, która nie spowoduje opóźnienia projektu (F). Oprócz tego w centralnej części umieszczona jest nazwa danego zadania. | Na Rysunku 1 można zobaczyć jedną składową metody MPM. Przystawia on jedno [[zadanie]], które wchodzi w skład realizowanego projektu. Składa się z sześciu mniejszych okienek - najwcześniejszego (ES) i najpóźniejszego (LS) rozpoczęcia, najwcześniejszego (EF) i najpóźniejszego zakończenia (LF), czasu trwania zadania (D) oraz rezerwy czasu, która nie spowoduje opóźnienia projektu (F). Oprócz tego w centralnej części umieszczona jest nazwa danego zadania. | ||
== Terminologia == | == Terminologia == | ||
* '''Zadanie''' – jest podstawowym podziałem pracy wymaganym do uzyskania wyniku. Zadanie przekształca się ze stan początkowego do stanu końcowego. Każde zadanie ma czas trwania oraz koszt. | * '''Zadanie''' – jest podstawowym podziałem pracy wymaganym do uzyskania wyniku. Zadanie przekształca się ze stan początkowego do stanu końcowego. Każde zadanie ma czas trwania oraz [[koszt]]. | ||
* '''Zadanie poprzedzające '''- zadanie, które jest tuż przed innym zadaniem. | * '''Zadanie poprzedzające '''- zadanie, które jest tuż przed innym zadaniem. | ||
* '''Zadanie poprzednie '''- zadanie które w odniesieniu do poprzedniego musi być wykonywane wcześniej. | * '''Zadanie poprzednie '''- zadanie które w odniesieniu do poprzedniego musi być wykonywane wcześniej. | ||
* '''Siatka MPM '''– wszystkie etapy i zadania definiujące projekt. Pokazuje związki pomiędzy zadaniami i etapami. | * '''Siatka MPM '''– wszystkie etapy i zadania definiujące [[projekt]]. Pokazuje związki pomiędzy zadaniami i etapami. | ||
* '''Etap '''- kok, początek lb koniec zadania, nie posiada czasu ani kosztów. | * '''Etap '''- kok, początek lb koniec zadania, nie posiada czasu ani kosztów. | ||
* '''Ścieżka krytyczna '''– najdłuższa możliwa ścieżka od początku rozpoczynającego zadania do zakończenia zadania ostatniego. Określa całkowity czas wymagany do realizacji projektu. Wszystkie opóźnienia wzdłuż tej ścieżki opóźniają realizacje projektu. | * '''[[Ścieżka krytyczna]] '''– najdłuższa możliwa ścieżka od początku rozpoczynającego zadania do zakończenia zadania ostatniego. Określa całkowity czas wymagany do realizacji projektu. Wszystkie opóźnienia wzdłuż tej ścieżki opóźniają realizacje projektu. | ||
* '''Zapas '''– dodatkowy dostępny czas lub zasoby potrzebne do wykonania zadania. Pokazuje możliwe opóźnienie jakie może mieć pojedyncze zadanie bez opóźnienia całego procesu <ref>(J. Woźniak, P. Zaskórski, K. Szwarc, Ł. Tomaszewski 2013)</ref> | * '''[[Zapas]] '''– dodatkowy dostępny czas lub [[zasoby]] potrzebne do wykonania zadania. Pokazuje możliwe opóźnienie jakie może mieć pojedyncze zadanie bez opóźnienia całego procesu <ref>(J. Woźniak, P. Zaskórski, K. Szwarc, Ł. Tomaszewski 2013)</ref> | ||
== Wdrożenie metody == | == Wdrożenie metody == | ||
Analiza powstałego grafu pozawala na określenie najwcześniejszego a także najpóźniejszego terminu rozpoczęcia i zakończenia danej czynności. Pozwala ona również wyznaczyć zapas czasu i rezerwy czynności. Jest to długość czasu, o którą można opóźnić realizację danej czynności, nie doprowadzając przy tum do opóźnienia całego procesu. Przez analizę sieci powiązań można określić ścieżkę i czynności krytyczne. Ścieżka krytyczna składa się z dwóch kroków – w przód i w tył. Krok w przód to najpóźniejszy moment, w którym możemy rozpocząć i zakończyć czynność, krok w przód to inaczej najwcześniejszy moment, w którym rozpoczynamy i kończymy czynność. Manewry te muszą być składową analizowanego projektu. Jak w innych metodach sieciowych w skład metody wchodzi graf stworzony z węzłów i krawędzi. Jednak w odróżnieniu od innych metod węzły to czynności a krawędzie (ze strzałkami kierunkowymi) służą tylko do uporządkowania grafu. Pokazują kolejność i zależności pomiędzy czynnościami w konkretnym czasie. Pod i nad krawędziami zapisywane są liczby, które określają one najpóźniejszy i najwcześniejszy moment rozpoczęcia czynności. Wartość najpóźniejsza zapisywana jest ze znakiem ujemnym, natomiast najwcześniejsza ze znakiem dodatnim. <ref>(A. Krakowiak-Bal 2012)</ref> | Analiza powstałego grafu pozawala na określenie najwcześniejszego a także najpóźniejszego terminu rozpoczęcia i zakończenia danej czynności. Pozwala ona również wyznaczyć zapas czasu i rezerwy czynności. Jest to długość czasu, o którą można opóźnić realizację danej czynności, nie doprowadzając przy tum do opóźnienia całego procesu. Przez analizę sieci powiązań można określić ścieżkę i czynności krytyczne. Ścieżka krytyczna składa się z dwóch kroków – w przód i w tył. Krok w przód to najpóźniejszy moment, w którym możemy rozpocząć i zakończyć czynność, krok w przód to inaczej najwcześniejszy moment, w którym rozpoczynamy i kończymy czynność. Manewry te muszą być składową analizowanego projektu. Jak w innych metodach sieciowych w skład metody wchodzi graf stworzony z węzłów i krawędzi. Jednak w odróżnieniu od innych metod węzły to czynności a krawędzie (ze strzałkami kierunkowymi) służą tylko do uporządkowania grafu. Pokazują kolejność i zależności pomiędzy czynnościami w konkretnym czasie. Pod i nad krawędziami zapisywane są liczby, które określają one najpóźniejszy i najwcześniejszy moment rozpoczęcia czynności. [[Wartość]] najpóźniejsza zapisywana jest ze znakiem ujemnym, natomiast najwcześniejsza ze znakiem dodatnim. <ref>(A. Krakowiak-Bal 2012)</ref> | ||
Każdy graf rozpoczyna się od węzła oznaczonego napisem START. Nie oznacza on żadnej czynności. Jego czas jest równy zeru. Od niego liczone są czasy rozpoczęcia i zakończenia czynności. <ref>(A. Woźniak 2010)</ref> | Każdy graf rozpoczyna się od węzła oznaczonego napisem START. Nie oznacza on żadnej czynności. Jego czas jest równy zeru. Od niego liczone są czasy rozpoczęcia i zakończenia czynności. <ref>(A. Woźniak 2010)</ref> | ||
| Linia 54: | Linia 54: | ||
* Krakowiak-Bal A. (2012) ''[http://agro.icm.edu.pl/agro/element/bwmeta1.element.agro-61d76734-e006-48e3-87a3-3440d480e2a5/c/17.pdf. Wykorzystanie metod planowania sieciowego do usprawnienia procesów logistycznych na przykładzie przedsiębiorstwa rolno-spożywczego]'', Polska Akademia Nauk, Kraków | * Krakowiak-Bal A. (2012) ''[http://agro.icm.edu.pl/agro/element/bwmeta1.element.agro-61d76734-e006-48e3-87a3-3440d480e2a5/c/17.pdf. Wykorzystanie metod planowania sieciowego do usprawnienia procesów logistycznych na przykładzie przedsiębiorstwa rolno-spożywczego]'', Polska Akademia Nauk, Kraków | ||
* Pietras P. Szmit M., (2003) ''[http://www.pmpp.pl/download/skrypt1.pdf Zarządzanie projektami wybrane metody i techniki''], Oficyna Księgarsko-Wydawnicza Horyzont, Łódź | * Pietras P. Szmit M., (2003) ''[http://www.pmpp.pl/download/skrypt1.pdf Zarządzanie projektami wybrane metody i techniki''], Oficyna Księgarsko-Wydawnicza Horyzont, Łódź | ||
* Woźniak J. Zaskórski P. Szwarc K. Tomaszewski Ł., (2013) '' Zarządzanie projektami w ujęciu systemowym'', Wojskowa Akademia Techniczna | * Woźniak J. Zaskórski P. Szwarc K. Tomaszewski Ł., (2013) '' [[Zarządzanie]] projektami w ujęciu systemowym'', Wojskowa Akademia Techniczna | ||
* Woźniak A., (2010) ''Grafy i sieci w technikach decyzyjnych, Infrastruktura i Ekologia Terenów Wiejskich'' Kraków, | * Woźniak A., (2010) ''Grafy i sieci w technikach decyzyjnych, [[Infrastruktura]] i [[Ekologia]] Terenów Wiejskich'' Kraków, | ||
[[Kategoria:Zarządzanie projektami]] | [[Kategoria:Zarządzanie projektami]] | ||
{{a|Martyna Sołtys}} | {{a|Martyna Sołtys}} | ||
Wersja z 04:57, 20 maj 2020
| MPM |
|---|
| Polecane artykuły |
Metra Potential Method (MPM) to narzędzie do zarządzania projektami, opracowane w 1958 roku przez francuza Bernarda Roya. Narzędzie to służy do opisywania, organizowania i planowania zadań, które stanowią rozwój projektu. Metoda ta jest podobna do metody PERT. Wierzchołki pokazują zadania, a połączenia przedstawiają ograniczenie pierwszeństwa zadań.
Historia
Bernard Roy był francuskim badacze. Urodził się w 1934 roku. Był bardzo uznanym pionierem w dziedzinie badań operacyjnych we Francji. Obecnie jego badania tworzą jeden z fundamentów naukowych podejść do wspierania decyzji. W 1958 roku opisał metodę MPM opartą na teorii grafów. Pierwotnie metoda ta została zastosowana w fabryce wałów korbowych Mavilor. Wkrótce potem została wykorzystana do budowy nawierzchni linii France. Początkiem lat sześćdziesiątych MPM zostało zaangażowane w rozwój programu samolotów Concorde, a także budowę pierwszych elektrowni jądrowych we Francji. [1]
Koncepcja
MPM została stworzona w tym samym oku co metoda PERT. Jest ona metodą reprezentacji i optymalizacji zadań projektowych. Można ją uznać za połowę drogi między wykresem Gantta a reprezentacja PERT. Pozwala ona na nadanie pierwszeństwa dużej ilości zadań biorąc pod uwagę ograniczenia poprzedniej długości łączącej kilka zadań. Głównym celem stworzenia tej metody było zmniejszenie złożoności wykresu Gantta, biorąc pod uwagę zależności między wieloma zadaniami (pierwszeństwo, dziedziczenie, itd.) oraz ewolucje tych ograniczeń w czasie.
Największa zaletą metody MPM jest skrócenie czasu potrzebnego do realizacji projektu. Jednak metoda ta uwzględnia tylko planowanie, terminy lub opóźnienia. Nie znajduje zatem zastosowanie w budżecie ani zarządzaniu zasobami. Dzięki precyzyjnemu opisaniu zależności zależności między poszczególnymi zadaniami MPM optymalizuje szybkość procesu równocześnie zapewniając tworząc graficzną reprezentacje w formie sieci. Dzięki temu wszystkie informacje związane z tą samą operacją związane są pod jednym węzłem. Ułatwia to identyfikacje ścieżki krytycznej.
Dzięki łatwej identyfikacji ścieżki krytycznej MPM służy do określania minimalnego czasu wymaganego do przeprowadzenia projektu. Ponadto metoda ta pozwala określić terminy, w których różne zadania związane z projektem mogą lub muszą zapewniać przestrzeganie minimalnego czasu.
Na Rysunku 1 można zobaczyć jedną składową metody MPM. Przystawia on jedno zadanie, które wchodzi w skład realizowanego projektu. Składa się z sześciu mniejszych okienek - najwcześniejszego (ES) i najpóźniejszego (LS) rozpoczęcia, najwcześniejszego (EF) i najpóźniejszego zakończenia (LF), czasu trwania zadania (D) oraz rezerwy czasu, która nie spowoduje opóźnienia projektu (F). Oprócz tego w centralnej części umieszczona jest nazwa danego zadania.
Terminologia
- Zadanie – jest podstawowym podziałem pracy wymaganym do uzyskania wyniku. Zadanie przekształca się ze stan początkowego do stanu końcowego. Każde zadanie ma czas trwania oraz koszt.
- Zadanie poprzedzające - zadanie, które jest tuż przed innym zadaniem.
- Zadanie poprzednie - zadanie które w odniesieniu do poprzedniego musi być wykonywane wcześniej.
- Siatka MPM – wszystkie etapy i zadania definiujące projekt. Pokazuje związki pomiędzy zadaniami i etapami.
- Etap - kok, początek lb koniec zadania, nie posiada czasu ani kosztów.
- Ścieżka krytyczna – najdłuższa możliwa ścieżka od początku rozpoczynającego zadania do zakończenia zadania ostatniego. Określa całkowity czas wymagany do realizacji projektu. Wszystkie opóźnienia wzdłuż tej ścieżki opóźniają realizacje projektu.
- Zapas – dodatkowy dostępny czas lub zasoby potrzebne do wykonania zadania. Pokazuje możliwe opóźnienie jakie może mieć pojedyncze zadanie bez opóźnienia całego procesu [2]
Wdrożenie metody
Analiza powstałego grafu pozawala na określenie najwcześniejszego a także najpóźniejszego terminu rozpoczęcia i zakończenia danej czynności. Pozwala ona również wyznaczyć zapas czasu i rezerwy czynności. Jest to długość czasu, o którą można opóźnić realizację danej czynności, nie doprowadzając przy tum do opóźnienia całego procesu. Przez analizę sieci powiązań można określić ścieżkę i czynności krytyczne. Ścieżka krytyczna składa się z dwóch kroków – w przód i w tył. Krok w przód to najpóźniejszy moment, w którym możemy rozpocząć i zakończyć czynność, krok w przód to inaczej najwcześniejszy moment, w którym rozpoczynamy i kończymy czynność. Manewry te muszą być składową analizowanego projektu. Jak w innych metodach sieciowych w skład metody wchodzi graf stworzony z węzłów i krawędzi. Jednak w odróżnieniu od innych metod węzły to czynności a krawędzie (ze strzałkami kierunkowymi) służą tylko do uporządkowania grafu. Pokazują kolejność i zależności pomiędzy czynnościami w konkretnym czasie. Pod i nad krawędziami zapisywane są liczby, które określają one najpóźniejszy i najwcześniejszy moment rozpoczęcia czynności. Wartość najpóźniejsza zapisywana jest ze znakiem ujemnym, natomiast najwcześniejsza ze znakiem dodatnim. [3]
Każdy graf rozpoczyna się od węzła oznaczonego napisem START. Nie oznacza on żadnej czynności. Jego czas jest równy zeru. Od niego liczone są czasy rozpoczęcia i zakończenia czynności. [4]
Przypisy
Bibliografia
- Halicki M. (2010) Zarządzanie projektami w procesie ewolucji struktur organizacyjnych przedsiębiorstw Uniwersytet Ekonomiczny w Poznaniu, Poznań
- Krakowiak-Bal A. (2012) Wykorzystanie metod planowania sieciowego do usprawnienia procesów logistycznych na przykładzie przedsiębiorstwa rolno-spożywczego, Polska Akademia Nauk, Kraków
- Pietras P. Szmit M., (2003) Zarządzanie projektami wybrane metody i techniki, Oficyna Księgarsko-Wydawnicza Horyzont, Łódź
- Woźniak J. Zaskórski P. Szwarc K. Tomaszewski Ł., (2013) Zarządzanie projektami w ujęciu systemowym, Wojskowa Akademia Techniczna
- Woźniak A., (2010) Grafy i sieci w technikach decyzyjnych, Infrastruktura i Ekologia Terenów Wiejskich Kraków,
Autor: Martyna Sołtys