Drzewo zdarzeń: Różnice pomiędzy wersjami

Z Encyklopedia Zarządzania
Nie podano opisu zmian
m (cleanup bibliografii i rotten links)
 
(Nie pokazano 52 wersji utworzonych przez 3 użytkowników)
Linia 1: Linia 1:
'''Drzewo zdarzeń''' to indukcyjny diagram pozwalający na analizę potencjalnych '''skutków''' danego wydarzenia zawierający chronologiczną serię zdarzeń, będących następstwem wydarzenia inicjującego<ref name="ntnu">M. Rausand 2021</ref>. Zdarzeniami mogą być konkretne działania lub stany natury. Obrazuje '''progresję zdarzeń''' od inicjującego do wyniku końcowego, jego głównym celem jest [[identyfikacja]] wszystkich możliwych scenariuszy wynikających z pierwszego zdarzenia<ref name="ntnu" />.


Owe narzędzie analityczne jest podstawą do zastosowania metody ''Event Tree Analysis'' ETA czyli '''Analizy Drzewa Zdarzeń'''. Uznawana za jedną z '''metod ilościowych''' oceny ryzyka, pozwala na wyznaczenie prawdopodobieństwa wystąpienia poszczególnych skutków danego zdarzenia<ref name="psk">W. Mąka 2006</ref>. Jej pochodzenie nie zostało jednoznacznie ustalone, jednak po raz pierwszy użyto jej oficjalnie w raporcie NRC (''Nuclear Regulatory Commision'') czyli amerykańskiego Urzędu Dozoru Jądrowego ''The Reactor Safety Study''<ref>N.C. Rasmussen 1975</ref>.


'''Drzewo zdarzeń''' to indukcyjny diagram pozwalający na analizę potencjalnych '''skutków''' danego wydarzenia zawierający chronologiczną serię zdarzeń, będących następstwem wydarzenia inicjującego <ref>[https://books.google.pl/books?id=x4Ft7H_2Ik0C&pg=PA69&redir_esc=y#v=onepage&q&f=false J. X. Wang, M. L. Roush 2000]</ref>. Zdarzeniami mogą być konkretne działania lub stany natury. Obrazuje '''progresję zdarzeń''' od inicjującego do wyniku końcowego przy pomocy algebry Boole'a, ich konsekwencje, a także uwzględnia zjawiska mające szczególne znaczenie dla stanu obiektu (systemu) <ref>[https://en.wikipedia.org/wiki/Event_tree Event Tree 2021]</ref>.
Sama struktura drzewa daje szansę spojrzeć na [[ryzyko]] związane z danym wydarzeniem również z perspektywy analizy jakościowej, a więc na zorientowanie się w sytuacji, która została poddana ocenie<ref name="psk" />.


Owe narzędzie analityczne jest podstawą do zastosowania metody ''Event Tree Analysis'' ETA czyli '''Analizy Drzewa Zdarzeń'''. Uznawana za jedną z metod oceny '''ryzyka ilościowego''', pozwala na wyznaczenie prawdopodobieństwa wystąpienia poszczególnych skutków danego zdarzenia<ref name="psk">[https://edu.pjwstk.edu.pl/wyklady/psk/scb/index14.html W. Mąka 2006]</ref>. Jej pochodzenie nie zostało jednoznacznie ustalone, jednak po raz pierwszy użyto jej oficjalnie w raporcie NRC (''Nuclear Regulatory Commision'') czyli amerykańskiego Urzędu Dozoru Jądrowego „''The Reactor Safety Study''” (NUREG-75/014, 1975) <ref name="risk">[https://books.google.pl/books?hl=en&lr=&id=9EHeLmbUVh8C&oi=fnd&pg=PT12&ots=ZYyphoW4M6&sig=BEZAk58dstuNHJpRz5z5nTFBpSI&redir_esc=y#v=onepage&q=event%20tree&f=false M. Rausand 2011]</ref>.
==TL;DR==
Drzewo zdarzeń to narzędzie analizy potencjalnych skutków danego wydarzenia. Metoda analizy drzewa zdarzeń pozwala na ocenę ilościową ryzyka poprzez wyznaczenie prawdopodobieństwa wystąpienia skutków. Proces tworzenia drzewa zdarzeń obejmuje określenie zdarzenia inicjującego, identyfikację kolejnych zdarzeń, konstrukcję drzewa, wyznaczenie prawdopodobieństwa zdarzeń i podsumowanie wyników. Metoda ta ma wiele zalet, takich jak prostota tworzenia, matematyczne wyznaczanie prawdopodobieństwa i zastosowanie w ocenie ryzyka. Jednak ma też wady, takie jak brak standardu graficznego przedstawienia i subiektywny wybór zdarzeń. Drzewo porażek może być uzupełnieniem drzewa zdarzeń i służy do analizy przyczyn i prawdopodobieństwa porażki. Istnieje oprogramowanie wspierające tworzenie diagramu drzewa zdarzeń i obliczenia probabilistyczne.


Sama struktura drzewa daje szansę spojrzeć na ryzyko związane z danym wydarzeniem również z perspektywy analizy jakościowej, a więc na zorientowanie się w sytuacji, która została poddana ocenie<ref name="psk" />.
==Etapy tworzenia i analizy drzewa==
Nie istnieje żaden uniwersalny standard pozwalający na konstrukcję drzewa zdarzeń, jednak za Marvinem Rausand'em można przytoczyć poniższy schemat:
# Zdefiniowanie zdarzenia inicjującego.
# Identyfikacja barier i zdarzeń następujących.
# Budowa drzewa zdarzeń.
# Opis wydarzeń końcowych.
# Wyznaczenie prawdopodobieństwa lub częstotliwości zdarzeń pośrednich.
# Ustalenie prawdopodobieństwa lub częstotliwości zdarzeń końcowych.
# Podsumowanie<ref name="ntnu" />
Probabilistyczna [[ocena]] ryzyka rozpoczyna się '''zdefiniowaniem systemu''', którego analiza dotyczy, a następnie inicjujących wydarzeń, które zmieniają stan czy konfigurację owego środowiska. Należy uświadomić sobie [[cele]] i ograniczenia, zgromadzić istotne [[dane]], a w końcu wybrać '''jedno [[zdarzenie]]''' od którego rozpocznie się diagram. Jeśli pojawiło się więcej niż jedno niezależne zdarzenie, należy zbudować kilka osobnych diagramów, albowiem drzewo powinno zaczynać się od jednego konkretnego punktu wyjścia.


== Etapy tworzenia i analizy drzewa<ref name="risk" />==
<google>n</google>
# Planowanie i przygotowanie
# Zdefiniowanie zdarzenia inicjującego
# Identyfikacja barier i zdarzeń następujących
# Budowa drzewa zdarzeń
# Opis wydarzeń końcowych
# Ustalenie prawdopodobieństwa lub częstotliwości zdarzeń końcowych
# Podsumowanie


Probabilistyczna ocena ryzyka rozpoczyna się '''zdefiniowaniem systemu''', którego analiza dotyczy, a następnie inicjujących wydarzeń, które zmieniają stan czy konfigurację owego środowiska. Należy uświadomić sobie cele i ograniczenia, zgromadzić istotne dane, a w końcu wybrać '''jedno zdarzenie''' od którego rozpoczniemy. Jeśli pojawiło się więcej niż jedno niezależne zdarzenie, należy zbudować kilka osobnych diagramów, albowiem drzewo powinno zaczynać się od jednego konkretnego punktu wyjścia. 
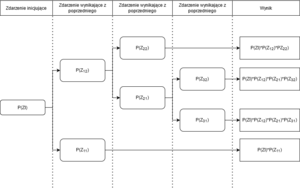
[[Plik:ETA2(1).png|300px|right|thumb|Rys. 1 Przykład struktury Drzewa Zdarzeń]]


'''Zdarzenie inicjujące''' musi zostać starannie określone i pozostawać w określonych ramach (odpowiadając na przykład na pytanie co, gdzie, kiedy?). Dzieje się to w kroku drugim gdzie niejako kategoryzuje się zdarzenie.  
'''Zdarzenie inicjujące''' musi zostać starannie określone i pozostawać w mierzalnych ramach (odpowiadając na przykład na pytanie co, gdzie, kiedy?)<ref name="ntnu" />. W razie wątpliwości można posłużyć się zasadą wyboru pierwszej znaczącej dewiacji (ang. ''first significant deviation'')<ref name="ntnu" />.


W kroku trzecim określa się bariery, szanse, kluczowe wydarzenia mające znaczenie dla danego systemu, a związane z wydarzeniem z punktu drugiego.
W kroku następnym określa się bariery, [[szanse]], kluczowe wydarzenia mające znaczenie dla danego systemu, a związane z wydarzeniem początkowym. Zaczyna się próbować odpowiadać na pytanie "co jeśli?" wydarzenie inicjujące dojdzie do skutku.


Dalej konstruuje się samo drzewo. Pierwsze zdarzenie, określone w kroku drugim, rozpoczyna cały proces, na przykład rozpalenie zapałki czy włączenie lampy. Każde kolejne jest jego konsekwencją ujętą '''zazwyczaj binarnie''', to znaczy dostępne są dwa warianty skutków danego wydarzenia: tak lub nie albo inaczej sukces lub porażka. Sekwencja ta jest powtarzana, aż osiągnięty zostanie '''stan końcowy''' (kontynuując wspomniane dwa przykłady: drzewo nie dostarcza owoców czy raport nie został dostarczony na czas). Budując kolejne etapy struktury należy zadawać sobie pytania:
Dalej konstruuje się samo drzewo. Pierwsze zdarzenie, określone na początku, rozpoczyna cały [[proces]], na przykład rozpalenie zapałki czy włączenie lampy. Każde kolejne jest jego konsekwencją ujętą '''zazwyczaj binarnie''', to znaczy dostępne są dwa [[warianty]] skutków danego wydarzenia: [[sukces]] lub porażka, wydarzenie niespodziewane lub standardowa operacja systemu<ref name="clem" />. Sekwencja ta jest powtarzana, aż osiągnięty zostanie '''stan końcowy''' (kontynuując wspomniane dwa przykłady: drzewo nie dostarcza owoców czy raport nie został dostarczony na czas).
* "Czy system nadal działa w tej części gałęzi po wystąpieniu poszczególnych zdarzeń poprzedzających?
* Czy sukces lub porażka systemu wpływa na wydarzenie końcowe?
* Czy zachowanie danego systemu w tym momencie mogłaby poskutkować zastosowaniem jakiegoś mechanizmu bezpieczeństwa?
* Czy operacyjność danego systemu wpływa na działanie innych systemów?"<ref name="risk" />


Istnieją różne formy wizualnego przedstawienia drzewa zdarzeń. Najczęściej spotykanym w literaturze sposobem jest umieszczenie zdarzenia inicjującego z '''lewej''' strony, zdarzenia następujące rozgałęziają się w prawo. Dodatkowo używając systemu '''binarnego opcja porażki powinna znaleźć się niżej, a sukcesu wyżej'''. Dzięki temu wydarzenia wynikowe powinny same uszeregować się w kolejności od całkowitej porażki (najgorszego możliwego scenariusza) na dole, do wyniku składającego się z samych sukcesów na szczycie. W środku znajdą się wyniki zawierające ciągi zdarzeń zawierające zarówno porażki, jak i zwycięstwa. Takie ujęcie ułatwia końcową analizę.
Istnieją różne formy wizualnego przedstawienia drzewa zdarzeń. Najczęściej spotykanym w literaturze sposobem jest umieszczenie zdarzenia inicjującego z '''lewej''' strony, zdarzenia następujące rozgałęziają się w [[prawo]]<ref name="marine">A. Raiyan, S. Dasa, M. Rafiqul Islam 2017</ref>. Dodatkowo używając systemu '''binarnego [[opcja]] porażki powinna znaleźć się niżej, a sukcesu wyżej'''. Dzięki temu wydarzenia wynikowe powinny same uszeregować się w kolejności od całkowitej porażki (najgorszego możliwego scenariusza) na dole, do wyniku składającego się z samych sukcesów na szczycie. W środku znajdą się wyniki zawierające ciągi zdarzeń z zarówno porażkami, jak i zwycięstwami. Takie ujęcie ułatwia końcową analizę.


Skąd wiadomo, co powinno być '''wydarzeniem końcowym'''? Poddając analizie wypadek samochodowy wydarzeniem końcowym będzie uraz kierowcy czy raczej okoliczności udzielenia mu pierwszej pomocy? Na te pytania nie ma jednej właściwej odpowiedzi, wszystko zależy od założeń i zakresu ustalonego na początku środowiska (wiąże się to z zakresem analizy ryzyka)<ref name="risk" />.
Skąd wiadomo, co powinno być '''wydarzeniem końcowym'''? Poddając analizie zapalenie zapałki należy zakończyć na spaleniu drzewa, zaprzestaniu przez drzewo dostarczania owoców czy niedotrzymaniu przez firmę terminów dostaw soków? Na te pytania nie ma jednej właściwej odpowiedzi, wszystko zależy od założeń i zakresu ustalonego na początku systemu.


Przedostatnim etapem jest '''określenie prawdopodobieństwa wystąpienia wydarzenia końcowego'''. Każda gałąź musi mieć swoje określone prawdopodobieństwo. Istnieje wiele sposobów na jego wyznaczenie. Może zostać zdefiniowane na podstawie testów, obliczeń, ogólnodostępnych statystyk czy wynikać z drzewa błędów. Jeśli warianty mają formę binarną, a prawdopodobieństwo porażki zostanie obliczone za pomocą analizy drzewa porażek FTA (ang. ''Fault Tree Analysis''), szanse na sukces mogą zostać wyznaczone na podstawie poniższej zależności <ref name=hazard>Clifton A., Ericson II 2005</ref>:
Przedostatnim etapem jest '''określenie prawdopodobieństwa wystąpienia wydarzenia końcowego'''. Każda gałąź musi mieć swoje określone [[prawdopodobieństwo]]. Istnieje wiele sposobów na jego wyznaczenie. Może zostać zdefiniowane na podstawie testów, obliczeń, ogólnodostępnych statystyk czy wynikać z drzewa błędów<ref name="psk" />. Jeśli warianty mają formę binarną, a prawdopodobieństwo porażki zostanie obliczone za pomocą analizy drzewa porażek FTA (ang. ''Fault Tree Analysis''), szanse na sukces mogą zostać wyznaczone na podstawie poniższej zależności<ref>J.D. Andrews, S.J. Dunnett 2000, s. 230-238</ref>:


1 = p(s)+p(f)
<math> P_S = 1 - P_F</math>


Przykład:
Przykład:


p(f) = 0,3 -> p(s) = 1-0,3 = 0,7
<math> P_F = 0,3 </math>


Znając prawdopodobieństwo wystąpienia każdego zdarzenia zawartego w diagramie, wyznacza się szansę na wystąpienie zdarzeń końcowych. Jest ona '''iloczynem''' poszczególnych wartości na ścieżce do niego prowadzącej z prawdopodobieństwem zdarzenia inicjującego włącznie <ref name="wiki">[https://en.wikipedia.org/wiki/Event_tree_analysis, Event Tree Analysis 2021]</ref>.
<math> P_S = 1-0,3 = 0,7</math>


P(W) = P(Z<sub>I</sub>) * P(Z<sub>Z1</sub>) * … * P(Z<sub>n</sub>)
Znając prawdopodobieństwo wystąpienia każdego zdarzenia zawartego w diagramie, wyznacza się szansę na wystąpienie zdarzeń końcowych. Jest ona często '''iloczynem''' poszczególnych wartości na ścieżce do niego prowadzącej z prawdopodobieństwem zdarzenia inicjującego włącznie <ref name="marine" />:


Ostatnim etapem jest podsumowanie znalezionych wariantów i stworzenie uporządkowanego '''raportu'''.
<math> P(W) = P(Z_I)*P(Z_Z1)* ... *P(Z_n)</math>


Ostatnim etapem jest podsumowanie znalezionych wariantów i prezentacja ich w postaci uporządkowanego '''raportu'''<ref name="ntnu" />.


== Zalety metody ==
==Zalety metody==
Główne zalety zastosowania drzewa zdarzeń i jego analizy:
* Prostota tworzenia.
* Matematyczne wyznaczenie prawdopodobieństwa wystąpienia zdarzeń końcowych.
* Zastosowanie w ocenie ilościowej, ale i jakościowej<ref name="psk" />.
* Pozwala określić punkty newralgiczne, luki w systemie czy jego zabezpieczeniach, dzięki czemu można je zaadresować<ref name="clem">P.L. Clemens, R.J. Simmons 1998, VII-3,VII-14, IX-3,IX-7</ref>.
* Tworzenie modeli skomplikowanych systemów w przejrzysty sposób.
* Brak [[potrzeby]] przewidywania zdarzeń końcowych, wynikają one z poprzednich <ref name="clem" />.
* Cały proces może zostać zautomatyzowany za pomocą oprogramowania.


* Łatwość przyswojenia oraz zastosowania<ref name="hazard" />
==Wady metody==
* Modelowanie skomplikowanych systemów w przejrzysty sposób <ref name="hazard" />
Drzewo zdarzeń i jego analiza ma również swoje wady:
* Wyznaczenie prawdopodobieństwa <ref name="hazard" />
* Brak jednoznacznie określonego standardu graficznego przedstawienia<ref name="ntnu" />.
* Pozwala określić punkty newralgiczne, luki w systemie czy jego zabezpieczeniach, dzięki czemu można je zaadresować<ref name="clem">P.L. Clemens, R.J. Simmons 1998</ref>
* Można wyznaczyć ścieżki prowadzące do porażek, ale [[skala]] strat może się różnić na każdej z nich<ref name="clem" />.
* Brak potrzeby przewidywania zdarzeń końcowych, wynikają one z poprzednich  <ref name="clem" />
* W niektórych przypadkach wyznaczenie prawdopodobieństwa zdarzenia pośredniego może być skomplikowane lub niedokładne<ref name="clem" />.
* Cały proces może zostać zautomatyzowany za pomocą oprogramowania  <ref name="hazard" />
* Może zawierać tylko jedno zdarzenie inicjujące na raz<ref name="clem" />.
* Zdarzenia są zazwyczaj subiektywnie wybierane przez tworzącego diagram<ref name="clem" />.


==Drzewo Porażek==
'''Drzewo porażek''' (lub inaczej błędów) może być niejako dopełnieniem obrazu sytuacji opisywanej przez drzewo zdarzeń. Jak wspomniano, może umożliwić obliczenie '''prawdopodobieństwa porażki'''. Jego struktura jest jednak odwrotna, '''inicjatorem jest skutek''', a gałęzie określają zbiory tzw. '''cięć''' i '''ścieżek'''<ref name="clem" />. "Zbiór cięć jest grupą inicjatorów, które sprawią, że główne wydarzenie dojdzie do skutku, zaś jeśli zdarzenia z grupy ścieżek nie dojdą do skutku zagwarantują skutek odwrotny (brak badanego wydarzenia)"<ref name="clem" />. Analiza drzewa porażek służy do przestudiowania '''przyczyn''' danego zdarzenia i prawdopodobieństw ich wystąpienia, kiedy analiza drzewa zdarzeń nakreśla potencjalne '''scenariusze następstw''' tego samego wypadku.


Pozwala na zobrazowanie wszystkich potencjalnych kombinacji wydarzeń prowadzących do badanej sytuacji, identyfikację punktów newralgicznych oraz ich ocenę, znalezienie słabych punktów i przeciwdziałanie im w celu kontroli ryzyka<ref name="clem" />.


== Wady metody ==
Tak jak Drzewo zdarzeń jest narzędziem koniecznym analizie drzewa zdarzeń, tak drzewo porażek jest używane w analizie drzewa porażek.


* Brak jednoznacznie określonego standardu graficznego  <ref name="risk" />
==Oprogramowanie wspomagające tworzenie diagramu==
* Nie obsługuje możliwości zatrzymania przed zdarzeniem końcowym lub ominięcia któregoś zdarzenia pośredniego  <ref name="risk" />
W celu ułatwienia i przyspieszenia procesu przygotowania diagramu drzewa zdarzeń oraz wykonania obliczeń probabilistycznych na rynku pojawiło się wiele oprogramowań. Istnieją zarówno licencjonowane, wykorzystywane w przemyśle, jak na licencji wolnej (''[[Open Source]]''), a więc dostępne dla każdego. Przykłady:
* W niektórych przypadkach wyznaczenie prawdopodobieństwa zdarzenia pośredniego może być skomplikowane lub niedokładne  <ref name="clem" />
* RiskSpectrum PSA - używane w przemyśle jądrowym
* ALD Services


== Drzewo Porażek ==
{{infobox5|list1={{i5link|a=[[GERT]]}} &mdash; {{i5link|a=[[MOCRA]]}} &mdash; {{i5link|a=[[Diagram procesu]]}} &mdash; {{i5link|a=[[PERT]]}} &mdash; {{i5link|a=[[Zarządzanie projektem zagrożonym]]}} &mdash; {{i5link|a=[[Drzewo decyzyjne]]}} &mdash; {{i5link|a=[[Drzewo celów]]}} &mdash; {{i5link|a=[[7 narzędzi TQC]]}} &mdash; {{i5link|a=[[Zarządzanie ryzykiem]]}} }}


'''Drzewo porażek''' (lub inaczej błędów) może być niejako dopełnieniem obrazu sytuacji opisywanej przez drzewo zdarzeń. Jak wspomniano, może umożliwić obliczenie prawdopodobieństwa porażki. Jego struktura jest jednak odwrotna. W tym przypadku rozpoczyna się od określenia '''skutku''', a gałęzie do niego prowadzące są potencjalnymi przyczynami, które mogły doprowadzić do danego zdarzenia <ref name="fault">[https://en.wikipedia.org/wiki/Fault_tree_analysis Fault Tree Analysis 2021] </ref>. Analiza drzewa porażek służy do przestudiowania '''przyczyn''' danego zdarzenia, kiedy analiza drzewa zdarzeń nakreśla potencjalne '''scenariusze następstw''' tego samego wypadku.
==Przypisy==
 
Pozwala na zobrazowanie potencjalnych wariantów sytuacji, dzięki czemu można się na nie przygotować wprowadzając środki zaradcze i zminimalizować prawdopodobieństwo osiągnięcia niepożądanego skutku <ref name="fault" />.
 
Tak jak Drzewo zdarzeń jest narzędziem koniecznym analizie drzewa zdarzeń, tak drzewo porażek jest używane w analizie drzewa porażek.
 
== Oprogramowanie ==
 
W celu ułatwienia i przyspieszenia procesu przygotowania diagramu drzewa zdarzeń oraz wykonania obliczeń probabilistycznych na rynku pojawiło się wiele oprogramowań. Istnieją zarówno licencjonowane, wykorzystywane w przemyśle, jak na licencji wolnej (''Open Source''), a więc dostępne dla każdego. Przykłady:
*  RiskSpectrum PSA – używane w przemyśle jądrowym
*  ALD Services
 
 
== Przypisy ==
<references />
<references />


== Bibliografia ==
==Bibliografia==
 
<noautolinks>
Clifton A., Ericson II, "''Hazard Analysis Techniques for System Safety''" John Wiley & Sons, Inc. 2005
* Andrews D., Dunnet S. (2000), ''Event-tree analysis using binary decision diagrams'', IEEE Transactions on Reliability
 
* Clemens P., Simmons R. (1998), ''[https://www.cdc.gov/niosh/docs/96-37768/pdfs/96-37768.pdf System Safety and Risk Management: NIOSH Instructional Module]'', National Institute for Occupational Safety and Health
Clemens P.L., Simmons R.J., "''System Safety and Risk Management: NIOSH Instructional Module''" NIOSH 1998
* Ferdous R., Khan F., Sadiq R., Amyotte P., Veitch B. (2009), ''Handling data uncertainties in event tree analysis'', Process Safety and Environmental Protection
 
* Mąka W. (2006), ''[https://edu.pjwstk.edu.pl/wyklady/psk/scb/index14.html Projektowanie Sieci Komputerowych: Analiza Ryzyka]'', wykład
[https://en.wikipedia.org/wiki/Event_tree Event tree] Wikipedia 2021
* Raiyan A., Dasa S., Rafiqul I. (2017), ''Event Tree Analysis of Marine Accidents in Bangladesh'', Procedia Engineering
 
* Rasmussen N. (1975), ''Reactor Safety Study: An assessment of accident risks in US Commercial Nuclear Power Plants'', Nuclear Regulatory commission
[https://en.wikipedia.org/wiki/Event_tree_analysis Event tree analysis] Wikipedia 2021
* Rausand M. (2021), ''[https://www.ntnu.edu/documents/624876/1277590549/chapt03-eta.pdf/6f3e1b19-4824-4812-adc8-9762d2201c22 Event Tree Analysis]'', NTNU
 
</noautolinks>
[https://en.wikipedia.org/wiki/Fault_tree_analysis Fault tree analysis] Wikipedia 2021
 
Mąka W., "''Projektowanie Sieci Komputerowych: Analiza Ryzyka''" PJWSTK 2006


Rausand M., "''Risk Assessment: Theory, Methods, and Applications''",John Wiley & Sons, Inc. 2011
{{a|K T}}
[[Kategoria:Zarządzanie ryzykiem]]


Wang J.X., Roush M. L. "''What Every Engineer Should Know About Risk Engineering and Management''" Marcel Dekker Inc. 2000
{{#metamaster:description|Drzewo zdarzeń to diagram analizujący skutki wydarzenia. Dowiedz się więcej na stronie.}}

Aktualna wersja na dzień 23:27, 14 sty 2024

Drzewo zdarzeń to indukcyjny diagram pozwalający na analizę potencjalnych skutków danego wydarzenia zawierający chronologiczną serię zdarzeń, będących następstwem wydarzenia inicjującego[1]. Zdarzeniami mogą być konkretne działania lub stany natury. Obrazuje progresję zdarzeń od inicjującego do wyniku końcowego, jego głównym celem jest identyfikacja wszystkich możliwych scenariuszy wynikających z pierwszego zdarzenia[1].

Owe narzędzie analityczne jest podstawą do zastosowania metody Event Tree Analysis ETA czyli Analizy Drzewa Zdarzeń. Uznawana za jedną z metod ilościowych oceny ryzyka, pozwala na wyznaczenie prawdopodobieństwa wystąpienia poszczególnych skutków danego zdarzenia[2]. Jej pochodzenie nie zostało jednoznacznie ustalone, jednak po raz pierwszy użyto jej oficjalnie w raporcie NRC (Nuclear Regulatory Commision) czyli amerykańskiego Urzędu Dozoru Jądrowego The Reactor Safety Study[3].

Sama struktura drzewa daje szansę spojrzeć na ryzyko związane z danym wydarzeniem również z perspektywy analizy jakościowej, a więc na zorientowanie się w sytuacji, która została poddana ocenie[2].

TL;DR

Drzewo zdarzeń to narzędzie analizy potencjalnych skutków danego wydarzenia. Metoda analizy drzewa zdarzeń pozwala na ocenę ilościową ryzyka poprzez wyznaczenie prawdopodobieństwa wystąpienia skutków. Proces tworzenia drzewa zdarzeń obejmuje określenie zdarzenia inicjującego, identyfikację kolejnych zdarzeń, konstrukcję drzewa, wyznaczenie prawdopodobieństwa zdarzeń i podsumowanie wyników. Metoda ta ma wiele zalet, takich jak prostota tworzenia, matematyczne wyznaczanie prawdopodobieństwa i zastosowanie w ocenie ryzyka. Jednak ma też wady, takie jak brak standardu graficznego przedstawienia i subiektywny wybór zdarzeń. Drzewo porażek może być uzupełnieniem drzewa zdarzeń i służy do analizy przyczyn i prawdopodobieństwa porażki. Istnieje oprogramowanie wspierające tworzenie diagramu drzewa zdarzeń i obliczenia probabilistyczne.

Etapy tworzenia i analizy drzewa

Nie istnieje żaden uniwersalny standard pozwalający na konstrukcję drzewa zdarzeń, jednak za Marvinem Rausand'em można przytoczyć poniższy schemat:

  1. Zdefiniowanie zdarzenia inicjującego.
  2. Identyfikacja barier i zdarzeń następujących.
  3. Budowa drzewa zdarzeń.
  4. Opis wydarzeń końcowych.
  5. Wyznaczenie prawdopodobieństwa lub częstotliwości zdarzeń pośrednich.
  6. Ustalenie prawdopodobieństwa lub częstotliwości zdarzeń końcowych.
  7. Podsumowanie[1]

Probabilistyczna ocena ryzyka rozpoczyna się zdefiniowaniem systemu, którego analiza dotyczy, a następnie inicjujących wydarzeń, które zmieniają stan czy konfigurację owego środowiska. Należy uświadomić sobie cele i ograniczenia, zgromadzić istotne dane, a w końcu wybrać jedno zdarzenie od którego rozpocznie się diagram. Jeśli pojawiło się więcej niż jedno niezależne zdarzenie, należy zbudować kilka osobnych diagramów, albowiem drzewo powinno zaczynać się od jednego konkretnego punktu wyjścia.

Rys. 1 Przykład struktury Drzewa Zdarzeń

Zdarzenie inicjujące musi zostać starannie określone i pozostawać w mierzalnych ramach (odpowiadając na przykład na pytanie co, gdzie, kiedy?)[1]. W razie wątpliwości można posłużyć się zasadą wyboru pierwszej znaczącej dewiacji (ang. first significant deviation)[1].

W kroku następnym określa się bariery, szanse, kluczowe wydarzenia mające znaczenie dla danego systemu, a związane z wydarzeniem początkowym. Zaczyna się próbować odpowiadać na pytanie "co jeśli?" wydarzenie inicjujące dojdzie do skutku.

Dalej konstruuje się samo drzewo. Pierwsze zdarzenie, określone na początku, rozpoczyna cały proces, na przykład rozpalenie zapałki czy włączenie lampy. Każde kolejne jest jego konsekwencją ujętą zazwyczaj binarnie, to znaczy dostępne są dwa warianty skutków danego wydarzenia: sukces lub porażka, wydarzenie niespodziewane lub standardowa operacja systemu[4]. Sekwencja ta jest powtarzana, aż osiągnięty zostanie stan końcowy (kontynuując wspomniane dwa przykłady: drzewo nie dostarcza owoców czy raport nie został dostarczony na czas).

Istnieją różne formy wizualnego przedstawienia drzewa zdarzeń. Najczęściej spotykanym w literaturze sposobem jest umieszczenie zdarzenia inicjującego z lewej strony, zdarzenia następujące rozgałęziają się w prawo[5]. Dodatkowo używając systemu binarnego opcja porażki powinna znaleźć się niżej, a sukcesu wyżej. Dzięki temu wydarzenia wynikowe powinny same uszeregować się w kolejności od całkowitej porażki (najgorszego możliwego scenariusza) na dole, do wyniku składającego się z samych sukcesów na szczycie. W środku znajdą się wyniki zawierające ciągi zdarzeń z zarówno porażkami, jak i zwycięstwami. Takie ujęcie ułatwia końcową analizę.

Skąd wiadomo, co powinno być wydarzeniem końcowym? Poddając analizie zapalenie zapałki należy zakończyć na spaleniu drzewa, zaprzestaniu przez drzewo dostarczania owoców czy niedotrzymaniu przez firmę terminów dostaw soków? Na te pytania nie ma jednej właściwej odpowiedzi, wszystko zależy od założeń i zakresu ustalonego na początku systemu.

Przedostatnim etapem jest określenie prawdopodobieństwa wystąpienia wydarzenia końcowego. Każda gałąź musi mieć swoje określone prawdopodobieństwo. Istnieje wiele sposobów na jego wyznaczenie. Może zostać zdefiniowane na podstawie testów, obliczeń, ogólnodostępnych statystyk czy wynikać z drzewa błędów[2]. Jeśli warianty mają formę binarną, a prawdopodobieństwo porażki zostanie obliczone za pomocą analizy drzewa porażek FTA (ang. Fault Tree Analysis), szanse na sukces mogą zostać wyznaczone na podstawie poniższej zależności[6]:

Przykład:

Znając prawdopodobieństwo wystąpienia każdego zdarzenia zawartego w diagramie, wyznacza się szansę na wystąpienie zdarzeń końcowych. Jest ona często iloczynem poszczególnych wartości na ścieżce do niego prowadzącej z prawdopodobieństwem zdarzenia inicjującego włącznie [5]:

Ostatnim etapem jest podsumowanie znalezionych wariantów i prezentacja ich w postaci uporządkowanego raportu[1].

Zalety metody

Główne zalety zastosowania drzewa zdarzeń i jego analizy:

  • Prostota tworzenia.
  • Matematyczne wyznaczenie prawdopodobieństwa wystąpienia zdarzeń końcowych.
  • Zastosowanie w ocenie ilościowej, ale i jakościowej[2].
  • Pozwala określić punkty newralgiczne, luki w systemie czy jego zabezpieczeniach, dzięki czemu można je zaadresować[4].
  • Tworzenie modeli skomplikowanych systemów w przejrzysty sposób.
  • Brak potrzeby przewidywania zdarzeń końcowych, wynikają one z poprzednich [4].
  • Cały proces może zostać zautomatyzowany za pomocą oprogramowania.

Wady metody

Drzewo zdarzeń i jego analiza ma również swoje wady:

  • Brak jednoznacznie określonego standardu graficznego przedstawienia[1].
  • Można wyznaczyć ścieżki prowadzące do porażek, ale skala strat może się różnić na każdej z nich[4].
  • W niektórych przypadkach wyznaczenie prawdopodobieństwa zdarzenia pośredniego może być skomplikowane lub niedokładne[4].
  • Może zawierać tylko jedno zdarzenie inicjujące na raz[4].
  • Zdarzenia są zazwyczaj subiektywnie wybierane przez tworzącego diagram[4].

Drzewo Porażek

Drzewo porażek (lub inaczej błędów) może być niejako dopełnieniem obrazu sytuacji opisywanej przez drzewo zdarzeń. Jak wspomniano, może umożliwić obliczenie prawdopodobieństwa porażki. Jego struktura jest jednak odwrotna, inicjatorem jest skutek, a gałęzie określają zbiory tzw. cięć i ścieżek[4]. "Zbiór cięć jest grupą inicjatorów, które sprawią, że główne wydarzenie dojdzie do skutku, zaś jeśli zdarzenia z grupy ścieżek nie dojdą do skutku zagwarantują skutek odwrotny (brak badanego wydarzenia)"[4]. Analiza drzewa porażek służy do przestudiowania przyczyn danego zdarzenia i prawdopodobieństw ich wystąpienia, kiedy analiza drzewa zdarzeń nakreśla potencjalne scenariusze następstw tego samego wypadku.

Pozwala na zobrazowanie wszystkich potencjalnych kombinacji wydarzeń prowadzących do badanej sytuacji, identyfikację punktów newralgicznych oraz ich ocenę, znalezienie słabych punktów i przeciwdziałanie im w celu kontroli ryzyka[4].

Tak jak Drzewo zdarzeń jest narzędziem koniecznym analizie drzewa zdarzeń, tak drzewo porażek jest używane w analizie drzewa porażek.

Oprogramowanie wspomagające tworzenie diagramu

W celu ułatwienia i przyspieszenia procesu przygotowania diagramu drzewa zdarzeń oraz wykonania obliczeń probabilistycznych na rynku pojawiło się wiele oprogramowań. Istnieją zarówno licencjonowane, wykorzystywane w przemyśle, jak na licencji wolnej (Open Source), a więc dostępne dla każdego. Przykłady:

  • RiskSpectrum PSA - używane w przemyśle jądrowym
  • ALD Services


Drzewo zdarzeń — artykuły polecane
GERT — MOCRA — Diagram procesu — PERT — Zarządzanie projektem zagrożonym — Drzewo decyzyjne — Drzewo celów — 7 narzędzi TQC — Zarządzanie ryzykiem

Przypisy

  1. ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 M. Rausand 2021
  2. ↑ 2,0 2,1 2,2 2,3 W. Mąka 2006
  3. ↑ N.C. Rasmussen 1975
  4. ↑ 4,0 4,1 4,2 4,3 4,4 4,5 4,6 4,7 4,8 4,9 P.L. Clemens, R.J. Simmons 1998, VII-3,VII-14, IX-3,IX-7
  5. ↑ 5,0 5,1 A. Raiyan, S. Dasa, M. Rafiqul Islam 2017
  6. ↑ J.D. Andrews, S.J. Dunnett 2000, s. 230-238

Bibliografia

  • Andrews D., Dunnet S. (2000), Event-tree analysis using binary decision diagrams, IEEE Transactions on Reliability
  • Clemens P., Simmons R. (1998), System Safety and Risk Management: NIOSH Instructional Module, National Institute for Occupational Safety and Health
  • Ferdous R., Khan F., Sadiq R., Amyotte P., Veitch B. (2009), Handling data uncertainties in event tree analysis, Process Safety and Environmental Protection
  • Mąka W. (2006), Projektowanie Sieci Komputerowych: Analiza Ryzyka, wykład
  • Raiyan A., Dasa S., Rafiqul I. (2017), Event Tree Analysis of Marine Accidents in Bangladesh, Procedia Engineering
  • Rasmussen N. (1975), Reactor Safety Study: An assessment of accident risks in US Commercial Nuclear Power Plants, Nuclear Regulatory commission
  • Rausand M. (2021), Event Tree Analysis, NTNU


Autor: K T


Źródło: „https://mfiles.pl/pl/index.php?title=Drzewo_zdarzeń&oldid=213689”