Koszt krańcowy: Różnice pomiędzy wersjami
(LinkTitles.) |
m (cleanup bibliografii i rotten links) |
||
| (Nie pokazano 13 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
'''[[Koszt]] krańcowy''' - inaczej [[koszt marginalny]] (ang. marginal cost, MC) jest to wzrost [[koszt]]ów całkowitych wywołany wzrostem [[produkcja|produkcji]] o jednostkę (Begg, 2003, s. 179). Inaczej mówiąc, jest to koszt wyprodukowania kolejnej (dodatkowej) jednostki [[dobro|dobra]], wykonaniem danej czynności lub świadczeniem [[usługa|usługi]]. | |||
<math>MC=\frac{\Delta TC}{\Delta Q}</math> | |||
Jest to różnica pomiędzy kosztem całkowitym dwóch sąsiednich wielkości produkcji (Beksiak, 2001, s. 70), albo inaczej można powiedzieć jest to [[przyrost]] kosztu (zmiennego bo stały z definicji się nie zmienia) jeśli [[produkcja]] zmieni się o jednostkę. Koszty krańcowe są związane tylko z kosztami zmiennym, ponieważ [[koszty stałe]] nie zmieniają się wraz z rosnącą produkcją. Dlatego właśnie dla rozmiarów oraz zmian kosztu krańcowego - stała cześć sumy kosztów pozostaje bez znaczenia (w przeciwieństwie do kosztu przeciętnego - tam odgrywa dużą rolę). | |||
Przyjmując za podstawę [[koszt przeciętny]], suma kosztów całkowitych będzie iloczynem kosztu przeciętnego oraz ilości wytworzonego produktu. Przyjmując natomiast za podstawę koszt krańcowy - suma kosztów całkowitych będzie suma kolejnych kosztów krańcowych powiększoną o koszty stałe (Dach Z. 2012, s. 172). | |||
==TL;DR== | |||
Koszt krańcowy to wzrost kosztów całkowitych spowodowany wzrostem produkcji o jednostkę. Jest to różnica między kosztem całkowitym dwóch sąsiednich wielkości produkcji. Koszty krańcowe są związane tylko z kosztami zmiennymi. Krzywa kosztu krańcowego najpierw maleje, osiąga minimum, a następnie rośnie. Koszt krańcowy jest mniejszy od przeciętnego kosztu całkowitego, gdy ten maleje, i większy, gdy ten rośnie. Przy wzroście produkcji przeciętny koszt całkowity najpierw maleje, a potem rośnie. | |||
==Geneza== | ==Geneza== | ||
Pojęcie kosztów krańcowych po raz pierwszy pojawiło się w rozważaniach David'a Ricardo (1772-1823) w jego ekonomicznych rozważaniach na temat renty i prawa malejących przychodów (Turgot, 1765r.). | |||
Pojęcie kosztów krańcowych po raz pierwszy pojawiło się w rozważaniach David'a Ricardo (1772-1823) w jego ekonomicznych rozważaniach na temat renty i prawa malejących przychodów (Turgot, 1765r.). | |||
Ricardo analizując rentę z majątku ziemskiego od strony kosztów produkcji zdefiniował [[koszty]] krańcowe. Stwierdził, że [[koszty produkcji]] zboża rosną w miarę, jak ziemia jest uprawiana bardziej intensywnie. Ostatecznie stwierdził, że koszt krańcowy to łączny przyrost kosztu niezbędnego do wytworzenia dodatkowej ilości końcowego produktu. | Ricardo analizując rentę z majątku ziemskiego od strony kosztów produkcji zdefiniował [[koszty]] krańcowe. Stwierdził, że [[koszty produkcji]] zboża rosną w miarę, jak ziemia jest uprawiana bardziej intensywnie. Ostatecznie stwierdził, że koszt krańcowy to łączny przyrost kosztu niezbędnego do wytworzenia dodatkowej ilości końcowego produktu. | ||
Jest to początek znanej i uprawianej do dzisiaj szkoły rachunku marginalnego, której istotą nie są wartości globalne lecz jej przyrosty i warunki ich zmian. | Jest to początek znanej i uprawianej do dzisiaj szkoły rachunku marginalnego, której istotą nie są wartości globalne lecz jej przyrosty i warunki ich zmian. | ||
<google> | <google>n</google> | ||
==Prawo malejących przychodów== | ==Prawo malejących przychodów== | ||
[[Prawo]] malejących [[Przychody|przychodów]] powoduje, że [[produkt]] krańcowy rośnie, osiągając maximum, po czym po prostu musi już maleć. | |||
Właśnie dlatego koszt krańcowy zmniejsza się aż osiągnie minimum, a następnie rośnie (krzywa ta - kosztów krańcowych jest odwrotnością krzywej produkcyjności krańcowej). Dopóki produkt krańcowy jest rosnący, to koszty krańcowe spadają. Natomiast jeśli produkt krańcowy jest malejący to koszty krańcowe rosną. W sytuacji, gdy produkt krańcowy jest największy to koszty krańcowe osiągają minimum. | |||
Miara geometryczną kosztów krańcowych jest tangens kąta utworzonego przez styczną do krzywej kosztów całkowitych i oś odciętych (Dach Z. 2012, s. 172). | |||
Miara geometryczną kosztów krańcowych jest tangens kąta utworzonego przez styczną do krzywej kosztów całkowitych i oś odciętych | |||
==Krzywa kosztu krańcowego (MC)== | ==Krzywa kosztu krańcowego (MC)== | ||
Kształt krzywej MC wynika bezpośrednio z prawa malejących przychodów. Początkowo przy zwiększaniu ilości zużywanych zmiennych czynników produkcji, koszt wytworzenia dodatkowych jednostek produkcji jest niższy od kosztu jednostek poprzednich. MC maleje. | |||
Powyżej pewnego poziomu produkcji pojawiają się malejące [[przychody]]. Od tego poziomu MC rośnie. | |||
Powyżej pewnego poziomu produkcji pojawiają się malejące [[przychody]]. Od tego poziomu MC rośnie. | |||
Wytworzenie dodatkowych jednostek produkcji kosztuje coraz więcej, gdyż [[potrzeba]] do tego coraz większych ilości zmiennych czynników produkcji. | Wytworzenie dodatkowych jednostek produkcji kosztuje coraz więcej, gdyż [[potrzeba]] do tego coraz większych ilości zmiennych czynników produkcji. | ||
| Linia 50: | Linia 34: | ||
[[Plik:Koszt_krańcowy.jpg|300px|right|thumb|Rys. 1 Koszt krańcowy]] | [[Plik:Koszt_krańcowy.jpg|300px|right|thumb|Rys. 1 Koszt krańcowy]] | ||
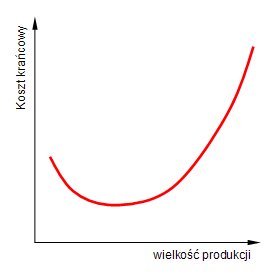
Jak można zaobserwować (rys. 1) wykresem kosztów krańcowych jest krzywa, która najpierw maleje, osiąga wielkość minimalna (najmniejszą) a następnie wznosi się ku górze. Dzieje się tak na skutek "prawa nieproporcjonalnych przychodów" (Beksiak, 2001, s. 70). Jeżeli kolejne [[nakłady]] czynnika zmiennego dają do pewnego punktu rosnące przyrosty produkcji, a następnie [[przychody]] malejące, to koszt wytworzenia tej dodatkowej produkcji zmienia się odwrotnie: najpierw maleje, a później rośnie (Beksiak, 2001, s. 71). | Jak można zaobserwować (rys. 1) wykresem kosztów krańcowych jest krzywa, która najpierw maleje, osiąga wielkość minimalna (najmniejszą) a następnie wznosi się ku górze. Dzieje się tak na skutek "prawa nieproporcjonalnych przychodów" (Beksiak, 2001, s. 70). Jeżeli kolejne [[nakłady]] czynnika zmiennego dają do pewnego punktu rosnące przyrosty produkcji, a następnie [[przychody]] malejące, to koszt wytworzenia tej dodatkowej produkcji zmienia się odwrotnie: najpierw maleje, a później rośnie (Beksiak, 2001, s. 71). | ||
Wzrost kosztu krańcowego prowadzi do zmniejszenia produkcji danego dobra | Wzrost kosztu krańcowego prowadzi do zmniejszenia produkcji danego dobra (Nojszewska A. 2010, s. 117) | ||
==Koszt krańcowy a koszt przeciętny== | ==Koszt krańcowy a koszt przeciętny== | ||
Podczas gdy koszt krańcowy jest mniejszy od przeciętnego kosztu całkowitego, przeciętny koszt całkowity maleje. Natomiast gdy koszt krańcowy jest większy od przeciętnego kosztu całkowitego, przeciętny koszt całkowity rośnie. To nie jest wcale zbieg okoliczności - jest to zależność matematyczna. Ten związek między przeciętnym kosztem całkowitym i kosztem krańcowym skutkuje tym, że krzywa kosztu krańcowego przecina krzywą przeciętnego kosztu całkowitego. Punkt przecięcia to punkt minimum. Jest to spowodowane faktem, że przy niskim poziomie produkcji przeciętny koszt całkowity jest większy od kosztu krańcowego, więc maleje z każdą dodatkowa jednostką. (Mankiw N.G, Taylor M.P 2015, s. 224) | |||
Podczas gdy koszt krańcowy jest mniejszy od przeciętnego kosztu całkowitego, przeciętny koszt całkowity maleje. Natomiast gdy koszt krańcowy jest większy od przeciętnego kosztu całkowitego, przeciętny koszt całkowity rośnie. To nie jest wcale zbieg okoliczności - jest to zależność matematyczna. Ten związek między przeciętnym kosztem całkowitym i kosztem krańcowym skutkuje tym, że krzywa kosztu krańcowego przecina krzywą przeciętnego kosztu całkowitego. Punkt przecięcia to punkt minimum. Jest to spowodowane faktem, że przy niskim poziomie produkcji przeciętny koszt całkowity jest większy od kosztu krańcowego, więc maleje z każdą dodatkowa jednostką. (Mankiw N.G, Taylor M.P 2015, s. 224) | Po przecięciu się tych dwóch krzywych sytuacja ulega zmianie - dokładniej odwróceniu i zgodnie z wcześniejszymi wyjasnieniami przeciętny koszt całkowity zaczyna od tego punktu rosnąć. [[Wartość]] w punkcie przecięcia - > koszt przeciętny jest równy kosztowi wytworzenia dodatkowej jednostki, więc nie zmienia się przy wzroście produkcji i osiąga wartość minimalna. | ||
Po przecięciu się tych dwóch krzywych sytuacja ulega zmianie - dokładniej odwróceniu i zgodnie z wcześniejszymi wyjasnieniami przeciętny koszt całkowity zaczyna od tego punktu rosnąć. [[Wartość]] w punkcie przecięcia -> koszt przeciętny jest równy kosztowi wytworzenia dodatkowej jednostki, więc nie zmienia się przy wzroście produkcji i osiąga wartość minimalna. | |||
==Przykład praktyczny== | ==Przykład praktyczny== | ||
| Linia 65: | Linia 48: | ||
Dlaczego jednak przyrost kosztów jest dzielony przez 1 ? W sytuacji podanej w przykładzie, kiedy produkcja wzrasta o jednostkę, oczywiście jest to bez znaczenia. Koszt krańcowy jest tutaj po prostu przyrostem związanym z wytworzeniem dodatkowej jednostki. Są jednak przypadki, kiedy produkcja może wzrosnąć jedynie o całą partię produktu. | Dlaczego jednak przyrost kosztów jest dzielony przez 1 ? W sytuacji podanej w przykładzie, kiedy produkcja wzrasta o jednostkę, oczywiście jest to bez znaczenia. Koszt krańcowy jest tutaj po prostu przyrostem związanym z wytworzeniem dodatkowej jednostki. Są jednak przypadki, kiedy produkcja może wzrosnąć jedynie o całą partię produktu. | ||
{{infobox5|list1={{i5link|a=[[Koszt całkowity]]}} — {{i5link|a=[[Użyteczność krańcowa]]}} — {{i5link|a=[[Produkt krańcowy]]}} — {{i5link|a=[[Linia ograniczenia budżetowego]]}} — {{i5link|a=[[Krańcowa stopa substytucji]]}} — {{i5link|a=[[Dochód realny]]}} — {{i5link|a=[[Utarg]]}} — {{i5link|a=[[Efekt dochodowy i substytucyjny]]}} — {{i5link|a=[[Przychód krańcowy]]}} }} | |||
==Bibliografia== | ==Bibliografia== | ||
* Begg D., Fischer S., Dornbusch R. ( | <noautolinks> | ||
* Beksiak J. red. (2001) | * Begg D., Fischer S., Dornbusch R. (2007), ''Ekonomia. Makroekonomia'', Polskie Wydawnictwo Ekonomiczne, Warszawa | ||
* Bergstrom T | * Beksiak J. (red.) (2001), ''Ekonomia'', Wydawnictwo Naukowe PWN, Warszawa | ||
* Dach Z. (2012) | * Bergstrom T., Varian H. (2003), ''Mikroekonomia - ćwiczenia'', Wydawnictwo Naukowe PWN, Warszawa | ||
* Klimczak B. ( | * Dach Z. (2012), ''Mikroekonomia'', Wydawnictwo Uniwersytetu Ekonomicznego w Krakowie, Kraków | ||
* Mankiw N | * Klimczak B. (2006), ''Mikroekonomia'', Wydawnictwo Akademii Ekonomicznej im. Oskara Langego, Wrocław | ||
* Milewski R. (red.) ( | * Mankiw N., Taylor M. (2015), ''Mikroekonomia'', Polskie Wydawnictwo Ekonomiczne, Warszawa | ||
* Nojszewska E. (2010) | * Milewski R., Kwiatkowski E. (red.) (2016), ''Podstawy ekonomii'', Wydawnictwo Naukowe PWN, Warszawa | ||
* Skarżyńska A. (2011) | * Nojszewska E. (2010), ''Podstawy Ekonomii'', Wydawnictwo Szkolne i Pedagogiczne, Warszawa | ||
* Skarżyńska A. (2011), ''Skala produkcji rolniczych działalności produkcyjnych a ich opłacalność'', Roczniki nauk rolniczych, T.98, z. 1 | |||
</noautolinks> | |||
{{a|Agnieszka Ruszkowska, Robert Stelmaczonek, Magdalena Kucypera}} | {{a|Agnieszka Ruszkowska, Robert Stelmaczonek, Magdalena Kucypera}} | ||
[[Kategoria:Koszt]] | |||
{{#metamaster:description|Koszt krańcowy to wzrost kosztów całkowitych przy produkcji jednostki więcej.}} | |||
Aktualna wersja na dzień 19:09, 1 gru 2023
Koszt krańcowy - inaczej koszt marginalny (ang. marginal cost, MC) jest to wzrost kosztów całkowitych wywołany wzrostem produkcji o jednostkę (Begg, 2003, s. 179). Inaczej mówiąc, jest to koszt wyprodukowania kolejnej (dodatkowej) jednostki dobra, wykonaniem danej czynności lub świadczeniem usługi.
Jest to różnica pomiędzy kosztem całkowitym dwóch sąsiednich wielkości produkcji (Beksiak, 2001, s. 70), albo inaczej można powiedzieć jest to przyrost kosztu (zmiennego bo stały z definicji się nie zmienia) jeśli produkcja zmieni się o jednostkę. Koszty krańcowe są związane tylko z kosztami zmiennym, ponieważ koszty stałe nie zmieniają się wraz z rosnącą produkcją. Dlatego właśnie dla rozmiarów oraz zmian kosztu krańcowego - stała cześć sumy kosztów pozostaje bez znaczenia (w przeciwieństwie do kosztu przeciętnego - tam odgrywa dużą rolę).
Przyjmując za podstawę koszt przeciętny, suma kosztów całkowitych będzie iloczynem kosztu przeciętnego oraz ilości wytworzonego produktu. Przyjmując natomiast za podstawę koszt krańcowy - suma kosztów całkowitych będzie suma kolejnych kosztów krańcowych powiększoną o koszty stałe (Dach Z. 2012, s. 172).
TL;DR
Koszt krańcowy to wzrost kosztów całkowitych spowodowany wzrostem produkcji o jednostkę. Jest to różnica między kosztem całkowitym dwóch sąsiednich wielkości produkcji. Koszty krańcowe są związane tylko z kosztami zmiennymi. Krzywa kosztu krańcowego najpierw maleje, osiąga minimum, a następnie rośnie. Koszt krańcowy jest mniejszy od przeciętnego kosztu całkowitego, gdy ten maleje, i większy, gdy ten rośnie. Przy wzroście produkcji przeciętny koszt całkowity najpierw maleje, a potem rośnie.
Geneza
Pojęcie kosztów krańcowych po raz pierwszy pojawiło się w rozważaniach David'a Ricardo (1772-1823) w jego ekonomicznych rozważaniach na temat renty i prawa malejących przychodów (Turgot, 1765r.).
Ricardo analizując rentę z majątku ziemskiego od strony kosztów produkcji zdefiniował koszty krańcowe. Stwierdził, że koszty produkcji zboża rosną w miarę, jak ziemia jest uprawiana bardziej intensywnie. Ostatecznie stwierdził, że koszt krańcowy to łączny przyrost kosztu niezbędnego do wytworzenia dodatkowej ilości końcowego produktu.
Jest to początek znanej i uprawianej do dzisiaj szkoły rachunku marginalnego, której istotą nie są wartości globalne lecz jej przyrosty i warunki ich zmian.
Prawo malejących przychodów
Prawo malejących przychodów powoduje, że produkt krańcowy rośnie, osiągając maximum, po czym po prostu musi już maleć. Właśnie dlatego koszt krańcowy zmniejsza się aż osiągnie minimum, a następnie rośnie (krzywa ta - kosztów krańcowych jest odwrotnością krzywej produkcyjności krańcowej). Dopóki produkt krańcowy jest rosnący, to koszty krańcowe spadają. Natomiast jeśli produkt krańcowy jest malejący to koszty krańcowe rosną. W sytuacji, gdy produkt krańcowy jest największy to koszty krańcowe osiągają minimum.
Miara geometryczną kosztów krańcowych jest tangens kąta utworzonego przez styczną do krzywej kosztów całkowitych i oś odciętych (Dach Z. 2012, s. 172).
Krzywa kosztu krańcowego (MC)
Kształt krzywej MC wynika bezpośrednio z prawa malejących przychodów. Początkowo przy zwiększaniu ilości zużywanych zmiennych czynników produkcji, koszt wytworzenia dodatkowych jednostek produkcji jest niższy od kosztu jednostek poprzednich. MC maleje.
Powyżej pewnego poziomu produkcji pojawiają się malejące przychody. Od tego poziomu MC rośnie.
Wytworzenie dodatkowych jednostek produkcji kosztuje coraz więcej, gdyż potrzeba do tego coraz większych ilości zmiennych czynników produkcji.
Jak można zaobserwować (rys. 1) wykresem kosztów krańcowych jest krzywa, która najpierw maleje, osiąga wielkość minimalna (najmniejszą) a następnie wznosi się ku górze. Dzieje się tak na skutek "prawa nieproporcjonalnych przychodów" (Beksiak, 2001, s. 70). Jeżeli kolejne nakłady czynnika zmiennego dają do pewnego punktu rosnące przyrosty produkcji, a następnie przychody malejące, to koszt wytworzenia tej dodatkowej produkcji zmienia się odwrotnie: najpierw maleje, a później rośnie (Beksiak, 2001, s. 71).
Wzrost kosztu krańcowego prowadzi do zmniejszenia produkcji danego dobra (Nojszewska A. 2010, s. 117)
Koszt krańcowy a koszt przeciętny
Podczas gdy koszt krańcowy jest mniejszy od przeciętnego kosztu całkowitego, przeciętny koszt całkowity maleje. Natomiast gdy koszt krańcowy jest większy od przeciętnego kosztu całkowitego, przeciętny koszt całkowity rośnie. To nie jest wcale zbieg okoliczności - jest to zależność matematyczna. Ten związek między przeciętnym kosztem całkowitym i kosztem krańcowym skutkuje tym, że krzywa kosztu krańcowego przecina krzywą przeciętnego kosztu całkowitego. Punkt przecięcia to punkt minimum. Jest to spowodowane faktem, że przy niskim poziomie produkcji przeciętny koszt całkowity jest większy od kosztu krańcowego, więc maleje z każdą dodatkowa jednostką. (Mankiw N.G, Taylor M.P 2015, s. 224) Po przecięciu się tych dwóch krzywych sytuacja ulega zmianie - dokładniej odwróceniu i zgodnie z wcześniejszymi wyjasnieniami przeciętny koszt całkowity zaczyna od tego punktu rosnąć. Wartość w punkcie przecięcia - > koszt przeciętny jest równy kosztowi wytworzenia dodatkowej jednostki, więc nie zmienia się przy wzroście produkcji i osiąga wartość minimalna.
Przykład praktyczny
Przedsiębiorstwo produkuje 100 jednostek produktu po koszcie 200 zł.Wzrost produkcji do 101 jednostek powoduje wzost kosztów całkowitych do 203 zł. Tak więc koszt krańcowy (MC) ostatniej wytworzonej jednostki wynosi 3 zł. Podstawiając liczby do wzoru, otrzymujemy:
Dlaczego jednak przyrost kosztów jest dzielony przez 1 ? W sytuacji podanej w przykładzie, kiedy produkcja wzrasta o jednostkę, oczywiście jest to bez znaczenia. Koszt krańcowy jest tutaj po prostu przyrostem związanym z wytworzeniem dodatkowej jednostki. Są jednak przypadki, kiedy produkcja może wzrosnąć jedynie o całą partię produktu.
| Koszt krańcowy — artykuły polecane |
| Koszt całkowity — Użyteczność krańcowa — Produkt krańcowy — Linia ograniczenia budżetowego — Krańcowa stopa substytucji — Dochód realny — Utarg — Efekt dochodowy i substytucyjny — Przychód krańcowy |
Bibliografia
- Begg D., Fischer S., Dornbusch R. (2007), Ekonomia. Makroekonomia, Polskie Wydawnictwo Ekonomiczne, Warszawa
- Beksiak J. (red.) (2001), Ekonomia, Wydawnictwo Naukowe PWN, Warszawa
- Bergstrom T., Varian H. (2003), Mikroekonomia - ćwiczenia, Wydawnictwo Naukowe PWN, Warszawa
- Dach Z. (2012), Mikroekonomia, Wydawnictwo Uniwersytetu Ekonomicznego w Krakowie, Kraków
- Klimczak B. (2006), Mikroekonomia, Wydawnictwo Akademii Ekonomicznej im. Oskara Langego, Wrocław
- Mankiw N., Taylor M. (2015), Mikroekonomia, Polskie Wydawnictwo Ekonomiczne, Warszawa
- Milewski R., Kwiatkowski E. (red.) (2016), Podstawy ekonomii, Wydawnictwo Naukowe PWN, Warszawa
- Nojszewska E. (2010), Podstawy Ekonomii, Wydawnictwo Szkolne i Pedagogiczne, Warszawa
- Skarżyńska A. (2011), Skala produkcji rolniczych działalności produkcyjnych a ich opłacalność, Roczniki nauk rolniczych, T.98, z. 1
Autor: Agnieszka Ruszkowska, Robert Stelmaczonek, Magdalena Kucypera