Izokwanta

Izokwanta
Polecane artykuły
Krzywa możliwości produkcyjnych Funkcja użyteczności Produkt krańcowy Korzyści skali Funkcja produkcji Teoria kosztów absolutnych Koszt zmienny Teoria obfitości zasobów Elastyczność

Izokwanta (krzywa jednakowego produktu) jest zbiorem możliwych kombinacji nakładu dwóch czynników produkcji, które pozwalają efektywnie wytworzyć daną wielkość produktu.

Izokwanty swym wyglądem przypominają krzywe obojętności. Istnieje jednak zasadnicza różnica między nimi, gdyż izokwanty są oznaczone ilością produktu, jaka im odpowiada, a nie poziomami użyteczności jak jest w przypadku krzywych obojętności (H. R. Varian, 2002, s. 339)

Interpretacja

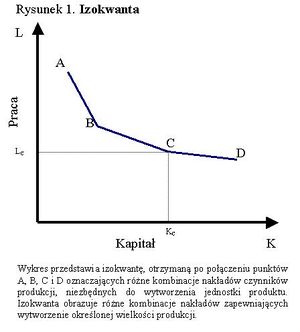
Poszczególne punkty na izokwancie odzwierciedlają różne metody wytwarzania takiej samej ilości produktu. Każdy punkt na izokwancie reprezentuje inną metodę wytwarzania - od metod najbardziej kapitałochłonnych do najbardziej pracochłonnych.

Umiejscowienie kilku izokwant na wykresie pokazuje nam swoistą mapę. Każda izokwanta pokazuje różne kombinacje nakładów wykorzystanych w procesie produkcji w celu wytworzenia danej wielkości produktu.

Rodzaje Substytucji

Izokwanty w zależności od kształtu krzywej możemy wyróżnić na:

• Substytucje pełną - jeden czynnik wytwórczy może być zastąpiony przez drugi czynnik wytwórczy. Całkowita swoboda podmieniania jednego czynnika drugim. W substytucji pełnej może wystąpić sytuacja, w której czynniki produkcji będą względem siebie znakomitymi substytutami. Oznacza to, że zastępowanie czynników względem siebie odbywa się w określonej proporcji, np. 1:1. W takiej sytuacji izokwanta jest opadająca krzywa liniową. Występuje również sytuacja w której produkcja może być wyrabiana przy stałym stosunku ilościowym. Taką izokwantę określamy krzywą doskonałej komplementarności. Ma ona kształt ramienia kąta prostego.
• Substytucję niepełną - żaden z czynników wytwórczych nie może być całkowicie zastąpiony przez drugi czynnik wytwórczy. Krzywa nie dotyka osi współrzędnych. Im wyższy jest stopień substytucji, tym silniej krzywa będzie uwypuklać się w kierunku początku układu współrzędnych (Z.Dach, 2001, s. 139)

W substytucji niepełnej każdy z czynników musi być wytwarzany w określonej wielkości, żadnego z nich nie można całkowicie zastąpić. Mała swoboda podmieniania jednego czynnika drugim z powodu na brak możliwości całkowitego zrezygnowania z wytwarzania obu czynników wytwórczych.

Cechy

Izokwanty charakteryzują się trzema cechami:

• Ponieważ każda z nich odnosi się do różnej wielkości produkcji nie mogą się przecinać między sobą.

• Wszystkie izokwanty mają nachylenie ujemne. Wynika to z faktu, iż każde przedsiębiorstwo dysponując ograniczonymi zasobami czynników produkcji i chcąc wytworzyć daną wielkość produkcji, rozważy zmianę technologii na bardziej kapitałochłonną tylko wówczas gdy pozwoli to na zmniejszenie nakładów pracy i na odwrót.
• Poszczególne izokwanty stopniowo ulegają "spłaszczeniu" w miarę przesuwania się po nich w prawo, co jest efektem angażowania coraz większej dodatkowej ilości kapitału w celu zrównoważenia kolejnych takich samych obniżek nakładów pracy potrzebnych do wytworzenia wciąż takiej samej ilości produktu (D. Begg 2003, s. 334)

Podsumowując izokwanta jest to geometryczne miejsce takich ilościowych kombinacji czynników produkcji, które zapewniają jednakowy poziom produkcji (produktu). (A. Becla 2001, s. 151)

Zastosowanie

Izokwanta potrzebna jest Do policzenia m.in.:

• Optimum produkcji, jest to "optymalna kombinacja czynników znajduje się punkcie styczności linii jednakowego kosztu z możliwie najwyżej położoną izokwantą produkcji. Jest to punkt równowagi przedsiębiorstwa osiągający maksymalna produkcje". (M. Rekowski 2002, s. 161)
• Ścieżki ekspansji produktu, jest to "krzywa która łączy punkty styczności między izokwantami produkcji oraz równoległymi liniami jednostkowymi kosztów. Punkty te oznaczają optymalne kombinacje czynników odpowiadające różnym poziomom produkcji" (M. Rekowski 2002, s. 164)

Bibliografia

• Becla A., Czaja S., Hałasa J. M., Rumianowska I. (2001), Elementy Mikroekonomii, Wydawnictwo I-BiS, Wrocław
• Begg D., Fisher S., Vernasca G., Dornbusch R. (2014), Ekonomia: Makroekonomia, Polskie Wydawnictwo Ekonomiczne, Warszawa
• Dach Z. (2001), Podstawy mikroekonomii, Wydawnictwo Naukowe SYNABA, Kraków
• Nojszewska E. (2015),Ekonomiczna analiza efektywności szpitaliMyśl Ekonomiczna i Polityczna, nr.2
• Rekowski M. (2002), Wprowadzenie do mikroekonomii, WROKOP, Poznań
• Varian Hal R. (2002), Mikroekonomia, kurs średni - ujęcie nowoczesne, PWN, Warszawa
• Zalega T. (2011), Mikroekonomia Współczesna, WWZ, Warszawa

Autor: Kamil Czerwonka i Robert Dzień