Fraktal
Fraktal (ang. fractal) to obiekt samo-podobny z nieskończoną liczbą detali. Kształty te ułożone są w każdy możliwy sposób i można je spotkać praktycznie wszędzie. Są nieregularne, łączą ze sobą wiele rozmaitych kształtów czy figur, nie są "idealnie" proste jak np. figury, których uczymy się od początku uczęszczania do szkoły. W naturze przeważają właśnie fraktale. Mają one swoje zastosowanie w takich naukach jak matematyka, fizyka czy informatyka. Dzięki nim nastała nowa generacja w geometrii, a nawet w architekturze, gdzie architekci w końcu odnaleźli coś, co pomogło im odejść od prostych, tradycyjnych kształtów i wykorzystali to w swoich projektach. "Ostatecznie fraktal od łacińskiego słowa fractus - ‘złamany’ to figura geometryczna o złożonej strukturze, niebędąca krzywą powierzchnią, ani bryłą w znaczeniu geometrii klasycznej, mająca wymiar ułamkowy; Przy opisywaniu konstrukcji fraktali daje się zauważyć, że są one takie same w każdym kawałku i w każdej skali; Tę cechę nazywa się często samopodobieństwem" (W. Kamiński, R. Kotowski, P. Tronczyk 2010, s. 266). Fraktale charakteryzują się następującymi cechami:
- samopodobieństwo: każdy fragment fraktalny jest identyczny,
- holograficzność,
- można je powiększać i pomniejszać w nieskończoność,
- fraktale geometryczne powstają w wyniku dowolnej liczby powtórzeń określonej operacji matematycznej.
TL;DR
Fraktale są obiektami samo-podobnymi, które występują w naturze i mają zastosowanie w matematyce, fizyce i informatyce. Przedsiębiorstwo fraktalne to jednostka organizacyjna, która działa samodzielnie i ma podobne cechy do fraktala. Fraktale są ważne w geometrii, a ich wymiar fraktalny jest kluczowy. Analiza fraktalna jest wykorzystywana w przewidywaniu zmian na rynku kapitałowym, a wymiar fraktalny jest istotny w ocenie ryzyka finansowego.
Przedsiębiorstwo fraktalne
Fraktal jest jednostką przedsiębiorstwa, która może działać samodzielnie, a jej cele mają być opisany w ten sam sposób. "Fraktalem może być zarówno przedsiębiorstwo (makrofraktal), jak i jego jednostki organizacyjne (mikrofraktale). Makrofraktal (przedsiębiorstwo) oraz mikrofraktale (jednostki organizacyjne) charakteryzują się następującymi cechami:
- strukturalne podobieństwo,
- samoorganizacja,
- dynamika,
- witalność,
- duża swoboda decyzyjna,
- w długim okresie mogą funkcjonować względnie niezależnie,
- samonawigowanie zorientowane na kreowanie wartości dodanej dla klienta,
- wartość dodana generowana przez przedsiębiorstwo nie jest prostą sumą wartości dodanych wytworzonych przez jednostki organizacyjne" (K. Perechuda 2000, s. 26).
Funkcjonowanie fraktali wiąże się z pewnymi zasadami i instrumentami, które je napędzają i nimi kierują. Po pierwsze fraktale są jednostkami, które ulegają ciągłej przemianie i realizują wiele projektów wpływających na ich strukturę organizacyjną. Po drugie, tworząc duże przedsiębiorstwo czy koncern są zdolne do nawigowania samych siebie, tzn. podejmowania decyzji odnośnie funkcjonowania i sterowania zdarzeniami zachodzącymi u nich. Po trzecie, we fraktalach nie ma podziału na szef - pracownik, poziom wyższy i niższy. Tutaj relacje się pokrywają i współgrają. Co więcej, każdy z pracowników jest dla siebie szefem. Nacisk jest nałożony na satysfakcję z pracy, a nie dążenie do jak najlepszego efektu tylko po to, aby końcowy efekt (wynagrodzenie) było wysokie. Kolejną zasadą jest funkcjonowanie fraktali wg zasad panujących "wewnątrz". Zewnętrzne bodźce nie mogą mieć wpływu na to co się dzieje wewnątrz. Dzięki temu działa on sprawniej i efektywniej.
Fraktal w geometrii
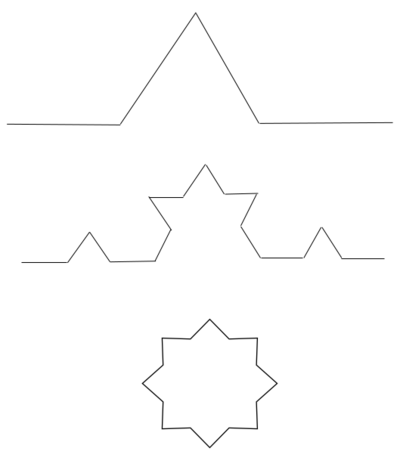
Fraktal odgrywa ważną rolę w dziedzinie matematyki jaką jest geometria. "Klasyczne pojęcie wymiaru, stworzone przez topologię, zna wymiar przybierający wartości całkowite, do którego jesteśmy przyzwyczajeni i z którym stykamy się na co dzień w opisach geometrycznych. […] Fraktale mają również wymiar ułamkowy, zwany też wymiarem fraktalnym lub wymiarem Hausdorffa. Ten wymiar ułamkowy to najważniejsza cecha fraktala" (S. Romanowski, D. Światła - Wójcik 2011, s. 100). Płatki śniegu, które doskonale znamy, są fraktalami Kocha. Powstaje on w ten sposób, że odcinek dzielimy na 3 części, pozbywamy się części środkowej i wstawiamy tam trójkąt równoboczny. Dzięki temu z odcinka o długości 3 powstaje figura o długości 4. Później powtarzamy tę czynność i powstaje nam rodzaj pętli, która zamyka się po kilku takich akcjach i dostajemy fraktal w postaci płatka śniegu. Poniższy rysunek przedstawia ten fraktal.
Analiza fraktalna
Prognozy finansowe przeprowadzano w dawnych czasach za pomocą modeli liniowych. Jednak światowy kryzys w 1987 roku doprowadził do spadku indeksów giełdowych na całym świecie, w związku z czym zaczęto poszukiwać nowych metod pomagających przewidzieć zmiany na rynku kapitałowym. Doprowadziło to do zastosowania analizy fraktalnej. "Wykorzystanie analizy fraktalnej w badaniach właściwości szeregów czasowych notowań giełdowych pozwala szacować prawdopodobieństwo określonych ruchów rynku kapitałowego oraz określić wymiar zbiorów granicznych układu dynamicznego opisującego jego zachowanie (Z. Rzeszótko 2016, s. 132).
Wymiar fraktalny
Zagadnienia występujące w obrębie fraktali dotyczą również kwestii oceny ryzyka i podejmowanych decyzji inwestycyjnych, tj. lokowanie kapitałów na rynku finansowym. "Pojęciem kluczowym w badaniu finansowych szeregów czasowych w ujęciu fraktalnym jest wymiar fraktalny. To obszerne określenie obejmuje całe spektrum rozmaitych miar, z których każda opisuje strukturę badanych obiektów" (R. Buła 2017, s. 11). "Wymiar fraktalny jest uogólnieniem wymiaru euklidesowego i służy do opisu skomplikowanych strukturalnie obiektów geometrycznych, np. szeregów czasowych. Wymiar ten bada, w jakim stopniu analizowany obiekt (szereg) wypełnia przestrzeń, w której jest zanurzony. Jego cechą charakterystyczną jest to, że może on przyjmować wartości niecałkowite" (K. Zeug - Żebro 2017, s. 80).
| Fraktal — artykuły polecane |
| Indeks — Zasada Pareto — Metoda Monte Carlo — Miary ryzyka — Baza danych — Ciąg Fibonacciego — Drzewo decyzyjne — Badanie panelowe — Algorytm genetyczny |
Bibliografia
- Buła R. (2017), Analiza Wymiaru fraktalnego spółek notowanych na giełdzie papierów wartościowych w Warszawie - aspekty metodyczne, Uniwersytet Ekonomiczny w Katowicach
- Kamiński W., Kotowski R., Tronczyk P. (2010), Użytkowanie komputerów, Wydawnictwo Polsko - Japońskiej Akademii Technik Komputerowych
- Perechuda K. (red.) (2000), Zarządzanie przedsiębiorstwem przyszłości. Koncepcje, modele, metody, Wydawnictwo Placet, Warszawa
- Romanowski S., Światła-Wójcik D. (2011), Symulacje komputerowe w fizyce i chemii, Akademia Humanistyczno Ekonomiczna
- Rzeszótko Z. (2016), Metody ilościowe w badaniach ekonomicznych, Katedra Ekonometrii i Statystyki SGGW, Warszawa
- Zeug-Żebro K. (2017), Analiza wpływu zastosowania redukcji poziomu szumu losowego na poziom ryzyka inwestycyjnego Zeszyty Naukowe Uniwersytetu Ekonomicznego w Katowicach, nr 335
Autor: Patrycja Rygiel