Teoria gier

Teoria gier
Polecane artykuły
Strategia BATNA Prawdopodobieństwo Kryteria oceny Modele procesów decyzyjnych Analytic Hierarchy Process Korzystność Test Turinga Teoria oczekiwań Metoda simpleks

Teoria gier jest to matematyczna teoria rozwiązywania sytuacji konfliktowych bądź współpracy, w których wynik uzyskany przez jedną osobę zależy on decyzji podjętych przez innych. Teorię tę po raz pierwszy opracowali John von Neuman i Oskar Morgenstern w opublikowanej w 1944 r. pracy pt. "Teoria gier i zachowanie ekonomiczne". Teoria ta pozwala analizować i przewidywać działania uczestników gry, przy założeniu, że podejmują oni racjonalne decyzje, czyli nastawione na realizację celów, prowadzące do maksymalizacji zysków, oraz znają reguły gry. Dla gier dwuosobowych można zbudować prostą macierz wypłat (tzn. wyników) zależących od tego jaką strategię wybiorą gracze.

TL;DR

Teoria gier to matematyczna teoria analizująca sytuacje konfliktowe i współpracy, gdzie wynik zależy od decyzji podjętych przez uczestników. Gra składa się z graczy, strategii, funkcji wypłat i wypłat. Gry mogą być dwuosobowe, wieloosobowe, kooperacyjne, o sumie zerowej, strategiczne lub ekstensywne. Istnieją różne rodzaje strategii, takie jak strategie bezpieczeństwa, czyste i mieszane. Gry mogą być przedstawiane w postaci rozwiniętej lub normalnej. Gry o sumie zerowej są często przedstawiane za pomocą macierzy wypłat. Teoria gier znajduje zastosowanie w wielu dziedzinach, takich jak psychologia, socjologia, ekonomia i polityka. Równowaga Nasha występuje, gdy optymalne strategie jednego gracza są znane innym, a zmiana strategii nie poprawia sytuacji danego gracza.

Elementy składowe gier

Każda gra składa się z elementów takich jak (Haman J. 2014, s.31):

• zbiór graczy (agentów), który nie może liczyć mniej niż 2 osoby. Muszą oni postępować w sposób racjonalny i dążyć do maksymalizacji swoich wypłat.
• zbór strategii, czyli ruchów przypisanych indywidualnie do każdego z graczy.
• funkcji, która przypisuje "wypłaty w zależności od kombinacji strategii użytych przez graczy.
• wypłaty, która jest korzyścią osiąganą z tytułu wyniku gry. Z reguły przedstawia się ją w postaci tabeli albo macierzy.

Typy gier

Gry można podzielić według następujących kryteriów:

• gry dwuosobowe i wieloosobowe
• gry kooperatywne - gracze mogą porozumiewać się między sobą i zawierać koalicje (w przeciwieństwie do gier niekooperatywnych, gdzie jest to zabronione)
• gry o sumie zerowej - jeden z graczy otrzymuje dokładnie tyle ile drugi gracz musi oddać. Jeżeli ten warunek nie zostanie zachowany mówimy wtedy o grze niezerowej.
• gry strategiczne (gdzie gracze podejmują decyzję jednocześnie) i gry ekstensywne (decyzje podejmowane są przez graczy na przemian)

Strategie

Strategią nazywa się plan działania gracza, jego reakcję na każdą możliwą sytuację. Dzieli się je na strategie (Watson J. 2011 s.53 i 67; Haman J.2014 s. 45-46):

• bezpieczeństwa - gwarantuje wypłatę, która nie jest zależna od strategii przeciwnika.
• czystą- polega na tym,że prawdopodobieństwo wyboru strategii przez gracza wynosi 1, a wybrana strategia pozostaje niezmienna.
• mieszaną-polega na ocenie przez gracza jego własnych zachowań, każdemu wyborowi przypisane jest prawdopodobieństwo z jakim zostanie dokonany.

Ze względu na stopień dominacji można również podzielić strategie na:

• dominujące - są one lepsze od pozostałych strategii danego gracza, niezależnie od wyboru strategii przez przeciwnika
• zdominowane - są one nie lepsze od pozostałych strategii, jednak nie warto ich rozpatrywać ze względu na fakt, że istnieją takie, które dadzą lepszy wynik.

Gry w postaci rozwiniętej i normalnej

Rozwinięta postać gry:

Metoda zapisu polega na wykreśleniu drzewa gry. Drzewo takie musi spełniać następujące warunki:

• zawiera jeden wierzchołek
• każdy wewnętrzny węzeł przypisany jest graczowi
• Krawędzie wychodzące z wierzchołka oznaczają możliwe strategie gracza
• skończona liczba liści (węzłów końcowych) wraz z przypisanymi im wypłatami, zapisanymi w postaci (w₁, w₂,...w_n), gdzie w_i oznacza wypłatę dla i-tego gracza.

Normalna postać gry:

Sposób ten wykorzystuje fakt, że każdą grę możemy opisać za pomocą strategii i wypłat im odpowiadających. Dzięki tej metodzie nie musimy pamiętać całego drzewa ruchów (co ma miejsce w przypadku rozwiniętej postaci gry) i pozwala się skupić tylko na analizie wypłat przy pewnych kombinacjach strategii graczy.

Macierz wypłat

Gry o sumie zerowej najlepiej jest przedstawić w postaci macierzy wypłat. Zawiera ona wartości wypłat dla wszystkich możliwych kombinacji strategii obu graczy.

Rys. 1. Dylemat więźnia

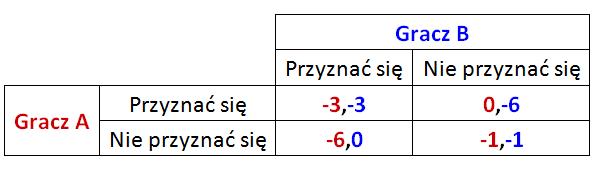
Dylemat więźnia

Dylemat więźnia to jedna z popularniejszych gier, którą w 1950 roku wymyślili Melvin Dresher i Merrill Flood z RAND Corporation i nosi nazwę 12.1. Przedstawia sytuację, gdy dwóch oskarżonych o wspólne popełnienie przestępstwa jest przesłuchiwanych oddzielnie, każdy z nich zastał poinformowany o wyroku zależącym od tego co obaj oskarżeni wybiorą: "przyznać się" czy "nie przyznać się".

Strategia dominująca

Ze strategią dominującą mamy do czynienia, gdy jeden z graczy może określić korzystniejszy dla siebie wybór niezależnie od tego, którą strategię wybierze drugi gracz. W dylemacie więźnia, jeśli gracz A przyzna się, to korzystniejsze dla gracza B jest przyznać się, natomiast gdy A nie przyzna się, to ponownie dla B lepiej jest się przyznać. Strategia "przyznać się" jest więc dla gracza B strategią dominującą. W analogicznej sytuacji jest gracz A, z czego wynika, że w tej grze występuje dominująca równowaga (mówimy o niej gdy wszyscy gracze mogą określić strategię dominującą).

Zasada minimaksu

Strategia zastosowana w grze, która ma na celu przyniesienie maksymalnego zysku nie jest racjonalna, ponieważ każdy rozsądny gracz z łatwością ją przewidzi i skutecznie zablokuje, doprowadzając nieroztropnego gracza zamiast do maksymalnej wygranej, do możliwie największej przegranej. Aby tego uniknąć należy prześledzić każdą z dostępnych strategii pod kątem wartości przegranych i znaleźć taką strategię, po której zastosowaniu możliwa przegrana jest najmniejszą z możliwych.

Zastosowania

Teorię gier wykorzystuje się w wielu różnych dziedzinach, np. psychologii, socjologii, ekonomii oraz polityce. W ekonomii teorii używa się do analizy m.in.: relacji pomiędzy przedsiębiorstwami w oligopolu, duopolu, konkurencji doskonałej; polityki handlowej; konfliktów na rynku.

Równowaga Nasha

W grze niekooperacyjnej jest to stan w którym (Woźniak A. 2013, s.92 i 97):

• optymalne strategie jednego gracza są znane pozostałym,
• zmiana strategii nie powoduje poprawy sytuacji danego gracza,
• strategie innych graczy pozostają niezmienne,

Natomiast w grach z użyciem strategii dominującej można zaobserwować następujące zachowania:

• jeżeli każdy gracz posiada swoją strategię dominującą, wówczas gra ma jedną równowagę Nasha.
• wynik gry zależy od kilku strategii dominujących

Bibliografia

• Haman J.(2014), Gry wokół nas. Socjolog i teoria gier, SCHOLAR, Warszawa
• Malawski M., Sosnowska H., Wieczorek A., (2011), "Konkurencja i kooperacja - Teoria gier w ekonomii i naukach społecznych", Wydawnictwo Naukowe PWN, Warszawa
• Płatkowski T. (2012),Wstęp do teorii gier, Uniwersytet Warszawski
• Samuelson P. A., Nordhaus W. D. (2004),"Ekonomia. Tom 1", Wydawnictwo Naukowe PWN, Warszawa, s. 296-297, 332-345
• Straffin P. D. (2001), "Teoria gier" Wydawnictwo Naukowe SCHOLAR, Warszawa
• Varian H.R. (1997), "Mikroekonomia" Wydawnictwo Naukowe PWN, Warszawa, s. 498
• Watson J.(2011), Strategia.Wprowadzenie do teorii gier, Wolters, Warszawa
• Woźniak A. (2013), Decyzje w warunkach współzawodnictwa, CeDeWu, Warszawa

Autor: Katarzyna Sałagan, Magdalena Wiatrowska, Karolina Lisowska