Błąd bezwzględny: Różnice pomiędzy wersjami
m (cleanup bibliografii i rotten links) |
m (→Bibliografia: Clean up) |
||
| Linia 117: | Linia 117: | ||
* Zięba A. (2001) ''Natura rachunku niepewności pomiaru a jego nowa kodyfikacja.'' Postępy Fizyki, tom 52, zeszyt 5, Polskie Towarzystwo Fizyczne, Warszawa | * Zięba A. (2001) ''Natura rachunku niepewności pomiaru a jego nowa kodyfikacja.'' Postępy Fizyki, tom 52, zeszyt 5, Polskie Towarzystwo Fizyczne, Warszawa | ||
</noautolinks> | </noautolinks> | ||
[[Kategoria: | [[Kategoria:Miary statystyczne]] | ||
{{a|Katarzyna Kolano}} | {{a|Katarzyna Kolano}} | ||
{{#metamaster:description|Błąd bezwzględny to różnica między wynikiem pomiaru a wartością poprawną. Dowiedz się, jak obliczyć i interpretować tę wartość.}} | {{#metamaster:description|Błąd bezwzględny to różnica między wynikiem pomiaru a wartością poprawną. Dowiedz się, jak obliczyć i interpretować tę wartość.}} | ||
Wersja z 07:55, 8 lis 2023
| Błąd bezwzględny |
|---|
| Polecane artykuły |
Błąd bezwzględny definiowany jest jako algebraiczna różnica pomiędzy wynikiem pomiaru a miarą poprawną wielkości mierzonej (L. Czopek 1994, s. 171).
Zależność tą można przedstawić za pomocą wzoru:
gdzie:
Wartość błędu bezwzględnego, będąca odchyleniem wyniku pomiaru od wartości rzeczywistej, zawsze podawana jest w tych samych jednostkach co mierzona wielkość. Niemniej jednak, wyznaczenie wartości błędu bezwzględnego nie jest podstawą do zinterpretowania wyniku pomiaru. Zakładając, że błąd bezwzględny wynosi ΔX=±5mm to dokładność pomiaru można określić dopiero gdy znana jest wartość bezpośredniego odczytu x. Stąd, jeśli x wynosi 4 cm to błąd ΔX=±5mm jest duży i znaczący. Z kolei gdy x równe jest 1 km to błąd ten jest znikomy. Mając na uwadze powyższe rozważania należy pamiętać, aby zawsze obok wartości otrzymanej napisać zmierzony błąd: x±ΔX=(40±5) mm. Dopiero taki zapis, pozwalający na ocenę dokładności pomiaru jest wartościowy (H. Szydłowski 1973, s. 40-41)
TL;DR
Błąd bezwzględny to różnica pomiędzy wynikiem pomiaru a wartością rzeczywistą. Może być podzielony na błędy systematyczne, grube i przypadkowe. Błąd bezwzględny jest wykorzystywany w matematyce, ekonomii i metrologii. Jest różny od błędu względnego, który odzwierciedla jakość zjawiska. Błąd bezwzględny jest ważny do określenia dokładności pomiaru.
Podział błędów
Błędy ze względu na ich wpływ na wynik pomiaru dzielimy na: systematyczne, grube i przypadkowe (H. Szydłowski 1973, s. 39)
- Błędy systematyczne to takie, które w sposób niezmienny wpływają na wyniki pomiarów, wykonanych za pomocą tej samej techniki oraz tej samej aparatury pomiarowej. Mogą wynikać np. z niedokładności przyrządów pomiarowych czy też błędnej metody pomiaru (A. Zięba 2001, s. 243).
- Błędy grube charakteryzują się tym, że znacząco odbiegają od pozostałych pomiarów i należy je od razu wyeliminować i/lub powtórzyć pomiar. Ich źródłem może być błędnie odczytany lub zapisany wynik.
- Błędami przypadkowymi nazywa się błędy o charakterze losowym, nieprzewidywalnym. Z tego powodu bardzo ciężko je zidentyfikować i wyeliminować (H. Szydłowski 1973, s. 39-40).
Innym podziałem błędów, ze względu na ich pochodzenie są:
- błąd przyrządu pomiarowego,
- błąd metody pomiarowej,
- błąd wynikający z niedokładności zmysłów czy statystycznym charakterem zjawiska.
Ze względu na sposób zapisu rozróżnia się błędy bezwzględne, względne oraz procentowe.
Błąd bezwzględny w matematyce
"Niech a będzie przybliżeniem liczby x. Błąd bezwzględny przybliżenia jest to wartość bezwzględna różnicy między liczbą x i jej przybliżeniem a, czyli liczba |x-a|". (W. Babiański 2009, s. 78)
Dokonując algebraicznej interpretacji powyższej definicji otrzymano:
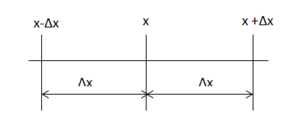
Błąd bezwzględny można także przedstawić za pomocą graficznej ilustracji (Rys. 1.)
Wartość błędu bezwzględnego w aspekcie matematycznym zawsze jest wartością nieujemną.
Przykład 1.
Śnieżka, będąca najwyższym szczytem Sudet, po raz pierwszy została zmierzona XVI wieku. Jej wysokość oszacowano na 5,5 km. Jednakże, pierwotną wysokość zweryfikowano i ostatecznie stwierdzono, że wysokość Śnieżki nie jest aż tak imponująca i wynosi 1,603 km. Obliczyć błąd bezwzględny.
Rozwiązanie:
a - 5,5 [km] przybliżona wartość
x - 1,602 [km] rzeczywista wartość
Δ=|x-a|=|1,602-5,5|= |-3,898|= 3,898 km
Otrzymany wynik należy zapisać: 1,602 ± 3,898 km
Błąd bezwzględny w ekonomii
Jednym z narzędzi analizy ekonomiczno - finansowej firmy, wykorzystywanym do wstępnej analizy kosztów jest ustalenie odchyleń kosztów rzeczywistych w stosunku do przyjętej bazy odniesienia. Odchylenia te dzielą się na odchylenia bezwzględne i względne.
Odchylenie bezwzględne (ΔKb) można wyznaczyć, korzystając ze wzoru:
Wyraża on bezwzględną kwotę kosztów, będących wynikiem różnicy między kosztami okresu badanego (Kb) a kosztami okresu bazowego (Ko). Wartość odchylenia bezwzględnego może być dodatnia lub ujemna. Odchylenie dodatnie wskazuje na wzrost kosztów, odchylenie ujemne natomiast mówi o tym, że wielkość kosztów w okresie badanym była mniejsza niż kosztów przyjętego okresu bazowego. Na tej podstawie można założyć że nastąpiło zjawisko bezwzględnej obniżki kosztów (Leszczyński Z. 2000, s. 238).
Błąd bezwzględny w metrologii
Każdy wynik pomiaru dowolnej wielkości fizycznej różni się od wartości rzeczywistej, ponieważ obarczony jest błędem pomiarowym. Przyczyną występowania tych błędów jest skończona dokładność przyrządów pomiarowych (woltomierz, amperomierz, linijka itp.) przy pomocy których dokonywany jest pomiar. Na wartość błędu pomiarowego przyrządu analogowego wpływa jego klasa dokładności (K) oraz zakres pomiarowy (Z). Wskaźnik klasy dokładności miernika analogowego rozumiany jest jako liczbę, wyrażająca procentowy stosunek wartości bezwzględnego błędu granicznego Δx do wartości zakresu pomiarowego:
Na podstawie podanej zależności, można wywnioskować, że "bezwzględny błąd pomiaru miernika w warunkach odniesienia, wyrażony w procentach wartości zakresu, dla żadnej wartości wielkości mierzonej w zakresie pomiarowym nie powinien przekraczać wskaźnika klasy dokładności. Dla przyrządów wskazówkowych rozróżnia się kilka klas dokładności, a najczęściej spotykane to: 0,2; 0,5; 1; 1,5; 2,5; przy czym im większy wskaźnik klasy dokładności tym większy błąd pomiaru. Przekształcając powyższy wzór, uzyskujemy zależność na obliczenie bezwzględnego błędu granicznego:
(…) Bezwzględny błąd graniczny pomiaru miernikiem analogowym jest stały w całym zakresie pomiarowym i zależy od klasy przyrządu i zakresu pomiarowego" (Burnos P. 2010, s. 4-5).
Przykład 2.
Przy pomocy watomierza klasy 1 dla zakresu prądowego 0,5 A i napięciowego 100 V zmierzono moc żarówki, uzyskując pomiar P = 45,3 W. Obliczyć błąd bezwględny pomiaru mocy.
Rozwiązanie:
Zatem błąd bezwzględny pomiaru wynosi 0,5 W. Tym samym, moc żarówki możemy zapisać następująco: P = (45,3 ± 0,5) W.
Różnica między błędem bezwzględnym a względnym
Błąd bezwzględny, w przeciwieństwie do błędu względnego, nie odzwierciedla jakości zjawiska, lecz informuje nas wyłącznie o wielkości odchylenia od wartości rzeczywistej (Fiałkowska M. 2009, s. 338-339). Wyznaczenie błędu bezwzględnego nie pozwala na ocenę badanego zjawiska. Aby wyciągnąć wnioski z analizowanego zjawiska, należy wyznaczyć błąd względny.
Bibliografia
- Babiański W. (2009) Matematyka 1. Podręcznik dla liceum ogólnokształcącego, liceum profilowanego i technikum. Nowa Era, Warszawa
- Burnos P. (2010) Laboratorium metrologii AGH. Analiza błędów i niepewności wyników pomiarowych. AGH, Kraków
- Fiałkowska M., Fiałkowski K., Saganowska B. (2009) Fizyka dla szkół ponadgimnazjalnych. ZamKor, Kraków
- Fogra (1995), Popularna Encyklopedia Powszechna, Wydawnictwo Oficyna Wydawnicza Fogra, Kraków
- Leszczyński Z., Skowronek-Mielczarek A. (2000) Analiza ekonomiczno - finansowa firmy. Diffin, Warszawa
- Szydłowski H. (1973) Pracownia fizyczna. PWN, Warszawa
- Zięba A. (2001) Natura rachunku niepewności pomiaru a jego nowa kodyfikacja. Postępy Fizyki, tom 52, zeszyt 5, Polskie Towarzystwo Fizyczne, Warszawa
Autor: Katarzyna Kolano