CPM: Różnice pomiędzy wersjami
m (Dodanie MetaData Description) |
m (cleanup bibliografii i rotten links) |
||
| (Nie pokazano 13 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
'''CPM''' (''[[metoda]] ścieżki krytycznej, z ang. Critical Path Method'') należy do grupy deterministycznych technik planowania sieciowego. Jej podstawę stanowi budowa szczególnego rodzaju grafu sieciowego (przedstawiającego czynności i zdarzenia składające się na [[projekt]]) i dokonywanie wyliczeń na podstawie tego grafu. Dzięki tym wyliczeniem uzyskujemy [[plan]] realizacji projektu. Ten specyficzny rodzaj grafu (sieci) jest określany siecią zależności lub wykresem sieciowym. Sieć ta opiera się na dwupunktowych modelach sieciowych, czyli takich gdzie czynności są reprezentowane za pomocą łuków grafu, a zdarzenia za pomocą węzłów grafu [M. Trocki i in. 2003, s. 161-162]. Metodę ścieżki krytycznej wykorzystuje się do planowania i kontroli projektów, gdzie znana jest [[technologia]] i powiązania organizacyjne. Do takich projektów można zaliczyć [[inwestycje]] budowlane, remontowe, projekty związane z produkcję jednostkową skomplikowanych wyrobów (np. samolotów). | |||
'''CPM''' (''[[metoda]] ścieżki krytycznej, z ang. Critical Path Method'') należy do grupy deterministycznych technik planowania sieciowego. Jej podstawę stanowi budowa szczególnego rodzaju grafu sieciowego (przedstawiającego czynności i zdarzenia składające się na [[projekt]]) i dokonywanie wyliczeń na podstawie tego grafu. Dzięki tym wyliczeniem uzyskujemy [[plan]] realizacji projektu. Ten specyficzny rodzaj grafu (sieci) jest określany siecią zależności lub wykresem sieciowym. Sieć ta opiera się na dwupunktowych modelach sieciowych, czyli takich gdzie czynności są reprezentowane za pomocą łuków grafu, a zdarzenia za pomocą węzłów grafu [M. Trocki i in. 2003, s. 161-162]. Metodę ścieżki krytycznej wykorzystuje się do planowania i kontroli projektów, gdzie znana jest [[technologia]] i powiązania organizacyjne. Do takich projektów można zaliczyć [[inwestycje]] budowlane, remontowe, projekty związane z produkcję jednostkową skomplikowanych wyrobów (np. samolotów). | |||
==TL;DR== | ==TL;DR== | ||
| Linia 23: | Linia 6: | ||
==Geneza CPM== | ==Geneza CPM== | ||
Metodę CPM opracowano w latach 1956-1957 w USA. Jej autorami byli J. Kelley i R. Walker, pracownicy firmy DuPont. Opracowali tą metodę w celu usprawnienia prac przy produkcji neopranu. Inżynierowie byli zaniepokojeni dużą ilością przestojów podczas konserwacji maszyn. Dzięki zastosowaniu metody CPM mogli skrócić czas przestojów ze 125 do 93 godzin, dzięki temu mogli poprawić wyniki ekonomiczne. Metoda ta stanowi graficzne przedstawienie, zorganizowanego działania, które zmierza do realizacji wyznaczonego celu w określonym czasie, przy określonych zasobach i budżecie. Na [[przedsięwzięcie]] składa się skończona liczba wzajemnie ze sobą powiązanych i wykonanych w odpowiedniej kolejności czynności (znane są czasy ich trwania) [A. Grześ 2014, s. 207]. | Metodę CPM opracowano w latach 1956-1957 w USA. Jej autorami byli J. Kelley i R. Walker, pracownicy firmy DuPont. Opracowali tą metodę w celu usprawnienia prac przy produkcji neopranu. Inżynierowie byli zaniepokojeni dużą ilością przestojów podczas konserwacji maszyn. Dzięki zastosowaniu metody CPM mogli skrócić czas przestojów ze 125 do 93 godzin, dzięki temu mogli poprawić wyniki ekonomiczne. Metoda ta stanowi graficzne przedstawienie, zorganizowanego działania, które zmierza do realizacji wyznaczonego celu w określonym czasie, przy określonych zasobach i budżecie. Na [[przedsięwzięcie]] składa się skończona liczba wzajemnie ze sobą powiązanych i wykonanych w odpowiedniej kolejności czynności (znane są czasy ich trwania) [A. Grześ 2014, s. 207]. | ||
==Algorytm metody CPM== | ==Algorytm metody CPM== | ||
1. Obliczenie czasów najwcześniejszych możliwych terminów rozpoczęcia czynności (obliczeń dokonujemy idąc w przód wykresu). ''Uwaga'': W metodzie CPM zakłada się, że czasy trwania poszczególnych czynności są dokładnie znane (deterministyczne). | 1. Obliczenie czasów najwcześniejszych możliwych terminów rozpoczęcia czynności (obliczeń dokonujemy idąc w przód wykresu). ''Uwaga'': W metodzie CPM zakłada się, że czasy trwania poszczególnych czynności są dokładnie znane (deterministyczne). | ||
* Przyjmij najwcześniejszy możliwy termin zdarzenia początkowego (pierwszego z lewej) równy 0. | * Przyjmij najwcześniejszy możliwy termin zdarzenia początkowego (pierwszego z lewej) równy 0. | ||
| Linia 37: | Linia 17: | ||
* Oblicz najpóźniejszy dopuszczalny termin zaistnienia poszczególnych zdarzeń, rozpoczynając od zdarzeń najbliższych zdarzeniu końcowemu (najpóźniejszy dopuszczalny termin zaistnienia - czas trwania czynności prowadzącej do tego zdarzenia (''Uwaga'': gdy jakieś [[zdarzenie]] jest początkiem dwóch lub więcej czynności, najpóźniejszy dopuszczalny moment zaistnienia zdarzenia będzie równy minimum odpowiednich różnic). | * Oblicz najpóźniejszy dopuszczalny termin zaistnienia poszczególnych zdarzeń, rozpoczynając od zdarzeń najbliższych zdarzeniu końcowemu (najpóźniejszy dopuszczalny termin zaistnienia - czas trwania czynności prowadzącej do tego zdarzenia (''Uwaga'': gdy jakieś [[zdarzenie]] jest początkiem dwóch lub więcej czynności, najpóźniejszy dopuszczalny moment zaistnienia zdarzenia będzie równy minimum odpowiednich różnic). | ||
[[File:Ilustracja konwencji oznaczeń.jpg|thumb| Rys. 1. Ilustracja konwencji oznaczeń]] | [[File:Ilustracja konwencji oznaczeń.jpg|thumb| Rys. 1. Ilustracja konwencji oznaczeń]] | ||
* Powtórz opisane kroki dla wszystkich zadań. | * Powtórz opisane kroki dla wszystkich zadań. | ||
| Linia 45: | Linia 25: | ||
4. Wyznaczenie ścieżki krytycznej - czynności znajdujące się na tej drodze mają zerowy zapas czasu. | 4. Wyznaczenie ścieżki krytycznej - czynności znajdujące się na tej drodze mają zerowy zapas czasu. | ||
<google>n</google> | |||
==Wyznaczenie ścieżki krytycznej== | ==Wyznaczenie ścieżki krytycznej== | ||
[[File:Struktura przedsięwzięcia wraz z czasami realizacji poszczególnych operacji (czynności).jpg|thumb| Rys. 2. Struktura przedsięwzięcia wraz z czasami realizacji poszczególnych operacji (czynności)]] | |||
Ścieżka krytyczna jest najdłużej trwającym ze wszystkich możliwych ciągów chronologicznie ułożonych zadań takich, że każde następne nie może się rozpocząć, dopóki poprzednie się nie skończy. W technice ścieżki krytycznej znany jest termin rozpoczęcia i zakończenia projektu, kolejność poszczególnych zdarzeń i wzajemne powiązania między nimi. Znane są też czasy trwania czynności, które muszą zostać zrealizowane, aby mogły zaistnieć określone zdarzenia. Zdarzenie nie może wystąpić, do czasu gdy wszystkie czynności dotyczące go nie zostały zakończone. Kolejność poszczególnych zdarzeń oraz wykonanych między nimi czynności określa technologia i powiązania organizacyjne. | Ścieżka krytyczna jest najdłużej trwającym ze wszystkich możliwych ciągów chronologicznie ułożonych zadań takich, że każde następne nie może się rozpocząć, dopóki poprzednie się nie skończy. W technice ścieżki krytycznej znany jest termin rozpoczęcia i zakończenia projektu, kolejność poszczególnych zdarzeń i wzajemne powiązania między nimi. Znane są też czasy trwania czynności, które muszą zostać zrealizowane, aby mogły zaistnieć określone zdarzenia. Zdarzenie nie może wystąpić, do czasu gdy wszystkie czynności dotyczące go nie zostały zakończone. Kolejność poszczególnych zdarzeń oraz wykonanych między nimi czynności określa technologia i powiązania organizacyjne. | ||
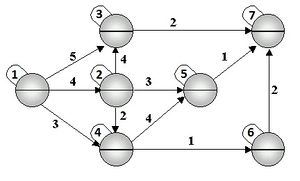
'''Załóżmy, że mamy dany graf (rys. 2), przy pomocy którego zapisaliśmy strukturę naszego przedsięwzięcia wraz z czasami realizacji poszczególnych operacji (czynności).''' | '''Załóżmy, że mamy dany graf (rys. 2), przy pomocy którego zapisaliśmy strukturę naszego przedsięwzięcia wraz z czasami realizacji poszczególnych operacji (czynności).''' | ||
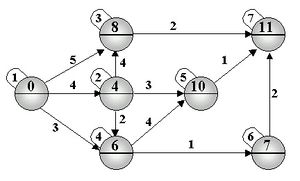
Pierwszym krokiem przy wyznaczaniu ścieżki krytycznej jest określenie dla każdego zdarzenia najwcześniejszego możliwego momentu zaistnienia. Przy wyznaczaniu ścieżki krytycznej przyjmuje się, że najwcześniejszy możliwy moment zaistnienia zdarzenia początkowego numer 1 wynosi 0. Najwcześniejszy możliwy moment zdążenia następnego (np. 2) jest równy sumie najwcześniejszego możliwego momentu zaistnienia zdarzenia 1 oraz długości czasu trwania czynności prowadzącej do zdarzenia 2 (zdarzenie 2 zajdzie po 4 jednostkach czasu). Przechodząc od początku do końca wykresu, wyznacza się kolejno najwcześniejsze momenty powstałych zdarzeń (rys. 3) | Pierwszym krokiem przy wyznaczaniu ścieżki krytycznej jest określenie dla każdego zdarzenia najwcześniejszego możliwego momentu zaistnienia. Przy wyznaczaniu ścieżki krytycznej przyjmuje się, że najwcześniejszy możliwy moment zaistnienia zdarzenia początkowego numer 1 wynosi 0. Najwcześniejszy możliwy moment zdążenia następnego (np. 2) jest równy sumie najwcześniejszego możliwego momentu zaistnienia zdarzenia 1 oraz długości czasu trwania czynności prowadzącej do zdarzenia 2 (zdarzenie 2 zajdzie po 4 jednostkach czasu). Przechodząc od początku do końca wykresu, wyznacza się kolejno najwcześniejsze momenty powstałych zdarzeń (rys. 3) | ||
| Linia 66: | Linia 47: | ||
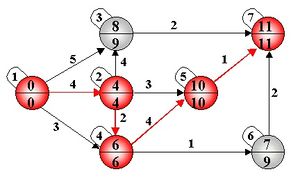
[[File:Wyznaczenie ścieżki krytycznej.jpg|thumb| Rys. 5 Wyznaczenie ścieżki krytycznej]] | [[File:Wyznaczenie ścieżki krytycznej.jpg|thumb| Rys. 5 Wyznaczenie ścieżki krytycznej]] | ||
W rozpatrywanym przypadku ścieżka krytyczna przechodzi przez zdarzenia 1-2-4-5-7 (na rysunku 5 zaznaczono ją kolorem czerwonym). Długość ścieżki krytycznej wynosi 11 jednostek (czasu). [[Kierownik]] projektu powinien szczególnie zwrócić uwagę na zdarzenia leżące ta tej ścieżce. Opóźnienie jednego zdarzenia spowoduje przesunięcie wyznaczonego terminu zakończenia projektu. | W rozpatrywanym przypadku ścieżka krytyczna przechodzi przez zdarzenia 1-2-4-5-7 (na rysunku 5 zaznaczono ją kolorem czerwonym). Długość ścieżki krytycznej wynosi 11 jednostek (czasu). [[Kierownik]] projektu powinien szczególnie zwrócić uwagę na zdarzenia leżące ta tej ścieżce. Opóźnienie jednego zdarzenia spowoduje przesunięcie wyznaczonego terminu zakończenia projektu. | ||
Należy zwrócić uwagę, że nie zawsze czynności, które łączą zdarzenia krytyczne muszą być czynnościami krytycznymi !!! Jak widać na rysunku 5 czynność (1-4) łączy zdarzenia krytyczne, lecz sama nie jest czynnością krytyczną. Opóźnienie przy wykonaniu tej czynności nie musi pociągać za sobą opóźnienia w wykonaniu całego przedsięwzięcia. | Należy zwrócić uwagę, że nie zawsze czynności, które łączą zdarzenia krytyczne muszą być czynnościami krytycznymi !!! Jak widać na rysunku 5 czynność (1-4) łączy zdarzenia krytyczne, lecz sama nie jest czynnością krytyczną. Opóźnienie przy wykonaniu tej czynności nie musi pociągać za sobą opóźnienia w wykonaniu całego przedsięwzięcia. | ||
{{infobox5|list1={{i5link|a=[[MPM]]}} — {{i5link|a=[[Wykresy sieciowe]]}} — {{i5link|a=[[Planowanie ścieżki krytycznej]]}} — {{i5link|a=[[Cyklogram]]}} — {{i5link|a=[[Estymacja czasu trwania zadań]]}} — {{i5link|a=[[GERT]]}} — {{i5link|a=[[Metoda łańcucha krytycznego]]}} — {{i5link|a=[[PERT]]}} — {{i5link|a=[[Notacja AoA]]}} }} | |||
==Bibliografia== | ==Bibliografia== | ||
* Błaszczyk T., Nowak M. (2010) | <noautolinks> | ||
* Brandenburg H.(2011) | * Błaszczyk T., Nowak M. (2010), ''Wielokryterialne wspomaganie decyzji w harmonogramowaniu projektów'', Decyzje, nr 13 | ||
* Dźwigoł H. (2016) | * Brandenburg H. (2011), ''Zarządzanie lokalnymi projektami rozwojowymi'', Wydawnictwo Akademii Ekonomicznej, Katowice | ||
* Grześ A. (2014) | * Dźwigoł H. (2016), ''Analiza wybranych metod w procesie badawczym'', Marketing i Rynek, nr 7 | ||
* Kisielnicki J. ( | * Grześ A. (2014), ''[https://repozytorium.uwb.edu.pl/jspui/bitstream/11320/2997/1/14_Grzes.pdf Wykres Gantta a metoda ścieżki krytycznej (CPM)]'', Czasopismo Optimum. Studia Ekonomiczne, Nr 4 (70) | ||
* Połoński M. (2005) | * Kisielnicki J. (2017), ''Zarządzanie projektami. Ludzie - procedury - wyniki'', Wydawnictwo Nieoczywiste, Piaseczno | ||
* Trocki M. | * Połoński M. (2005), ''Rozkład czasu trwania czynności a termin zakończenia przedsięwzięcia z uwzględnieniem elementów analizy ryzyka'', ACTA Scientiarum Polonorum. Archtectura, 4(2) | ||
* Wrycza S. (2010) | * Trocki M., Grucza B., Ogonek K. (2003), ''Zarządzanie projektami'', PWE, Warszawa | ||
* Wrycza S. (red.) (2010), ''Informatyka ekonomiczna. Podręcznik akademicki'', Polskie Wydawnictwo Ekonomiczne, Warszawa | |||
</noautolinks> | |||
{{a|Paweł Woźniak}} | {{a|Paweł Woźniak}} | ||
[[Kategoria:Harmonogramowanie]] | |||
[[Kategoria: | |||
{{#metamaster:description|CPM to deterministyczna technika planowania sieciowego oparta na grafie sieciowym. Wykorzystywana w projektach inwestycyjnych i produkcji.}} | {{#metamaster:description|CPM to deterministyczna technika planowania sieciowego oparta na grafie sieciowym. Wykorzystywana w projektach inwestycyjnych i produkcji.}} | ||
Aktualna wersja na dzień 23:33, 10 sty 2024
CPM (metoda ścieżki krytycznej, z ang. Critical Path Method) należy do grupy deterministycznych technik planowania sieciowego. Jej podstawę stanowi budowa szczególnego rodzaju grafu sieciowego (przedstawiającego czynności i zdarzenia składające się na projekt) i dokonywanie wyliczeń na podstawie tego grafu. Dzięki tym wyliczeniem uzyskujemy plan realizacji projektu. Ten specyficzny rodzaj grafu (sieci) jest określany siecią zależności lub wykresem sieciowym. Sieć ta opiera się na dwupunktowych modelach sieciowych, czyli takich gdzie czynności są reprezentowane za pomocą łuków grafu, a zdarzenia za pomocą węzłów grafu [M. Trocki i in. 2003, s. 161-162]. Metodę ścieżki krytycznej wykorzystuje się do planowania i kontroli projektów, gdzie znana jest technologia i powiązania organizacyjne. Do takich projektów można zaliczyć inwestycje budowlane, remontowe, projekty związane z produkcję jednostkową skomplikowanych wyrobów (np. samolotów).
TL;DR
Metoda CPM jest techniką planowania sieciowego, która opiera się na budowie grafu sieciowego i wyliczeniach na podstawie tego grafu. Metoda ta służy do planowania i kontroli projektów, gdzie znana jest technologia i powiązania organizacyjne. Polega na obliczaniu najwcześniejszych i najpóźniejszych możliwych terminów rozpoczęcia i zakończenia poszczególnych zadań oraz wyznaczaniu ścieżki krytycznej - najdłużej trwającego ciągu zadań, który determinuje czas trwania całego projektu.
Geneza CPM
Metodę CPM opracowano w latach 1956-1957 w USA. Jej autorami byli J. Kelley i R. Walker, pracownicy firmy DuPont. Opracowali tą metodę w celu usprawnienia prac przy produkcji neopranu. Inżynierowie byli zaniepokojeni dużą ilością przestojów podczas konserwacji maszyn. Dzięki zastosowaniu metody CPM mogli skrócić czas przestojów ze 125 do 93 godzin, dzięki temu mogli poprawić wyniki ekonomiczne. Metoda ta stanowi graficzne przedstawienie, zorganizowanego działania, które zmierza do realizacji wyznaczonego celu w określonym czasie, przy określonych zasobach i budżecie. Na przedsięwzięcie składa się skończona liczba wzajemnie ze sobą powiązanych i wykonanych w odpowiedniej kolejności czynności (znane są czasy ich trwania) [A. Grześ 2014, s. 207].
Algorytm metody CPM
1. Obliczenie czasów najwcześniejszych możliwych terminów rozpoczęcia czynności (obliczeń dokonujemy idąc w przód wykresu). Uwaga: W metodzie CPM zakłada się, że czasy trwania poszczególnych czynności są dokładnie znane (deterministyczne).
- Przyjmij najwcześniejszy możliwy termin zdarzenia początkowego (pierwszego z lewej) równy 0.
- Oblicz najwcześniejszy możliwy termin rozpoczęcia następnego zadania jako najwcześniejszy możliwy termin zaistnienia zdarzenia poprzedniego + czas trwania czynności prowadzącej do tego zdarzenia (Uwaga:jeśli jest więcej poprzedników, do obliczeń weź zadanie o najpóźniejszym czasie zaistnienia).
- Powtórz opisane kroki dla wszystkich zadań.
2. Obliczenie najpóźniejszych dopuszczalnych terminów zaistnienia poszczególnych zdarzeń (obliczeń dokonujemy idąc wstecz wykresu).
- Zdarzeniu końcowemu (ostatniemu z prawej) należy przypisać najpóźniejszy dopuszczalny termin zaistnienia, który jest równy najwcześniejszemu możliwemu terminowi zaistnienia.
- Oblicz najpóźniejszy dopuszczalny termin zaistnienia poszczególnych zdarzeń, rozpoczynając od zdarzeń najbliższych zdarzeniu końcowemu (najpóźniejszy dopuszczalny termin zaistnienia - czas trwania czynności prowadzącej do tego zdarzenia (Uwaga: gdy jakieś zdarzenie jest początkiem dwóch lub więcej czynności, najpóźniejszy dopuszczalny moment zaistnienia zdarzenia będzie równy minimum odpowiednich różnic).
- Powtórz opisane kroki dla wszystkich zadań.
3. Obliczenie zapasów czasu.
- Zapas = najpóźniejszy dopuszczalny termin - najwcześniejszy możliwy termin.
- Powtórz opisane kroki dla wszystkich zadań.
4. Wyznaczenie ścieżki krytycznej - czynności znajdujące się na tej drodze mają zerowy zapas czasu.
Wyznaczenie ścieżki krytycznej
Ścieżka krytyczna jest najdłużej trwającym ze wszystkich możliwych ciągów chronologicznie ułożonych zadań takich, że każde następne nie może się rozpocząć, dopóki poprzednie się nie skończy. W technice ścieżki krytycznej znany jest termin rozpoczęcia i zakończenia projektu, kolejność poszczególnych zdarzeń i wzajemne powiązania między nimi. Znane są też czasy trwania czynności, które muszą zostać zrealizowane, aby mogły zaistnieć określone zdarzenia. Zdarzenie nie może wystąpić, do czasu gdy wszystkie czynności dotyczące go nie zostały zakończone. Kolejność poszczególnych zdarzeń oraz wykonanych między nimi czynności określa technologia i powiązania organizacyjne.
Załóżmy, że mamy dany graf (rys. 2), przy pomocy którego zapisaliśmy strukturę naszego przedsięwzięcia wraz z czasami realizacji poszczególnych operacji (czynności).
Pierwszym krokiem przy wyznaczaniu ścieżki krytycznej jest określenie dla każdego zdarzenia najwcześniejszego możliwego momentu zaistnienia. Przy wyznaczaniu ścieżki krytycznej przyjmuje się, że najwcześniejszy możliwy moment zaistnienia zdarzenia początkowego numer 1 wynosi 0. Najwcześniejszy możliwy moment zdążenia następnego (np. 2) jest równy sumie najwcześniejszego możliwego momentu zaistnienia zdarzenia 1 oraz długości czasu trwania czynności prowadzącej do zdarzenia 2 (zdarzenie 2 zajdzie po 4 jednostkach czasu). Przechodząc od początku do końca wykresu, wyznacza się kolejno najwcześniejsze momenty powstałych zdarzeń (rys. 3)
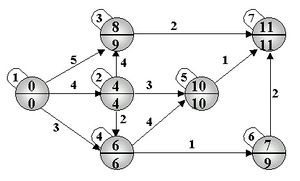
W następnym kroku obliczamy najpóźniejszy dopuszczalny moment zaistnienia poszczególnych zdarzeń, rozpoczynając od zdarzeń najbliższych zdarzeniu końcowemu, gdzie samemu zdarzeniu końcowemu należy przypisać najpóźniejszy dopuszczalny moment zaistnienia, który jest równy najwcześniejszemu możliwemu momentowi zaistnienia (zdarzenie 7). Przechodząc tym razem od końca do początku wykresu, wyznacza się kolejno najpóźniejsze momenty powstałych zdarzeń (rys. 4). Gdy jakieś zdarzenie jest początkiem dwóch lub więcej czynności, najpóźniejszy dopuszczalny moment zaistnienia zdarzenia będzie równy minimum odpowiednich różnic.
Najważniejszym i kończącym elementem tej metody jest wyznaczenie ścieżki krytycznej, którą definiujemy jako ciąg działań, dla którego suma czasów jest największa ze wszystkich możliwych dróg łączących zdarzenie końcowe ze zdarzeniem początkowym. Czynności znajdujące się na tej drodze mają zerowy zapas czasu (najpóźniejszy dopuszczalny termin - najwcześniejszy możliwy termin) [J. Kisielnicki 2011, s. 251].
W rozpatrywanym przypadku ścieżka krytyczna przechodzi przez zdarzenia 1-2-4-5-7 (na rysunku 5 zaznaczono ją kolorem czerwonym). Długość ścieżki krytycznej wynosi 11 jednostek (czasu). Kierownik projektu powinien szczególnie zwrócić uwagę na zdarzenia leżące ta tej ścieżce. Opóźnienie jednego zdarzenia spowoduje przesunięcie wyznaczonego terminu zakończenia projektu. Należy zwrócić uwagę, że nie zawsze czynności, które łączą zdarzenia krytyczne muszą być czynnościami krytycznymi !!! Jak widać na rysunku 5 czynność (1-4) łączy zdarzenia krytyczne, lecz sama nie jest czynnością krytyczną. Opóźnienie przy wykonaniu tej czynności nie musi pociągać za sobą opóźnienia w wykonaniu całego przedsięwzięcia.
| CPM — artykuły polecane |
| MPM — Wykresy sieciowe — Planowanie ścieżki krytycznej — Cyklogram — Estymacja czasu trwania zadań — GERT — Metoda łańcucha krytycznego — PERT — Notacja AoA |
Bibliografia
- Błaszczyk T., Nowak M. (2010), Wielokryterialne wspomaganie decyzji w harmonogramowaniu projektów, Decyzje, nr 13
- Brandenburg H. (2011), Zarządzanie lokalnymi projektami rozwojowymi, Wydawnictwo Akademii Ekonomicznej, Katowice
- Dźwigoł H. (2016), Analiza wybranych metod w procesie badawczym, Marketing i Rynek, nr 7
- Grześ A. (2014), Wykres Gantta a metoda ścieżki krytycznej (CPM), Czasopismo Optimum. Studia Ekonomiczne, Nr 4 (70)
- Kisielnicki J. (2017), Zarządzanie projektami. Ludzie - procedury - wyniki, Wydawnictwo Nieoczywiste, Piaseczno
- Połoński M. (2005), Rozkład czasu trwania czynności a termin zakończenia przedsięwzięcia z uwzględnieniem elementów analizy ryzyka, ACTA Scientiarum Polonorum. Archtectura, 4(2)
- Trocki M., Grucza B., Ogonek K. (2003), Zarządzanie projektami, PWE, Warszawa
- Wrycza S. (red.) (2010), Informatyka ekonomiczna. Podręcznik akademicki, Polskie Wydawnictwo Ekonomiczne, Warszawa
Autor: Paweł Woźniak