Model związków encji: Różnice pomiędzy wersjami
m (Infobox update) |
m (cleanup bibliografii i rotten links) |
||
| (Nie pokazano 16 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
'''Model związków encji''', określany jest również jako: [[model]] ER lub ERD. Skróty te pochodzą od angielskiej nazwy ''Entity Relationship Diagram''. [[Metoda]] zaprezentowana została po raz pierwszy przez Petera Chena w 1976 roku. Późniejszych, drobnych modyfikacji w diagramie dokonali między innymi Charles Bachman oraz James Martin. Jest to jedna z najpopularniejszych, dotychczas zaprojektowanych, metod [[modelowanie|modelowania]] danych. | '''Model związków encji''', określany jest również jako: [[model]] ER lub ERD. Skróty te pochodzą od angielskiej nazwy ''Entity Relationship Diagram''. [[Metoda]] zaprezentowana została po raz pierwszy przez Petera Chena w 1976 roku. Późniejszych, drobnych modyfikacji w diagramie dokonali między innymi Charles Bachman oraz James Martin. Jest to jedna z najpopularniejszych, dotychczas zaprojektowanych, metod [[modelowanie|modelowania]] danych. | ||
Diagramy te pokazują pewnego rodzaju obiekty, nazywane również encjami, których cechy charakterystyczne, czyli atrybuty, a także relacje jakie między nimi zachodzą, przechowywane są w [[system informacyjny|systemie informacyjnym]]. Warto zauważyć, że dla danego systemu tworzony jest jeden, spójny diagram. Nie przeprowadza się dekompozycji modelu na mniejsze części. Można dokonać jego podziału jedynie w sytuacji, kiedy dąży się do zaprezentowania i wydruku systemu. | Diagramy te pokazują pewnego rodzaju obiekty, nazywane również encjami, których cechy charakterystyczne, czyli atrybuty, a także relacje jakie między nimi zachodzą, przechowywane są w [[system informacyjny|systemie informacyjnym]]. Warto zauważyć, że dla danego systemu tworzony jest jeden, spójny diagram. Nie przeprowadza się dekompozycji modelu na mniejsze części. Można dokonać jego podziału jedynie w sytuacji, kiedy dąży się do zaprezentowania i wydruku systemu. | ||
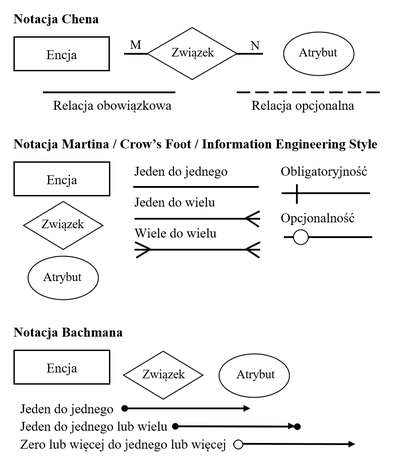
Należy zauważyć, że wyróżnić można różne notacje diagramów. Obecnie wśród najpopularniejszych wymienia się między innymi notację: Chena, Bachmana, Crow’s Foot, Martina, czy też Barkera. W zależności od stosowanej notacji, odmienne mogą być na przykład oznaczenia poszczególnych związków, ich liczebności, czy też opcjonalności, jakie występują w ERD (D. Olczyk 2010, s. 93; K. Sacha 2010, s. 86; K. Polańska 2015, s. 24 | Należy zauważyć, że wyróżnić można różne notacje diagramów. Obecnie wśród najpopularniejszych wymienia się między innymi notację: Chena, Bachmana, Crow’s Foot, Martina, czy też Barkera. W zależności od stosowanej notacji, odmienne mogą być na przykład oznaczenia poszczególnych związków, ich liczebności, czy też opcjonalności, jakie występują w ERD (D. Olczyk 2010, s. 93; K. Sacha 2010, s. 86; K. Polańska 2015, s. 24-25; S. Wrycza i in. 2019, s. 379). | ||
==TL;DR== | |||
Model związków encji (ER lub ERD) to metoda modelowania danych, która opisuje obiekty (encje), ich cechy (atrybuty) oraz relacje między nimi. Encje są przedstawiane jako prostokąty, a atrybuty jako owale. Związki są reprezentowane przez strzałki lub linie przerywane. Istnieją różne notacje ER, które różnią się oznaczeniami związków i atrybutów. W zależności od notacji, związki mogą mieć różne typy (jeden do jednego, jeden do wielu, wiele do wielu) i opcjonalność. Model ER jest używany do projektowania baz danych i systemów informacyjnych. | |||
==Elementy modelu== | ==Elementy modelu== | ||
W skład modelu związków encji wchodzą elementy takie jak: | W skład modelu związków encji wchodzą elementy takie jak: '''encja''', '''atrybut''', '''związek'''. | ||
===Encja=== | ===Encja=== | ||
'''Encja''' (ang. ''entity'') wyraża różnego rodzaju obiekty, składniki rzeczywistości, czy też szeroko pojęty byt. W diagramie prezentowana jest najczęściej w formie prostokąta o ostrych, bądź zaokrąglonych rogach. Nazwa danej encji umiejscowiona jest zazwyczaj w pierwszym wersie, a dodatkowo oznaczana jest innym kolorem, bądź też rodzajem czcionki | '''Encja''' (ang. ''entity'') wyraża różnego rodzaju obiekty, składniki rzeczywistości, czy też szeroko pojęty byt. W diagramie prezentowana jest najczęściej w formie prostokąta o ostrych, bądź zaokrąglonych rogach. Nazwa danej encji umiejscowiona jest zazwyczaj w pierwszym wersie, a dodatkowo oznaczana jest innym kolorem, bądź też rodzajem czcionki - tak, aby łatwo było ją dostrzec. Nazwą jest rzeczownik, który w przypadku jednej encji jest w liczbie pojedynczej, natomiast w przypadku magazynu danych jest w liczbie mnogiej. Przykładami pojedynczych obiektów mogą być: przedmiot, pojazd, osoba, książka, zamówienie, jak i również pojęcie. Natomiast magazynami danych nazwać można na przykład osoby, zdarzenia, faktury, zamówienia, itd.. | ||
Dwie podstawowe własności encji: | Dwie podstawowe własności encji: | ||
| Linia 30: | Linia 19: | ||
Z tego też powodu, warto rozróżnić pojęcie '''encji''' / '''typu encji''' od '''wystąpienia''' / '''instancji encji'''. Konkretne obiekty, jakie pojawiają się w świecie, są określane mianem instancji. Przykładowo: encją będzie ''Uniwersytet'', zaś jej instancją będzie jeden konkretny na przykład ''Uniwersytet Ekonomiczny w Krakowie'' (D. Olczyk 2010, s. 93; K. Sacha 2010, s. 85; J. Kisielnicki 2013, s. 130; K. Polańska 2015, s. 25; S. Wrycza i in. 2019, s. 379). | Z tego też powodu, warto rozróżnić pojęcie '''encji''' / '''typu encji''' od '''wystąpienia''' / '''instancji encji'''. Konkretne obiekty, jakie pojawiają się w świecie, są określane mianem instancji. Przykładowo: encją będzie ''Uniwersytet'', zaś jej instancją będzie jeden konkretny na przykład ''Uniwersytet Ekonomiczny w Krakowie'' (D. Olczyk 2010, s. 93; K. Sacha 2010, s. 85; J. Kisielnicki 2013, s. 130; K. Polańska 2015, s. 25; S. Wrycza i in. 2019, s. 379). | ||
<google>n</google> | |||
===Atrybut=== | ===Atrybut=== | ||
'''Atrybut''' (ang. ''attribute'') to pewnego rodzaju cechy charakterystyczne dla danej encji, które są przechowywane w danym [[system|systemie]]. Jej zadaniem jest opisywanie, czy też określanie danego bytu. Każdy poszczególny obiekt musi zostać opisany przez minimum jeden atrybut, choć często jest to pewien ich zbiór. W diagramie prezentowane mogą być między innymi jako owal. | '''Atrybut''' (ang. ''attribute'') to pewnego rodzaju cechy charakterystyczne dla danej encji, które są przechowywane w danym [[system|systemie]]. Jej zadaniem jest opisywanie, czy też określanie danego bytu. Każdy poszczególny obiekt musi zostać opisany przez minimum jeden atrybut, choć często jest to pewien ich zbiór. W diagramie prezentowane mogą być między innymi jako owal. | ||
Pojedynczy byt musi mieć również wyraźnie określony tzw. '''identyfikator''', nazywany również '''kluczem''', którym może być zarówno pojedynczy atrybut, jak i również grupa atrybutów. Pozwala on na jednoznaczne odróżnienie danego obiektu od reszty występujących encji. Wśród identyfikatorów wyróżnić można zarówno te naturalne | Pojedynczy byt musi mieć również wyraźnie określony tzw. '''identyfikator''', nazywany również '''kluczem''', którym może być zarówno pojedynczy atrybut, jak i również grupa atrybutów. Pozwala on na jednoznaczne odróżnienie danego obiektu od reszty występujących encji. Wśród identyfikatorów wyróżnić można zarówno te naturalne - numer dowodu, PESEL, numer rejestracyjny, jak i sztuczne - numer pozycji danego produktu w katalogu. Na przykład, na studiach może zdarzyć się, że kilku studentów posiadających takie samo imię i nazwisko - które są atrybutami, jednak jego identyfikatorem jest na przykład numer albumu - każdy student ma swój indywidualnie przypisany numer, który wyróżnia go z całej reszty studentów. | ||
Mianem '''atrybutów deskrypcyjnych''', czy też '''deskryptorów''', określane są takie atrybuty, które nie są identyfikatorami. Wartości te mogą być, w zależności od [[potrzeby informacyjne|potrzeb informacyjnych]], obowiązkowe lub też opcjonalne (D. Olczyk 2010, K. Sacha 2010, s. 85; s. 93; J. Kisielnicki 2013, s. 131; K. Polańska 2015, s. 25). | Mianem '''atrybutów deskrypcyjnych''', czy też '''deskryptorów''', określane są takie atrybuty, które nie są identyfikatorami. Wartości te mogą być, w zależności od [[potrzeby informacyjne|potrzeb informacyjnych]], obowiązkowe lub też opcjonalne (D. Olczyk 2010, K. Sacha 2010, s. 85; s. 93; J. Kisielnicki 2013, s. 131; K. Polańska 2015, s. 25). | ||
| Linia 42: | Linia 33: | ||
Przykładami encji oraz ich atrybutów mogą być: | Przykładami encji oraz ich atrybutów mogą być: | ||
* ''Student'' mający między innymi takie atrybuty jak: Numer albumu, Rok urodzenia, Imię, Nazwisko, czy także Kierunek studiów. | * ''Student'' mający między innymi takie atrybuty jak: Numer albumu, Rok urodzenia, Imię, Nazwisko, czy także Kierunek studiów. | ||
* ''Osoba'', której atrybutami mogą być na przykład Imię, Nazwisko, PESEL, czy też Adres zamieszkania. | * ''Osoba'', której atrybutami mogą być na przykład Imię, Nazwisko, PESEL, czy też Adres zamieszkania. | ||
* ''Pojazd'', który ma swoje atrybuty, w tym między innymi: Marka, Rok produkcji, Model, Numer VIN, czy sam Numer rejestracyjny. | * ''Pojazd'', który ma swoje atrybuty, w tym między innymi: Marka, Rok produkcji, Model, Numer VIN, czy sam Numer rejestracyjny. | ||
Zaprezentowane zostały one również na rysunku 1. | Zaprezentowane zostały one również na rysunku 1. | ||
W przypadku dużych diagramów pomocne może okazać się zastosowanie słownika danych. Przykładowy zapis w takim słowniku może przyjąć na przykład taką formę: | W przypadku dużych diagramów pomocne może okazać się zastosowanie słownika danych. Przykładowy zapis w takim słowniku może przyjąć na przykład taką formę: | ||
:Osoba = *encja* | :Osoba = *encja* PESEL + Imię + Nazwisko + Adres | ||
:Student = *encja* | :Student = *encja* Numer albumu + Imię + Nazwisko + Rok studiów + Adres | ||
Zapisy takie odczytywać można jako: Encja ''Osoba'' złożona jest z takich atrybutów jak: PESEL, Imię, Nazwisko Adres. PESEL jest identyfikatorem encji ''Osoba'' (K. Polańska 2015, s. 25). | Zapisy takie odczytywać można jako: Encja ''Osoba'' złożona jest z takich atrybutów jak: PESEL, Imię, Nazwisko Adres. PESEL jest identyfikatorem encji ''Osoba'' (K. Polańska 2015, s. 25). | ||
===Związek=== | ===Związek=== | ||
[[Plik:Stopnie zwiazkow.png|300px|right|thumb|'''Rys. 2 Stopnie związków''' Źródło: opracowanie własne na podstawie [S. Łecheciński 2012, s. 43 | [[Plik:Stopnie zwiazkow.png|300px|right|thumb|'''Rys. 2 Stopnie związków''' Źródło: opracowanie własne na podstawie [S. Łecheciński 2012, s. 43-44; K. Polańska 2015, s. 27-29] ]] | ||
'''Związek''', czy też '''relacja''' (ang. ''relationship'') jest pewnego rodzaju logicznym powiązaniem lub też sprzężeniem, jakie występuje między poszczególnymi, istniejącymi encjami. Jest to [[informacja]], którą należy przechowywać w danym systemie, ponieważ nie jest możliwe jej wywnioskowanie, pozyskanie, czy także obliczenie z wartości atrybutów danego bytu. Związek pozwala powiązać ze sobą | '''Związek''', czy też '''relacja''' (ang. ''relationship'') jest pewnego rodzaju logicznym powiązaniem lub też sprzężeniem, jakie występuje między poszczególnymi, istniejącymi encjami. Jest to [[informacja]], którą należy przechowywać w danym systemie, ponieważ nie jest możliwe jej wywnioskowanie, pozyskanie, czy także obliczenie z wartości atrybutów danego bytu. Związek pozwala powiązać ze sobą - dwie lub więcej - występujące encje. Każda z relacji musi zostać właściwie nazwana tak, aby modele ER były czytelne i zrozumiałe dla ludzi. Ważnym aspektem związku jest jego liczebność - inaczej nazywana typami związku, a także opcjonalność. Związek w diagramach oznaczany jest najczęściej strzałką, bądź też linią przerywaną lub ciągłą, co jest zależne od cechy jaką jest opcjonalność. Dodatkowo do nich muszą zostać dopisane nazwy, a także określone zakończenia - zależne między innymi od wspomnianej już liczebności danego związku. | ||
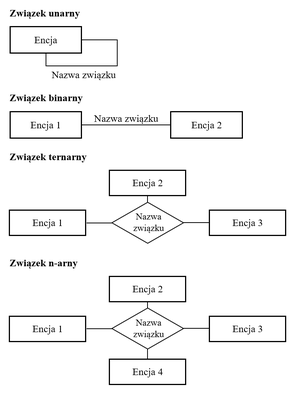
W literaturze, wyróżnić można kilka stopni związków, które zależne są od liczby encji, jakie biorą w nich udział. Są to między innymi relacje: '''dwuargumentowe''', '''jednoargumentowe''', '''trzyargumentowe''', czy także '''wieloargumentowe'''. Najczęściej stosowanymi i rozważanymi są pierwsze związki, nazywane również binarnymi. Budowane są na bazie dwóch różnych obiektów, między którymi pojawia się pewna zależność. Dla odróżnienia, związki jednoargumentowe, nazywane również unarnymi lub rekurencyjnymi, mają wyłącznie jednego uczestnika, czyli także jedną relację. Powstają one w podobnie do związków binarnych, z taką różnicą, że encja jest tylko jedna | W literaturze, wyróżnić można kilka stopni związków, które zależne są od liczby encji, jakie biorą w nich udział. Są to między innymi relacje: '''dwuargumentowe''', '''jednoargumentowe''', '''trzyargumentowe''', czy także '''wieloargumentowe'''. Najczęściej stosowanymi i rozważanymi są pierwsze związki, nazywane również binarnymi. Budowane są na bazie dwóch różnych obiektów, między którymi pojawia się pewna zależność. Dla odróżnienia, związki jednoargumentowe, nazywane również unarnymi lub rekurencyjnymi, mają wyłącznie jednego uczestnika, czyli także jedną relację. Powstają one w podobnie do związków binarnych, z taką różnicą, że encja jest tylko jedna - obiekt jest powiązany sam ze sobą. W takich powiązaniach występować mogą relacje jeden do wielu oraz wiele do wielu. Związki trzyargumentowe, czyli ternarne oraz ostatnie wymienione, nazywane również n-arnymi, prezentują powiązania jakie występują między więcej niż dwoma połączonymi ze sobą encjami. Nie mogą one być bezpośrednio wprowadzane do relacyjnych baz, ponieważ wymagają specjalnych przekształceń. Na rysunku 2 przedstawione zostały przykładowe graficzne prezentacje stopni związków (D. Olczyk 2010, s. 93-94; K. Polańska 2015, s. 25; S. Wrycza i in. 2019, s. 379-382). | ||
==Typy związków== | ==Typy związków== | ||
[[Plik:Typy zwiazkow.png|400px|right|thumb|'''Rys. 3 Typy związków''' Źródło: opracowanie własne na podstawie [D. Olczyk 2010, s. 93 | [[Plik:Typy zwiazkow.png|400px|right|thumb|'''Rys. 3 Typy związków''' Źródło: opracowanie własne na podstawie [D. Olczyk 2010, s. 93-94; C. Orłowski 2012, s. 18; J. Kisielnicki 2013, s. 133; K. Polańska 2015, s. 27-28; S. Wrycza i in. 2019, s. 380] ]] | ||
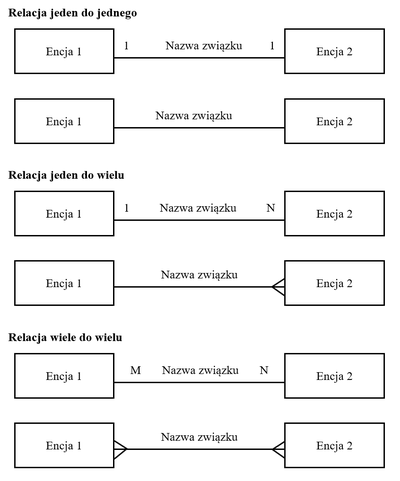
'''Typy''', czy też '''liczebność''' związku pozwala zdefiniować z iloma wystąpieniami | '''Typy''', czy też '''liczebność''' związku pozwala zdefiniować z iloma wystąpieniami danego bytu (encji) można połączyć występowanie innego obiektu. Wyróżnić można wiele typów relacji, jednak do trzech podstawowych, dwuargumentowych związków zalicza się (D. Olczyk 2010, s. 93-94; J. Kisielnicki 2013, s. 135; K. Polańska 2015, s. 25; S. Wrycza i in. 2019, s. 379-380): | ||
* Jeden do jednego (''1 : 1''), | * Jeden do jednego (''1 : 1''), | ||
* Jeden do wielu (''1 : N''), | * Jeden do wielu (''1 : N''), | ||
| Linia 76: | Linia 67: | ||
Związek ten określa, iż jedno wystąpienie danego obiektu (encji) związane jest z większą ilością wystąpień innego bytu, tak samo jak jedno wystąpienie innego bytu może być powiązane z większą ilością wystąpień tego pierwszego obiektu. Budowanie takich związków wydaje się być dla niektórych problematyczne, dlatego też w celu ułatwienia tego procesu wykorzystuje się ich rozbijanie na związki jeden do wielu. Wymagane jest wtedy utworzenie nowego obiektu, który będzie łącznikiem między pozostałymi dwoma, a jego atrybutami będą cechy łączące wcześniejsze encje. Przykładem takiego związku może być zależność jaka występuje pomiędzy ''Studentem'' oraz ''Wykładem''. Student zapisany może być na wiele Wykładów, tak i na dany Wykład zapisanych może być wielu Studentów. | Związek ten określa, iż jedno wystąpienie danego obiektu (encji) związane jest z większą ilością wystąpień innego bytu, tak samo jak jedno wystąpienie innego bytu może być powiązane z większą ilością wystąpień tego pierwszego obiektu. Budowanie takich związków wydaje się być dla niektórych problematyczne, dlatego też w celu ułatwienia tego procesu wykorzystuje się ich rozbijanie na związki jeden do wielu. Wymagane jest wtedy utworzenie nowego obiektu, który będzie łącznikiem między pozostałymi dwoma, a jego atrybutami będą cechy łączące wcześniejsze encje. Przykładem takiego związku może być zależność jaka występuje pomiędzy ''Studentem'' oraz ''Wykładem''. Student zapisany może być na wiele Wykładów, tak i na dany Wykład zapisanych może być wielu Studentów. | ||
Na rysunku 3 przedstawione zostały przykładowe oznaczenia omówionych wyżej liczebności związków, w wybranych notacjach. Pierwszy przykład | Na rysunku 3 przedstawione zostały przykładowe oznaczenia omówionych wyżej liczebności związków, w wybranych notacjach. Pierwszy przykład - poszczególny relacji - jest prezentowany w notacji Chana, drugi - w notacji Martina lub też Crow’s Foot. Jak można zauważyć, w zależności od stosowanej notacji, liczebność jednej ze stron w związku - a dokładniej strony "wielu" - można zaprezentować za pomocą litery np. ''M'' lub ''N'' lub także za pomocą tzw. ''kurzej łapki'', czyli rozgałęzienia linii łączącej encje. | ||
==Opcjonalność relacji== | ==Opcjonalność relacji== | ||
[[Plik:Oznaczenia opcjonalnosci.png|300px|right|thumb|'''Rys. 4 Oznaczenia opcjonalności''' Źródło: Opracowanie własne na podstawie [K. Sacha 2010, s. 86; K. Polańska 2015, s. 30] ]] | [[Plik:Oznaczenia opcjonalnosci.png|300px|right|thumb|'''Rys. 4 Oznaczenia opcjonalności''' Źródło: Opracowanie własne na podstawie [K. Sacha 2010, s. 86; K. Polańska 2015, s. 30] ]] | ||
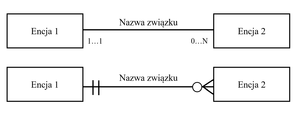
'''Opcjonalność''' rozumiana może być jako minimalna liczebność relacji. Jest to element diagramu, który informuje o tym, czy każda instancja obiektu musi brać udział w konkretnej relacji. Opcjonalność, w zależności od stosowanej notacji, może być przedstawiana w postaci na przykład: kół oraz pionowych kresek lub też symboli: ''0'', ''1'' oraz ''N''. | '''Opcjonalność''' rozumiana może być jako minimalna liczebność relacji. Jest to element diagramu, który informuje o tym, czy każda instancja obiektu musi brać udział w konkretnej relacji. Opcjonalność, w zależności od stosowanej notacji, może być przedstawiana w postaci na przykład: kół oraz pionowych kresek lub też symboli: ''0'', ''1'' oraz ''N''. Oznaczenia w postaci znaków, które umieszcza się nad lub pod linią relacji, stosowane są na przykład w notacji Chana. Natomiast oznaczenia w postaci koła oraz pionowych kresek, które znajdują się na linii, stosowane są między innymi przy notacjach Crow’s Foot, czy Martina, tam gdzie wykorzystuje się tzw. kurze łapki. W takiej sytuacji: koło oznacza brak obowiązku udziału obiektu w relacji, a prostopadła do linii kreska oznacza konieczność jego udziału w danej relacji. Dodatkowo można zaznaczyć, że zastosowanie dwóch pionowych kresek rozumieć można, jako konieczność wystąpienia encji, w danej relacji wyłącznie jeden raz. Rysunek przedstawia przykładowe zastosowanie oznaczenia opcjonalności w dwóch notacjach (K. Sacha 2010, s. 86; K. Polańska 2015, s. 30; S. Wrycza i in. 2019, s. 380). | ||
==Graficzna prezentacja modelu== | ==Graficzna prezentacja modelu== | ||
| Linia 86: | Linia 77: | ||
[[Plik:Elementy ERD w wybranych notacjach.png|400px|left|thumb|'''Rys. 5 Elementy ERD w wybranych notacjach''' Źródło: opracowanie własne na podstawie [D. Olczyk 2010, s. 95] ]] | [[Plik:Elementy ERD w wybranych notacjach.png|400px|left|thumb|'''Rys. 5 Elementy ERD w wybranych notacjach''' Źródło: opracowanie własne na podstawie [D. Olczyk 2010, s. 95] ]] | ||
<br clear=all> | <br clear=all> | ||
{{infobox5|list1={{i5link|a=[[Artefakt]]}} — {{i5link|a=[[Dziedziczenie (informatyka)]]}} — {{i5link|a=[[Baza NoSQL]]}} — {{i5link|a=[[Dane]]}} — {{i5link|a=[[HTML]]}} — {{i5link|a=[[Diagramy przepływu danych]]}} — {{i5link|a=[[Sieć komputerowa]]}} — {{i5link|a=[[SQL]]}} — {{i5link|a=[[Algorytmy szyfrowania]]}} }} | |||
==Bibliografia== | ==Bibliografia== | ||
* Bojarski R. (2012), [https://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-61023513-a6b2-42a9-a5f4-93e3e0138a26 | <noautolinks> | ||
* Chodkowska | * Bojarski R. (2012), ''[https://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-61023513-a6b2-42a9-a5f4-93e3e0138a26 Modele związków encji w bazach danych systemów wspomagających zarządzanie wytwarzaniem]'', Zeszyty Naukowe. Organizacja i Zarządzanie / Politechnika Śląska, Tom 61 | ||
* Chodkowska-Gyurics A. (2014), ''Hurtownie danych. Teoria i praktyka'', Wydawnictwo Naukowe PWN, Warszawa | |||
* Dudek A. (red.) (2011), ''Systemy informatyczne zarządzania Microsoft Business Solutions Navision'', Wydawnictwo Uniwersytetu Ekonomicznego we Wrocławiu, Wrocław | * Dudek A. (red.) (2011), ''Systemy informatyczne zarządzania Microsoft Business Solutions Navision'', Wydawnictwo Uniwersytetu Ekonomicznego we Wrocławiu, Wrocław | ||
* Kisielnicki J. | * Kisielnicki J. (2013), ''Systemy informatyczne zarządzania'', Placet, Warszawa | ||
* Łecheciński S. (2012), | * Łecheciński S. (2012), ''Tworzenie Relacyjnych Modeli Danych'', Studia i Materiały Polskiego Stowarzyszenia Zarządzania Wiedzą, Nr 62 | ||
* Olczyk D. (2010), [ | * Olczyk D. (2010), ''[https://zeszyty-naukowe.wwsi.edu.pl/zeszyty/zeszyt4/Modelowanie_Strukturalne_-_Definicje_Notacja_Techniki_I_Narzedzia.pdf Modelowanie strukturalne: definicje, notacje, techniki i narzędzia]'', Zeszyty Naukowe Warszawskiej Wyższej Szkoły Informatyki, Nr 4 | ||
* Orłowski C., Lipski J., Loska A. (2012), ''Informatyka i komputerowe wspomaganie prac inżynierskich'', Polskie Wydawnictwo Ekonomiczne, Warszawa | * Orłowski C., Lipski J., Loska A. (2012), ''Informatyka i komputerowe wspomaganie prac inżynierskich'', Polskie Wydawnictwo Ekonomiczne, Warszawa | ||
* Polańska K. (red.) (2015), ''Wstęp do informatyki gospodarczej. Zajęcia laboratoryjne'', Szkoła Główna Handlowa w Warszawie, Warszawa | * Polańska K. (red.) (2015), ''Wstęp do informatyki gospodarczej. Zajęcia laboratoryjne'', Szkoła Główna Handlowa w Warszawie, Warszawa | ||
* Sacha K. (red.) ( | * Sacha K. (red.) (2012), ''Inżynieria oprogramowania'', Wydawnictwo Naukowe PWN, Warszawa | ||
* Szczęśniak B. (2013), [ | * Szczęśniak B. (2013), ''[https://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-e94ce5d9-fab7-45c1-a9c8-b75025ff5635 Koncepcja zastosowania arkusza kalkulacyjnego do wspomagania tworzenia dokumentów w procesie produkcji taśm blachy]'', Systemy Wspomagania w Inżynierii Produkcji, Tom 2(4) | ||
* | * Szczęśniak B., Bujanowska A. (2011), ''Koncepcja zastosowania arkusza kalkulacyjnego do wspomagania procesu przeglądów urządzeń w wybranym szpitalu'', Studia i Materiały Polskiego Stowarzyszenia Zarządzania Wiedzą, Nr 45 | ||
* Wrycza S., Maślankowski J. (red.) (2019), ''Informatyka ekonomiczna. Teoria i zastosowania'', Wydawnictwo Naukowe PWN, Warszawa | * Wrycza S., Maślankowski J. (red.) (2019), ''Informatyka ekonomiczna. Teoria i zastosowania'', Wydawnictwo Naukowe PWN, Warszawa | ||
</noautolinks> | |||
{{a|Żaneta Golonka}} | {{a|Żaneta Golonka}} | ||
[[Kategoria: | [[Kategoria:Systemy informacyjne]] | ||
{{#metamaster:description|Model związków encji to metoda projektowania danych. Diagramy ER pokazują encje, relacje i atrybuty przechowywane w systemie informacyjnym.}} | |||
Aktualna wersja na dzień 00:31, 10 sty 2024
Model związków encji, określany jest również jako: model ER lub ERD. Skróty te pochodzą od angielskiej nazwy Entity Relationship Diagram. Metoda zaprezentowana została po raz pierwszy przez Petera Chena w 1976 roku. Późniejszych, drobnych modyfikacji w diagramie dokonali między innymi Charles Bachman oraz James Martin. Jest to jedna z najpopularniejszych, dotychczas zaprojektowanych, metod modelowania danych.
Diagramy te pokazują pewnego rodzaju obiekty, nazywane również encjami, których cechy charakterystyczne, czyli atrybuty, a także relacje jakie między nimi zachodzą, przechowywane są w systemie informacyjnym. Warto zauważyć, że dla danego systemu tworzony jest jeden, spójny diagram. Nie przeprowadza się dekompozycji modelu na mniejsze części. Można dokonać jego podziału jedynie w sytuacji, kiedy dąży się do zaprezentowania i wydruku systemu.
Należy zauważyć, że wyróżnić można różne notacje diagramów. Obecnie wśród najpopularniejszych wymienia się między innymi notację: Chena, Bachmana, Crow’s Foot, Martina, czy też Barkera. W zależności od stosowanej notacji, odmienne mogą być na przykład oznaczenia poszczególnych związków, ich liczebności, czy też opcjonalności, jakie występują w ERD (D. Olczyk 2010, s. 93; K. Sacha 2010, s. 86; K. Polańska 2015, s. 24-25; S. Wrycza i in. 2019, s. 379).
TL;DR
Model związków encji (ER lub ERD) to metoda modelowania danych, która opisuje obiekty (encje), ich cechy (atrybuty) oraz relacje między nimi. Encje są przedstawiane jako prostokąty, a atrybuty jako owale. Związki są reprezentowane przez strzałki lub linie przerywane. Istnieją różne notacje ER, które różnią się oznaczeniami związków i atrybutów. W zależności od notacji, związki mogą mieć różne typy (jeden do jednego, jeden do wielu, wiele do wielu) i opcjonalność. Model ER jest używany do projektowania baz danych i systemów informacyjnych.
Elementy modelu
W skład modelu związków encji wchodzą elementy takie jak: encja, atrybut, związek.
Encja
Encja (ang. entity) wyraża różnego rodzaju obiekty, składniki rzeczywistości, czy też szeroko pojęty byt. W diagramie prezentowana jest najczęściej w formie prostokąta o ostrych, bądź zaokrąglonych rogach. Nazwa danej encji umiejscowiona jest zazwyczaj w pierwszym wersie, a dodatkowo oznaczana jest innym kolorem, bądź też rodzajem czcionki - tak, aby łatwo było ją dostrzec. Nazwą jest rzeczownik, który w przypadku jednej encji jest w liczbie pojedynczej, natomiast w przypadku magazynu danych jest w liczbie mnogiej. Przykładami pojedynczych obiektów mogą być: przedmiot, pojazd, osoba, książka, zamówienie, jak i również pojęcie. Natomiast magazynami danych nazwać można na przykład osoby, zdarzenia, faktury, zamówienia, itd..
Dwie podstawowe własności encji:
- obiekty wzajemnie się wkluczają, co oznacza, że dana encja może reprezentować jeden, konkretny składnik rzeczywistości,
- wszystkie obiekty muszą być wyraźnie identyfikowane, co oznacza, że dana instancja musi się jednoznacznie wyróżniać od pozostałych instancji tego typu.
Z tego też powodu, warto rozróżnić pojęcie encji / typu encji od wystąpienia / instancji encji. Konkretne obiekty, jakie pojawiają się w świecie, są określane mianem instancji. Przykładowo: encją będzie Uniwersytet, zaś jej instancją będzie jeden konkretny na przykład Uniwersytet Ekonomiczny w Krakowie (D. Olczyk 2010, s. 93; K. Sacha 2010, s. 85; J. Kisielnicki 2013, s. 130; K. Polańska 2015, s. 25; S. Wrycza i in. 2019, s. 379).
Atrybut
Atrybut (ang. attribute) to pewnego rodzaju cechy charakterystyczne dla danej encji, które są przechowywane w danym systemie. Jej zadaniem jest opisywanie, czy też określanie danego bytu. Każdy poszczególny obiekt musi zostać opisany przez minimum jeden atrybut, choć często jest to pewien ich zbiór. W diagramie prezentowane mogą być między innymi jako owal.
Pojedynczy byt musi mieć również wyraźnie określony tzw. identyfikator, nazywany również kluczem, którym może być zarówno pojedynczy atrybut, jak i również grupa atrybutów. Pozwala on na jednoznaczne odróżnienie danego obiektu od reszty występujących encji. Wśród identyfikatorów wyróżnić można zarówno te naturalne - numer dowodu, PESEL, numer rejestracyjny, jak i sztuczne - numer pozycji danego produktu w katalogu. Na przykład, na studiach może zdarzyć się, że kilku studentów posiadających takie samo imię i nazwisko - które są atrybutami, jednak jego identyfikatorem jest na przykład numer albumu - każdy student ma swój indywidualnie przypisany numer, który wyróżnia go z całej reszty studentów.
Mianem atrybutów deskrypcyjnych, czy też deskryptorów, określane są takie atrybuty, które nie są identyfikatorami. Wartości te mogą być, w zależności od potrzeb informacyjnych, obowiązkowe lub też opcjonalne (D. Olczyk 2010, K. Sacha 2010, s. 85; s. 93; J. Kisielnicki 2013, s. 131; K. Polańska 2015, s. 25).
Przykładami encji oraz ich atrybutów mogą być:
- Student mający między innymi takie atrybuty jak: Numer albumu, Rok urodzenia, Imię, Nazwisko, czy także Kierunek studiów.
- Osoba, której atrybutami mogą być na przykład Imię, Nazwisko, PESEL, czy też Adres zamieszkania.
- Pojazd, który ma swoje atrybuty, w tym między innymi: Marka, Rok produkcji, Model, Numer VIN, czy sam Numer rejestracyjny.
Zaprezentowane zostały one również na rysunku 1.
W przypadku dużych diagramów pomocne może okazać się zastosowanie słownika danych. Przykładowy zapis w takim słowniku może przyjąć na przykład taką formę:
- Osoba = *encja* PESEL + Imię + Nazwisko + Adres
- Student = *encja* Numer albumu + Imię + Nazwisko + Rok studiów + Adres
Zapisy takie odczytywać można jako: Encja Osoba złożona jest z takich atrybutów jak: PESEL, Imię, Nazwisko Adres. PESEL jest identyfikatorem encji Osoba (K. Polańska 2015, s. 25).
Związek
Związek, czy też relacja (ang. relationship) jest pewnego rodzaju logicznym powiązaniem lub też sprzężeniem, jakie występuje między poszczególnymi, istniejącymi encjami. Jest to informacja, którą należy przechowywać w danym systemie, ponieważ nie jest możliwe jej wywnioskowanie, pozyskanie, czy także obliczenie z wartości atrybutów danego bytu. Związek pozwala powiązać ze sobą - dwie lub więcej - występujące encje. Każda z relacji musi zostać właściwie nazwana tak, aby modele ER były czytelne i zrozumiałe dla ludzi. Ważnym aspektem związku jest jego liczebność - inaczej nazywana typami związku, a także opcjonalność. Związek w diagramach oznaczany jest najczęściej strzałką, bądź też linią przerywaną lub ciągłą, co jest zależne od cechy jaką jest opcjonalność. Dodatkowo do nich muszą zostać dopisane nazwy, a także określone zakończenia - zależne między innymi od wspomnianej już liczebności danego związku.
W literaturze, wyróżnić można kilka stopni związków, które zależne są od liczby encji, jakie biorą w nich udział. Są to między innymi relacje: dwuargumentowe, jednoargumentowe, trzyargumentowe, czy także wieloargumentowe. Najczęściej stosowanymi i rozważanymi są pierwsze związki, nazywane również binarnymi. Budowane są na bazie dwóch różnych obiektów, między którymi pojawia się pewna zależność. Dla odróżnienia, związki jednoargumentowe, nazywane również unarnymi lub rekurencyjnymi, mają wyłącznie jednego uczestnika, czyli także jedną relację. Powstają one w podobnie do związków binarnych, z taką różnicą, że encja jest tylko jedna - obiekt jest powiązany sam ze sobą. W takich powiązaniach występować mogą relacje jeden do wielu oraz wiele do wielu. Związki trzyargumentowe, czyli ternarne oraz ostatnie wymienione, nazywane również n-arnymi, prezentują powiązania jakie występują między więcej niż dwoma połączonymi ze sobą encjami. Nie mogą one być bezpośrednio wprowadzane do relacyjnych baz, ponieważ wymagają specjalnych przekształceń. Na rysunku 2 przedstawione zostały przykładowe graficzne prezentacje stopni związków (D. Olczyk 2010, s. 93-94; K. Polańska 2015, s. 25; S. Wrycza i in. 2019, s. 379-382).
Typy związków
Typy, czy też liczebność związku pozwala zdefiniować z iloma wystąpieniami danego bytu (encji) można połączyć występowanie innego obiektu. Wyróżnić można wiele typów relacji, jednak do trzech podstawowych, dwuargumentowych związków zalicza się (D. Olczyk 2010, s. 93-94; J. Kisielnicki 2013, s. 135; K. Polańska 2015, s. 25; S. Wrycza i in. 2019, s. 379-380):
- Jeden do jednego (1 : 1),
- Jeden do wielu (1 : N),
- Wiele do wielu (M : N).
Jeden do jednego
Związek ten określa, iż każde wystąpienie danego obiektu (encji) związane jest wyłącznie z pojedynczym wystąpieniem innego bytu. Jest to jedna z najprostszych relacji, jaką można wyróżnić między encjami. Reguła ta działa w dwie strony, jednak zawsze musi zostać spełniona. W praktyce ta forma związków występuje stosunkowo rzadko, dlatego też w momencie pojawienia się takiej relacji należy upewnić się, czy właściwie określono między innymi: atrybuty encji, czy też liczebność związku. Przykładem związku jeden do jednego może być relacja jaka zachodzi między Pracownikiem, a przydzielonym mu Miejscem parkingowym, czy także Kierownikiem a Działem. I tak na przykład: Pracownik w organizacji ma przypisane konkretne Miejsce, a to Miejsce jest przypisane do konkretnego Pracownika. Kierownik zarządza jednym Działem, a Dział zarządzany jest przez jednego Kierownika.
Jeden do wielu
Związek ten określa, iż jedno wystąpienie danego obiektu (encji) związane jest z większą ilością wystąpień innego bytu. Natomiast jedno wystąpienie innego bytu połączone jest wyłącznie z jednym wystąpieniem tego pierwszego obiektu. W praktyce, jest to najczęściej występujący rodzaj relacji jaka zachodzi między encjami. Jako przykłady związku jeden do wielu można podać relacje, jakie zachodzą na przykład między: Klientem za Zamówieniem, czy też Firmą a Działem. I tak na przykład: Klient składa wiele Zamówień. Konkretne Zamówienie jest składane przez danego Klienta. W Firmie istnieje wiele Działów. Konkretny Dział istnieje w danej Firmie.
Wiele do wielu
Związek ten określa, iż jedno wystąpienie danego obiektu (encji) związane jest z większą ilością wystąpień innego bytu, tak samo jak jedno wystąpienie innego bytu może być powiązane z większą ilością wystąpień tego pierwszego obiektu. Budowanie takich związków wydaje się być dla niektórych problematyczne, dlatego też w celu ułatwienia tego procesu wykorzystuje się ich rozbijanie na związki jeden do wielu. Wymagane jest wtedy utworzenie nowego obiektu, który będzie łącznikiem między pozostałymi dwoma, a jego atrybutami będą cechy łączące wcześniejsze encje. Przykładem takiego związku może być zależność jaka występuje pomiędzy Studentem oraz Wykładem. Student zapisany może być na wiele Wykładów, tak i na dany Wykład zapisanych może być wielu Studentów.
Na rysunku 3 przedstawione zostały przykładowe oznaczenia omówionych wyżej liczebności związków, w wybranych notacjach. Pierwszy przykład - poszczególny relacji - jest prezentowany w notacji Chana, drugi - w notacji Martina lub też Crow’s Foot. Jak można zauważyć, w zależności od stosowanej notacji, liczebność jednej ze stron w związku - a dokładniej strony "wielu" - można zaprezentować za pomocą litery np. M lub N lub także za pomocą tzw. kurzej łapki, czyli rozgałęzienia linii łączącej encje.
Opcjonalność relacji
Opcjonalność rozumiana może być jako minimalna liczebność relacji. Jest to element diagramu, który informuje o tym, czy każda instancja obiektu musi brać udział w konkretnej relacji. Opcjonalność, w zależności od stosowanej notacji, może być przedstawiana w postaci na przykład: kół oraz pionowych kresek lub też symboli: 0, 1 oraz N. Oznaczenia w postaci znaków, które umieszcza się nad lub pod linią relacji, stosowane są na przykład w notacji Chana. Natomiast oznaczenia w postaci koła oraz pionowych kresek, które znajdują się na linii, stosowane są między innymi przy notacjach Crow’s Foot, czy Martina, tam gdzie wykorzystuje się tzw. kurze łapki. W takiej sytuacji: koło oznacza brak obowiązku udziału obiektu w relacji, a prostopadła do linii kreska oznacza konieczność jego udziału w danej relacji. Dodatkowo można zaznaczyć, że zastosowanie dwóch pionowych kresek rozumieć można, jako konieczność wystąpienia encji, w danej relacji wyłącznie jeden raz. Rysunek przedstawia przykładowe zastosowanie oznaczenia opcjonalności w dwóch notacjach (K. Sacha 2010, s. 86; K. Polańska 2015, s. 30; S. Wrycza i in. 2019, s. 380).
Graficzna prezentacja modelu
Elementy graficzne poszczególnych diagramów różnić mogą się od siebie w zależności od przyjętej notacji. Na rysunku znajdują się graficzne prezentacje najważniejszych elementów z wybranych notacji.
| Model związków encji — artykuły polecane |
| Artefakt — Dziedziczenie (informatyka) — Baza NoSQL — Dane — HTML — Diagramy przepływu danych — Sieć komputerowa — SQL — Algorytmy szyfrowania |
Bibliografia
- Bojarski R. (2012), Modele związków encji w bazach danych systemów wspomagających zarządzanie wytwarzaniem, Zeszyty Naukowe. Organizacja i Zarządzanie / Politechnika Śląska, Tom 61
- Chodkowska-Gyurics A. (2014), Hurtownie danych. Teoria i praktyka, Wydawnictwo Naukowe PWN, Warszawa
- Dudek A. (red.) (2011), Systemy informatyczne zarządzania Microsoft Business Solutions Navision, Wydawnictwo Uniwersytetu Ekonomicznego we Wrocławiu, Wrocław
- Kisielnicki J. (2013), Systemy informatyczne zarządzania, Placet, Warszawa
- Łecheciński S. (2012), Tworzenie Relacyjnych Modeli Danych, Studia i Materiały Polskiego Stowarzyszenia Zarządzania Wiedzą, Nr 62
- Olczyk D. (2010), Modelowanie strukturalne: definicje, notacje, techniki i narzędzia, Zeszyty Naukowe Warszawskiej Wyższej Szkoły Informatyki, Nr 4
- Orłowski C., Lipski J., Loska A. (2012), Informatyka i komputerowe wspomaganie prac inżynierskich, Polskie Wydawnictwo Ekonomiczne, Warszawa
- Polańska K. (red.) (2015), Wstęp do informatyki gospodarczej. Zajęcia laboratoryjne, Szkoła Główna Handlowa w Warszawie, Warszawa
- Sacha K. (red.) (2012), Inżynieria oprogramowania, Wydawnictwo Naukowe PWN, Warszawa
- Szczęśniak B. (2013), Koncepcja zastosowania arkusza kalkulacyjnego do wspomagania tworzenia dokumentów w procesie produkcji taśm blachy, Systemy Wspomagania w Inżynierii Produkcji, Tom 2(4)
- Szczęśniak B., Bujanowska A. (2011), Koncepcja zastosowania arkusza kalkulacyjnego do wspomagania procesu przeglądów urządzeń w wybranym szpitalu, Studia i Materiały Polskiego Stowarzyszenia Zarządzania Wiedzą, Nr 45
- Wrycza S., Maślankowski J. (red.) (2019), Informatyka ekonomiczna. Teoria i zastosowania, Wydawnictwo Naukowe PWN, Warszawa
Autor: Żaneta Golonka