Model Baumola: Różnice pomiędzy wersjami
(LinkTitles.) |
m (cleanup bibliografii i rotten links) |
||
| (Nie pokazano 12 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
'''[[Model]] Baumola''' zwany też modelem '''Baumola-Allaisa-Tobina (BAT)''' jest to model zarządzania środkami pieniężnymi.W roku 1952 Wiliam Baumol przedstawił pomysł na [[zarządzanie]] nadwyżką środków finansowych poprzez optymalne wykorzystanie wielkości dostaw zapasów. Doszedł do wniosku, że pieniądze można również traktować jako specyficzny rodzaj zapasów, taki który jest niezbędny przy prowadzeniu działalności. Kiedy mówimy o optymalizacji środków pieniężnych i ich salda, można zauważyć wyraźną analogię między gotówką i materiałami. Kiedy porównamy ze sobą zarządzanie gotówką i [[zarządzanie zapasami]] wynika z tego, że nadwyżki ze środków pieniężnych trzymane są w przedsiębiorstwach jako papietry wartościowe, najczęściej są to [[bony skarbowe]] [Uziębo A., 2016, s. 524]. Model Baumola opiera się na modelu ekonomicznej wielkości dostaw czyli tzw. Modelu EOQ (economic order qantity). Do głównych założeń modelu BAT można zaliczyć: | '''[[Model]] Baumola''' zwany też modelem '''Baumola-Allaisa-Tobina (BAT)''' jest to model zarządzania środkami pieniężnymi.W roku 1952 Wiliam Baumol przedstawił pomysł na [[zarządzanie]] nadwyżką środków finansowych poprzez optymalne wykorzystanie wielkości dostaw zapasów. Doszedł do wniosku, że pieniądze można również traktować jako specyficzny rodzaj zapasów, taki który jest niezbędny przy prowadzeniu działalności. Kiedy mówimy o optymalizacji środków pieniężnych i ich salda, można zauważyć wyraźną analogię między gotówką i materiałami. Kiedy porównamy ze sobą zarządzanie gotówką i [[zarządzanie zapasami]] wynika z tego, że nadwyżki ze środków pieniężnych trzymane są w przedsiębiorstwach jako papietry wartościowe, najczęściej są to [[bony skarbowe]] [Uziębo A., 2016, s. 524]. Model Baumola opiera się na modelu ekonomicznej wielkości dostaw czyli tzw. Modelu EOQ (economic order qantity). Do głównych założeń modelu BAT można zaliczyć: | ||
* możliwe do zaprognozowania oraz stałe w całym okresie (roku) [[zapotrzebowanie]] na gotówkę, | * możliwe do zaprognozowania oraz stałe w całym okresie (roku) [[zapotrzebowanie]] na gotówkę, | ||
* stały i przewidywalny dopływ gotówki, | * stały i przewidywalny dopływ gotówki, | ||
* stałą w całym okresie stopę procentową przy inwestycji w[[ papiery wartościowe]], | * stałą w całym okresie stopę procentową przy inwestycji w[[ papiery wartościowe]], | ||
* rytmiczne wpływy gotówki, | * rytmiczne wpływy gotówki, | ||
* natychmiastowe transfery gotówki, [Machała 2014, s. 423] | * natychmiastowe transfery gotówki, [Machała 2014, s. 423] | ||
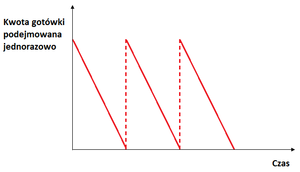
Patrząc na powyższe założenia można wyciągnąć wnioski iż środki pieniężne są zużywane w sposób jednostajny. W momencie kiedy osiągają poziom minimalny czyli ten równy 0, wtedy to równoważności środków pieniężnych zamieniane są na gotówkę w takiej wysokości aby osiągnąć maksymalny poziom. Wtedy następuje powtórzenie cyklu. Zależność tą pokazuje wykres przedstawiony na rysunku 1.[Pluta W. 2013., s. 93] | Patrząc na powyższe założenia można wyciągnąć wnioski iż środki pieniężne są zużywane w sposób jednostajny. W momencie kiedy osiągają poziom minimalny czyli ten równy 0, wtedy to równoważności środków pieniężnych zamieniane są na gotówkę w takiej wysokości aby osiągnąć maksymalny poziom. Wtedy następuje powtórzenie cyklu. Zależność tą pokazuje wykres przedstawiony na rysunku 1.[Pluta W. 2013., s. 93] | ||
[[Plik:Modelbaumolawykres.png|300px|right|thumb|Rys. 1 Zmiany stanu gotówki wg modelu BAT [Szymański P.,2007 s. 158-160] ]] | [[Plik:Modelbaumolawykres.png|300px|right|thumb|Rys. 1 Zmiany stanu gotówki wg modelu BAT [Szymański P.,2007 s. 158-160] ]] | ||
Zadaniem modelu Baumola jest ukazanie dolnego marginesu bezpieczeństwa a w momencie kiedy stan środków bieżących przybliża się do tego punktu wtedy nastepuje [[sprzedaż]] bonów skarbowych lub innych papierów wartościowych po to aby uzupełnić środki[Pluta W. 2013., s. 93]. W modelu Baumola optymalny poziom środków pieniężnych obliczamy w następujący sposób: | Zadaniem modelu Baumola jest ukazanie dolnego marginesu bezpieczeństwa a w momencie kiedy stan środków bieżących przybliża się do tego punktu wtedy nastepuje [[sprzedaż]] bonów skarbowych lub innych papierów wartościowych po to aby uzupełnić środki[Pluta W. 2013., s. 93]. W modelu Baumola optymalny poziom środków pieniężnych obliczamy w następujący sposób: | ||
'''C''' = <math>\sqrt{\dfrac{2*T*F}{R}}</math> | '''C''' = <math>\sqrt{\dfrac{2*T*F}{R}}</math> | ||
| Linia 34: | Linia 15: | ||
Gdzie: | Gdzie: | ||
'''C'''-optymalny poziom gotówki | '''C'''-optymalny poziom gotówki | ||
'''T'''-zapotrzebowanie na środki pieniężne w całym okresie badanym (rok) | '''T'''-zapotrzebowanie na środki pieniężne w całym okresie badanym (rok) | ||
'''F'''-stałe [[koszty]] transferu gotówki | '''F'''-stałe [[koszty]] transferu gotówki | ||
'''R'''-[[koszt]] alternatywny utrzymania gotówki | '''R'''-[[koszt]] alternatywny utrzymania gotówki | ||
Wzór ten pochodzi mianowicie z tego, że jeżeli poziom środków pieniężnych ma być optymalny to musi zachodzić następująca równość: | Wzór ten pochodzi mianowicie z tego, że jeżeli poziom środków pieniężnych ma być optymalny to musi zachodzić następująca równość: | ||
'''K<sub>A</sub> = K<sub>T</sub>''', czyli [[koszt alternatywny]] musi równać się kosztom transakcyjnym. Te z kolei wielkości wylicza się następująco: | '''K<sub>A</sub> = K<sub>T</sub>''', czyli [[koszt alternatywny]] musi równać się kosztom transakcyjnym. Te z kolei wielkości wylicza się następująco: | ||
K<sub>A</sub>= <math>\dfrac{C*R}{2}</math | K<sub>A</sub>= <math>\dfrac{C*R}{2}</math> | ||
K<sub>T</sub>= <math>\dfrac{T*F}{C}</math | K<sub>T</sub>= <math>\dfrac{T*F}{C}</math> | ||
[Szymański P., 2007, s. 158] | [Szymański P., 2007, s. 158] | ||
Model Baumola służy do wyznaczania właściwego poziomu gotówki, który będzie minimalizował całkowity koszt transakcji i kosztów alternatywnych w wyniku utrzymywania danego poziomu środków pieniężnych [Pluta W. 2013., s. 93]. | Model Baumola służy do wyznaczania właściwego poziomu gotówki, który będzie minimalizował całkowity koszt transakcji i kosztów alternatywnych w wyniku utrzymywania danego poziomu środków pieniężnych [Pluta W. 2013., s. 93]. | ||
<google>n</google> | |||
==TL;DR== | |||
Model Baumola, zwany także modelem Baumola-Allaisa-Tobina, jest modelem zarządzania środkami pieniężnymi. Opiera się na optymalnym wykorzystaniu wielkości dostaw zapasów, traktując pieniądze jako specyficzny rodzaj zapasów. Model ten ma za zadanie określić optymalny poziom gotówki, minimalizujący koszty transakcji i koszty alternatywne. Jednak model ten ma wiele ograniczeń i trudności w praktycznym zastosowaniu, przez co nie jest często używany w firmach. | |||
==Ograniczenia w modelu Baumola== | ==Ograniczenia w modelu Baumola== | ||
| Linia 51: | Linia 37: | ||
W przypadku planowania optymalnego poziomu środków finansowych Model Baumola jest pomocnym narzędziem, jednak posiada on wiele ograniczeń które obniżają jego [[przydatność]]. Model bazuje na założeniach które dla przedsiębiorstwa są [[zbyt]] mało realistyczne z tego powodu nie wykorzystuje się go w pracy [Uziębo A.,2016, s. 524]. | W przypadku planowania optymalnego poziomu środków finansowych Model Baumola jest pomocnym narzędziem, jednak posiada on wiele ograniczeń które obniżają jego [[przydatność]]. Model bazuje na założeniach które dla przedsiębiorstwa są [[zbyt]] mało realistyczne z tego powodu nie wykorzystuje się go w pracy [Uziębo A.,2016, s. 524]. | ||
{{infobox5|list1={{i5link|a=[[Analiza wykorzystania majątku]]}} — {{i5link|a=[[Stopa dyskontowa]]}} — {{i5link|a=[[Próg rentowności]]}} — {{i5link|a=[[RAROC]]}} — {{i5link|a=[[Metoda annuitetowa]]}} — {{i5link|a=[[Wskaźnik rotacji]]}} — {{i5link|a=[[Model Blacka Scholesa]]}} — {{i5link|a=[[Kredyt obrotowy]]}} — {{i5link|a=[[Teoria cyklu koniunkturalnego M. Kaleckiego]]}} — {{i5link|a=[[Konsolidacja przedsiębiorstw]]}} }} | |||
==Bibliografia== | ==Bibliografia== | ||
* Machała R. | <noautolinks> | ||
* Pluta W. Krótkoterminowe zarządzanie kapitałem- Jak zachować płynność finansową | * Machała R. (2014), ''Zarządzanie Finansami i Wycena Firmy'', Oficyna Wydawnicza UNIMEX, Wrocław | ||
* Szymański P. [ | * Pluta W. (2013), ''Krótkoterminowe zarządzanie kapitałem - Jak zachować płynność finansową'', PWE, Warszawa | ||
* | * Szymański P. (2007), ''[https://pbc.biaman.pl/Content/1211/szymanski-zarzadzanie_majatkiem_obrotowym.pdf Zarządzanie majątkiem obrotowym w procesie kreowania wartości przedsiębiorstwa]'', Wydawnictwo Petros, Łódź | ||
* Uziębło A. (2016), ''Optymalizacja gospodarowania środkami pieniężnymi w przedsiębiorstwie ciepłowniczym z wykorzystaniem modelu Millera-Orra'', Szczecin | |||
</noautolinks> | |||
[[Kategoria:Zarządzanie finansami]] | [[Kategoria:Zarządzanie finansami]] | ||
{{a|Joanna Witowska}} | {{a|Joanna Witowska}} | ||
{{#metamaster:description|Model Baumola to efektywny sposób zarządzania środkami pieniężnymi. Minimalizuje koszty transakcji i utrzymania gotówki, uwzględniając zapotrzebowanie, dopływ środków i stopę procentową.}} | |||
Aktualna wersja na dzień 20:20, 1 gru 2023
Model Baumola zwany też modelem Baumola-Allaisa-Tobina (BAT) jest to model zarządzania środkami pieniężnymi.W roku 1952 Wiliam Baumol przedstawił pomysł na zarządzanie nadwyżką środków finansowych poprzez optymalne wykorzystanie wielkości dostaw zapasów. Doszedł do wniosku, że pieniądze można również traktować jako specyficzny rodzaj zapasów, taki który jest niezbędny przy prowadzeniu działalności. Kiedy mówimy o optymalizacji środków pieniężnych i ich salda, można zauważyć wyraźną analogię między gotówką i materiałami. Kiedy porównamy ze sobą zarządzanie gotówką i zarządzanie zapasami wynika z tego, że nadwyżki ze środków pieniężnych trzymane są w przedsiębiorstwach jako papietry wartościowe, najczęściej są to bony skarbowe [Uziębo A., 2016, s. 524]. Model Baumola opiera się na modelu ekonomicznej wielkości dostaw czyli tzw. Modelu EOQ (economic order qantity). Do głównych założeń modelu BAT można zaliczyć:
- możliwe do zaprognozowania oraz stałe w całym okresie (roku) zapotrzebowanie na gotówkę,
- stały i przewidywalny dopływ gotówki,
- stałą w całym okresie stopę procentową przy inwestycji wpapiery wartościowe,
- rytmiczne wpływy gotówki,
- natychmiastowe transfery gotówki, [Machała 2014, s. 423]
Patrząc na powyższe założenia można wyciągnąć wnioski iż środki pieniężne są zużywane w sposób jednostajny. W momencie kiedy osiągają poziom minimalny czyli ten równy 0, wtedy to równoważności środków pieniężnych zamieniane są na gotówkę w takiej wysokości aby osiągnąć maksymalny poziom. Wtedy następuje powtórzenie cyklu. Zależność tą pokazuje wykres przedstawiony na rysunku 1.[Pluta W. 2013., s. 93]
Zadaniem modelu Baumola jest ukazanie dolnego marginesu bezpieczeństwa a w momencie kiedy stan środków bieżących przybliża się do tego punktu wtedy nastepuje sprzedaż bonów skarbowych lub innych papierów wartościowych po to aby uzupełnić środki[Pluta W. 2013., s. 93]. W modelu Baumola optymalny poziom środków pieniężnych obliczamy w następujący sposób:
C =
Gdzie: C-optymalny poziom gotówki T-zapotrzebowanie na środki pieniężne w całym okresie badanym (rok) F-stałe koszty transferu gotówki R-koszt alternatywny utrzymania gotówki
Wzór ten pochodzi mianowicie z tego, że jeżeli poziom środków pieniężnych ma być optymalny to musi zachodzić następująca równość: KA = KT, czyli koszt alternatywny musi równać się kosztom transakcyjnym. Te z kolei wielkości wylicza się następująco: KA=
KT= [Szymański P., 2007, s. 158]
Model Baumola służy do wyznaczania właściwego poziomu gotówki, który będzie minimalizował całkowity koszt transakcji i kosztów alternatywnych w wyniku utrzymywania danego poziomu środków pieniężnych [Pluta W. 2013., s. 93].
TL;DR
Model Baumola, zwany także modelem Baumola-Allaisa-Tobina, jest modelem zarządzania środkami pieniężnymi. Opiera się na optymalnym wykorzystaniu wielkości dostaw zapasów, traktując pieniądze jako specyficzny rodzaj zapasów. Model ten ma za zadanie określić optymalny poziom gotówki, minimalizujący koszty transakcji i koszty alternatywne. Jednak model ten ma wiele ograniczeń i trudności w praktycznym zastosowaniu, przez co nie jest często używany w firmach.
Ograniczenia w modelu Baumola
Mimo, iż model Baumola to klasyczny model zarządzania środkami pieniężnymi to ciężko jest stosować go w codziennym życiu. Głównym ograniczeniem jest to, że firma musi równomiernie zużywać zapasy by model się sprawdzał. W praktyce jest to prawie niewykonalne. Również utrudnieniem jest to że w przedsiębiorstwie ciężko jest określić precyzyjny popyt na środki finansowe, także wydatki które ponosi firma nie rozkładają się jednakowo przez cały okres. Kolejnym ograniczeniem w stosowaniu modelu jest również zmienna w czasie prowizja od transakcji, która często może być negocjowana i zależy od wielkości transakcji i od terminu wykupu.Następnym utrudnieniem jest to, że oprocentowanie rachunku bieżącego jest zmienne w czasie, podobnie jak rentowność bonów skarbowych, która dodatkowo uzależniona jest od terminu wykupu odrębnych serii [Szymański P.,2007 s. 158-160].
W przypadku planowania optymalnego poziomu środków finansowych Model Baumola jest pomocnym narzędziem, jednak posiada on wiele ograniczeń które obniżają jego przydatność. Model bazuje na założeniach które dla przedsiębiorstwa są zbyt mało realistyczne z tego powodu nie wykorzystuje się go w pracy [Uziębo A.,2016, s. 524].
| Model Baumola — artykuły polecane |
| Analiza wykorzystania majątku — Stopa dyskontowa — Próg rentowności — RAROC — Metoda annuitetowa — Wskaźnik rotacji — Model Blacka Scholesa — Kredyt obrotowy — Teoria cyklu koniunkturalnego M. Kaleckiego — Konsolidacja przedsiębiorstw |
Bibliografia
- Machała R. (2014), Zarządzanie Finansami i Wycena Firmy, Oficyna Wydawnicza UNIMEX, Wrocław
- Pluta W. (2013), Krótkoterminowe zarządzanie kapitałem - Jak zachować płynność finansową, PWE, Warszawa
- Szymański P. (2007), Zarządzanie majątkiem obrotowym w procesie kreowania wartości przedsiębiorstwa, Wydawnictwo Petros, Łódź
- Uziębło A. (2016), Optymalizacja gospodarowania środkami pieniężnymi w przedsiębiorstwie ciepłowniczym z wykorzystaniem modelu Millera-Orra, Szczecin
Autor: Joanna Witowska