Rozkład Poissona: Różnice pomiędzy wersjami
m (Czyszczenie tekstu) |
m (cleanup bibliografii i rotten links) |
||
| (Nie pokazano 6 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
'''Rozkład Poissona''' jest jednym z rozkładów zmiennych losowych skokowych (A. Zeliaś 1996, s. 39) Ma on charakterystyczną [[własność]] wiążącą go z rozkładem dwumianowym, gdyż otrzymujemy go biorąc pod uwagę ciąg serii doświadczeń zrealizowanych według schematu Bernoulliego (J. F. C. Kingman 2002, s. 65) Jest to rozkład asymetryczny. Nazwę wziął od nazwiska osoby, która go wprowadziła. Był to Simeon-Denis Poisson i opisał ten rozkład w swoim dziele: "Procedes des Ragles Generales du Calcul des Probabilites. Bachelier, Imprimeur-Libraire pour les Mathematiques", wydanym w Paryżu w 1837. | '''Rozkład Poissona''' jest jednym z rozkładów zmiennych losowych skokowych (A. Zeliaś 1996, s. 39) Ma on charakterystyczną [[własność]] wiążącą go z rozkładem dwumianowym, gdyż otrzymujemy go biorąc pod uwagę ciąg serii doświadczeń zrealizowanych według schematu Bernoulliego (J. F. C. Kingman 2002, s. 65) Jest to rozkład asymetryczny. Nazwę wziął od nazwiska osoby, która go wprowadziła. Był to Simeon-Denis Poisson i opisał ten rozkład w swoim dziele: "Procedes des Ragles Generales du Calcul des Probabilites. Bachelier, Imprimeur-Libraire pour les Mathematiques", wydanym w Paryżu w 1837. | ||
| Linia 31: | Linia 16: | ||
Załóżmy teraz, że w rozkładzie dwumianowym prawdopodobieństwo p jest zależne od n w taki sposób, że podczas zmierzania n do nieskończoności, p zmierza do zera. Mówiąc bardziej szczegółowo, należy założyć, że [[wartość oczekiwana]] zmiennej losowej X liczby realizacji zdarzeń "A" w każdej serii doświadczeń <math>E (X) = np. = {\lambda} > 0</math>. | Załóżmy teraz, że w rozkładzie dwumianowym prawdopodobieństwo p jest zależne od n w taki sposób, że podczas zmierzania n do nieskończoności, p zmierza do zera. Mówiąc bardziej szczegółowo, należy założyć, że [[wartość oczekiwana]] zmiennej losowej X liczby realizacji zdarzeń "A" w każdej serii doświadczeń <math>E (X) = np. = {\lambda} > 0</math>. | ||
<google>n</google> | |||
Oznacza to wielkość stałą, zatem <math>p = \frac {\lambda}{n}</math>. Otrzymujemy w ten sposób przy: n → ∞, p → 0 i np. = λ funkcję prawdopodobieństwa rozkładu Poissona o postaci: | Oznacza to wielkość stałą, zatem <math>p = \frac {\lambda}{n}</math>. Otrzymujemy w ten sposób przy: n → ∞, p → 0 i np. = λ funkcję prawdopodobieństwa rozkładu Poissona o postaci: | ||
| Linia 39: | Linia 26: | ||
* k = 0,1,2,...,n | * k = 0,1,2,...,n | ||
* λ = np. - wartość oczekiwana. | * λ = np. - wartość oczekiwana. | ||
Powyższy wzór otrzymujemy z relacji <math>P_n (X = k)=\binom{n}{k}p^kq^{n-k}</math> zamiast prawdopodobieństwa p podstawiając <math>\frac {\lambda}{n}</math> mamy równanie: | Powyższy wzór otrzymujemy z relacji <math>P_n (X = k)=\binom{n}{k}p^kq^{n-k}</math> zamiast prawdopodobieństwa p podstawiając <math>\frac {\lambda}{n}</math> mamy równanie: | ||
| Linia 146: | Linia 132: | ||
Strumień Poissona nie jest tylko wykorzystywany do modelowania rozkładu czasu zgłoszeń przychodzących, ale jest on także wykorzystywany do wyznaczania czasów | Strumień Poissona nie jest tylko wykorzystywany do modelowania rozkładu czasu zgłoszeń przychodzących, ale jest on także wykorzystywany do wyznaczania czasów | ||
obsługi tych zgłoszeń. W wielu modelach klas ruchu występuje zatem "poissonowski" strumień obsługi. | obsługi tych zgłoszeń. W wielu modelach klas ruchu występuje zatem "poissonowski" strumień obsługi. | ||
{{infobox5|list1={{i5link|a=[[Zmienna losowa]]}} — {{i5link|a=[[Prawdopodobieństwo warunkowe]]}} — {{i5link|a=[[Rozkład normalny]]}} — {{i5link|a=[[Estymator obciążony]]}} — {{i5link|a=[[Mediana wzór]]}} — {{i5link|a=[[Średnia]]}} — {{i5link|a=[[Przedział ufności]]}} — {{i5link|a=[[Estymator nieobciążony]]}} — {{i5link|a=[[Estymacja]]}} }} | |||
==Bibliografia== | ==Bibliografia== | ||
<noautolinks> | <noautolinks> | ||
* Dodge Y. | * Dodge Y. (2008), ''The Concise Encyclopedia of Statistics'', Springer, New York | ||
* Greene W. | * Greene W. (2003), ''Econometric Analysis'', Prentice Hall | ||
* Kingman J. | * Kingman J. (2002), ''Procesy Poissona'', Wydawnictwo Naukowe PWN, Warszawa | ||
* Steczkowski J., Woźniak M., Zając K., Zeliaś A. | * Steczkowski J., Woźniak M., Zając K., Zeliaś A. (1996), ''Statystyka matematyczna w zastosowaniach'', Wydawnictwo Akademii Ekonomicznej w Krakowie, Kraków | ||
* Woźniak M. | * Woźniak M. (2002), ''Statystyka ogólna'', Wydawnictwo Akademii Ekonomicznej w Krakowie, Kraków | ||
</noautolinks> | </noautolinks> | ||
{{a|Paweł Fiedor, Sylwia Gęborys, Kinga Węgrzyn}} | {{a|Paweł Fiedor, Sylwia Gęborys, Kinga Węgrzyn}} | ||
[[Kategoria: | [[Kategoria:Rozkład]] | ||
{{#metamaster:description|Rozkład Poissona to asymetryczny rozkład zmiennych losowych skokowych. Jest przybliżeniem rozkładu dwumianowego, używanym dla dużej próby i małego prawdopodobieństwa sukcesu.}} | {{#metamaster:description|Rozkład Poissona to asymetryczny rozkład zmiennych losowych skokowych. Jest przybliżeniem rozkładu dwumianowego, używanym dla dużej próby i małego prawdopodobieństwa sukcesu.}} | ||
Aktualna wersja na dzień 15:04, 12 sty 2024
Rozkład Poissona jest jednym z rozkładów zmiennych losowych skokowych (A. Zeliaś 1996, s. 39) Ma on charakterystyczną własność wiążącą go z rozkładem dwumianowym, gdyż otrzymujemy go biorąc pod uwagę ciąg serii doświadczeń zrealizowanych według schematu Bernoulliego (J. F. C. Kingman 2002, s. 65) Jest to rozkład asymetryczny. Nazwę wziął od nazwiska osoby, która go wprowadziła. Był to Simeon-Denis Poisson i opisał ten rozkład w swoim dziele: "Procedes des Ragles Generales du Calcul des Probabilites. Bachelier, Imprimeur-Libraire pour les Mathematiques", wydanym w Paryżu w 1837.
Rozkład Poissona jest przybliżeniem rozkładu dwumianowego dla dużej próby oraz małego prawdopodobieństwa sukcesu.
Należy założyć, w tym przypadku, że liczba doświadczeń n nieograniczenie wzrośnie a równolegle zmaleje prawdopodobieństwo p realizacji zdarzenia "A" w każdej serii doświadczeń. Prawdopodobieństwo wystąpienia zdarzenia jest bardzo małe, bliskie zera, dlatego nazywamy go często prawem rzadkich zdarzeń lub też prawem małych liczb.
Biorąc pod uwagę zmienną losową X o rozkładzie dwumianowym, a więc mającą wartość k = 0,1,…, n z prawdopodobieństwami:
Przy czym:
- 0 < p < 1
- - rozkład dwumianowy określa wystąpienie k razy zdarzenia "A", w n niezależnych doświadczeniach,
- p - prawdopodobieństwo,
- q - prawdopodobieństwo zdarzenia przeciwnego.
Załóżmy teraz, że w rozkładzie dwumianowym prawdopodobieństwo p jest zależne od n w taki sposób, że podczas zmierzania n do nieskończoności, p zmierza do zera. Mówiąc bardziej szczegółowo, należy założyć, że wartość oczekiwana zmiennej losowej X liczby realizacji zdarzeń "A" w każdej serii doświadczeń .
Oznacza to wielkość stałą, zatem . Otrzymujemy w ten sposób przy: n → ∞, p → 0 i np. = λ funkcję prawdopodobieństwa rozkładu Poissona o postaci:
Przy czym:
- k = 0,1,2,...,n
- λ = np. - wartość oczekiwana.
Powyższy wzór otrzymujemy z relacji zamiast prawdopodobieństwa p podstawiając mamy równanie:
Używając uproszczeń możemy otrzymać:
W liczniku ułamka drugiego obserwujemy k czynników, gdyż w jego mianowniku występuje , należy jedynie podzielić przez n każdy z czynników licznika. Drugi ułamek przyjmie wówczas postać:
Każdy z powyższych czynników dąży do 1, gdy n → ∞, co stanowi o dążeniu do jedności całego iloczynu ze skończoną liczbą czynników. Dla n → ∞ mianownik ułamka trzeciego w poprzednim wzorze dąży do 1, ponieważ wykładnik potęgi jest skończony. Aby więc uznać za prawdziwy dany wzór, wystarczy udowodnić, że licznik trzeciego ułamka dąży do . Podstawiając , oraz uzyskujemy:
- n → ∞,
- z → ∞.
Dzieje się tak ponieważ:
- z → ∞.
Iloczyn dąży więc do .
Mówimy, że rozkład Poissona jest rozkładem jednoparametrycznym, gdyż funkcja prawdopodobieństwa zależy od wartości λ. (M. Woźniak 2002, s. 119)
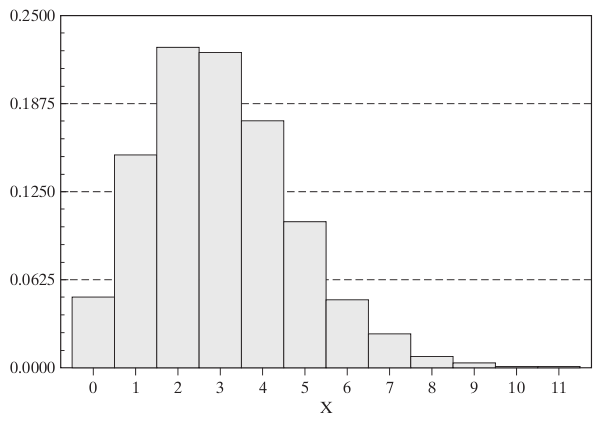
Histogram dla rozkładu Poissona o parametrze równym 3 wygląda następująco:
TL;DR
Rozkład Poissona jest jednym z rozkładów zmiennych losowych skokowych i ma charakterystyczne własności. Jest przybliżeniem rozkładu dwumianowego dla dużej próby i małego prawdopodobieństwa sukcesu. Rozkład ten znajduje zastosowanie w wielu dziedzinach, takich jak statystyka, fizyka, demografia czy ekonometria. Jest również wykorzystywany do modelowania czasu zgłoszeń i obsługi.
Parametry
Rozkład Poissona zależy od jednego parametru λ, będącego zawsze dodatnim. Wartość oczekiwana jest równa E (x) = λ = np, zaś odchylenie standardowe σ(X) = √λ = √np [A. Zeliaś 1996, s. 41-42]
Najważniejsze parametry przyjmują dla rozkładu Poissona następujące wartości:
Mediana: wynosi około
Moda: największa liczba całkowita mniejsza lub równa λ
Wariancja: λ
Skośność:
Własności
Dla λ dążącego do nieskończoności rozkład Poissona może być przybliżony rozkładem normalnym o średniej λ i wariancji λ.
Jeśli zmienne losowe mają rozkład Poissona z parametrem i są niezależne, to suma N takich zmiennych oznaczona jako Y będzie miała rozkład Poissona o parametrze będącym sumą parametrów zmiennych wchodzących w jej skład, co zapisujemy następująco:
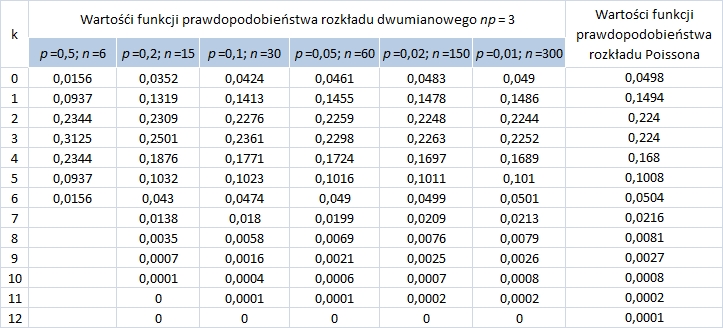
Są stablicowane wartości funkcji prawdopodobieństwa dla różnych λ i różnych n i k. Jeśli więc znamy n i p, możemy korzystając z tablic znaleźć . Powyższe twierdzenie ukazuje, że dla przybliżonego oszacowania prawdopodobieństw w rozkładzie dwumianowym istnieje możliwość posłużenia się rozkładem Poissona. Ma to istotne znaczenie, gdy n jest duże (n ≥ 25, p ≤ 0,02). Poniższa tabela ilustruje zbieżność rozkładu dwumianowego do rozkładu Poissona [A. Zeliaś 1996, s. 39-41]
Zastosowanie
Według K. Zająca rozkład Poissona ma zastosowanie w:
- statystycznym odbiorze towarów,
- statystycznej kontroli jakości produkcji,
- fizyce eksperymentalnej,
- opisywaniu uszkodzeń różnego rodzaju urządzeń,
- demografii,
- opisaniu procesów transportowych [A. Zeliaś 1996, s. 43].
Rozkład Poissona znajduje zastosowanie m.in. w określaniu następujących zdarzeń (Y. Dodge 2008, s. 426):
- liczba cząstek emitowanych przez substancję radioaktywną,
- liczba rozmów zarejestrowanych przez centralę,
- liczba wypadków przytrafiających się ubezpieczonej osobie,
- liczba bakterii w preparacie mikroskopowym,
Rozkład ten znajduje także szerokie zastosowanie w ekonometrii, m.in. w modelowaniu patentów, zbrodni czy popytu na usługi medyczne (W. Greene 2002, s. 856)
Strumień Poissona
Ze względu na prostotę jego matematycznego opisu nazywany jest również strumieniem najprostszym. W przypadku strumienia Poissona rozkład czasu pomiędzy kolejnymi zgłoszeniami, jest rozkładem wykładniczym z parametrem λ.
Jego gęstość wyraża się wzorem:
ƒ(t)=(λe)^(-λt)
Natomiast dystrybuanta tego rozkładu wyrażona jest zależnością:
F (t)=(1-e)^(-λt)
Strumień Poissona należy do rodziny strumieni rekurencyjnych - strumieni Palma. Są to strumienie pojedyncze i stacjonarne, dla których czasy pomiędzy kolejnymi zgłoszeniami są zmiennymi losowymi o takim samym rozkładzie f (t). Strumień najprostszy jest zatem szczególnym przypadkiem rozkładu Palma.
Interesującą własnością strumienia Poissona jest możliwość otrzymania różnych strumieni rekurencyjnych poprzez wykonywanie pewnych operacji na strumieniach zgłoszeń: superpozycję, przesiewanie czy też przesiewanie przypadkowe.
Przykładowo dokonując superpozycji dwóch strumieni Poissona o intensywnościach: λ1 i λ2, w rezultacie otrzymamy również strumień Poissona, którego intensywność strumienia wypadkowego λ3 wynosi:
λ3 = λ1 + λ2.
Strumień Poissona nie jest tylko wykorzystywany do modelowania rozkładu czasu zgłoszeń przychodzących, ale jest on także wykorzystywany do wyznaczania czasów obsługi tych zgłoszeń. W wielu modelach klas ruchu występuje zatem "poissonowski" strumień obsługi.
| Rozkład Poissona — artykuły polecane |
| Zmienna losowa — Prawdopodobieństwo warunkowe — Rozkład normalny — Estymator obciążony — Mediana wzór — Średnia — Przedział ufności — Estymator nieobciążony — Estymacja |
Bibliografia
- Dodge Y. (2008), The Concise Encyclopedia of Statistics, Springer, New York
- Greene W. (2003), Econometric Analysis, Prentice Hall
- Kingman J. (2002), Procesy Poissona, Wydawnictwo Naukowe PWN, Warszawa
- Steczkowski J., Woźniak M., Zając K., Zeliaś A. (1996), Statystyka matematyczna w zastosowaniach, Wydawnictwo Akademii Ekonomicznej w Krakowie, Kraków
- Woźniak M. (2002), Statystyka ogólna, Wydawnictwo Akademii Ekonomicznej w Krakowie, Kraków
Autor: Paweł Fiedor, Sylwia Gęborys, Kinga Węgrzyn