Kurtoza

Kurtoza
Polecane artykuły
Metody statystyczne Percentyl Średnia Rozstęp Rozkład normalny Wariancja Współczynnik korelacji rang Spearmana Test zgodności chi-kwadrat Dominanta

Kurtoza jest to względna miara koncentracji i spłaszczenia rozkładu (termin stosowany w statystyce i rachunku prawdopodobieństwa). Określa rozmieszczenie i koncentrację wartości (zbiorowości) w pobliżu średniej. Występuje on w postaci stosującej moment centralny czwartego rzędu: $K={\frac {m_{4}}{s^{4}}}$

Gdzie:

• $m_{4}$ oznacza moment centralny rzędu czwartego
• $s^{2}$ jest odchyleniem standardowym podniesionym do czwartej potęgi.

Dla szeregu szczegółowego, prostego:

$M_{4}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{4}$

Kurtoza z próby dla szeregu rozdzielczego punktowego:

$M_{4}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{4}f_{i}$

Gdzie:

• $x_{i}$ to i-ta wartość cechy,
• ${\overline {x}}$ to średnia z próby,
• $n$ to liczebność z próby.

Kurtoza z próby dla szeregu przedziałowego do wzoru powyższego należy wprowadzić środki przedziałów losowych.

Miara spłaszczenia rozkładu częstości, czyli kurtoza może być obliczana jako wartość absolutna lub wartość względna. Kurtoza absolutna jest zawsze liczbą nieujemną, natomiast kurtoza względna może przyjmować zarówno wartości ujemne, jak i dodatnie. Wartości dodatnie charakteryzują rozkłady bardziej spiczaste w porównaniu do rozkładu normalnego, czyli są tzw. leptokurtyczne. Wartości ujemne charakteryzują rozkłady bardziej spłaszczone niż rozkłady normalne i są nazywane platokurtycznymi. (A. D. Aczel, 2018, s. 51-52)

Im wyższa kurtoza tym większe skupienie zbiorowości wokół wartości średniej, co daje wyraz w większej smukłości krzywej rozkładu. Mała jej wartość daje efekt odwrotny czyli większy rozrzut wartości, słabą koncentrację i, co za tym idzie, spłaszczenie krzywej liczebności.

Dla rozkładu normalnego przyjmuje się wartość kurtozy równą 3, dla wartości większych od 3 rozkład jest bardziej wysmukły a dla wartości mniejszych bardziej spłaszczony.

Często stosuje się inną formułę obliczania kurtozy ze względu na podane powyżej zależności od wartości 3. W ramach udogodnienia sprowadzono wzór do postaci, dla której kurtoza rozkładu normalnego przyjmuje wartość 0, nosi on nazwę współczynnika ekscesu

$K={\frac {m_{4}}{s^{4}}}-3$

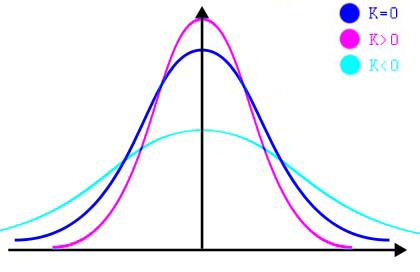
Tutaj interpretacja jest podobna:

• dla K=0 rozkład ma kształt normalny (rozkład mezokurtyczny),
• dla K>0 rozkład jest bardziej wysmukły niż normalny (rozkład leptokurtyczny), większe skupienie wartości wokół średniej,
• dla K<0 rozkład jest mniej wysmukły niż normalny (rozkład platykurtyczny), większe spłaszczenie rozkładu.

Wraz ze wzrostem liczebności prób różnice między wartościami ocen estymatorów obciążonych i nieobciążonych stają się nieistotne i zmierzają do zera. Można zatem wysnuć wniosek, że przy dużych próbach nie ma znaczenia czy korzystamy ze wzoru na estymator obciążony czy nieobciążony. (D. Witkowska, 2016, s. 35)

Z obliczania kurtozy często korzystają inwestorzy, ponieważ daje ona informacje o ryzyku i stopie zwrotu z inwestycji. Wysoka kurtoza stopy zwrotu zwiększa prawdopodobieństwo osiągnięcia wyższej wartości stopy zwrotu z inwestycji. Zatem inwestorzy są skłonni zapłacić więcej za inwestycje o rozkładzie leptokurtycznym, niż za inwestycje o rozkładzie platykurtycznym. Poznanie rzeczywistego rozkładu stopy zwrotu danej inwestycji pozwala na lepsze zarządzanie ryzykiem oraz portfelem inwestora, a także pozwala skonstruować w jakim przedziale inwestor może oczekiwać stopy zwrotu. (W. Dębski, 2014, s. 616-618)

Estymator nieobciążony kurtozy jest określony następującym wzorem:
$K={\frac {n(n+1)}{(n-1)(n-2)(n-3)}}\sum _{i=1}^{N}({\frac {x_{i}-{\overline {x}}}{s}})^{4}-{\frac {3(n-1)^{2}}{(n-2)(n-3)}}$

Bibliografia

• Aczel A. D. (2018) Statystyka w zarządzaniu, Wydawnictwo Naukowe PWN
• Budny K. (2015) Wybrane własności kurtozy wektora losowego, Zeszyty Naukowe Uniwersytetu Ekonomicznego w Krakowie
• Dębski W. (2014) Rynek finansowy i jego mechanizmy. Podstawy teorii i praktyki, Wydawnictwo Naukowe PWN
• Górka J. (2007) Kurtoza w procesach generowanych przez model RCA GARCH
• Sobczyk M. (1995) Statystyka, Wydawnictwo PWN, Warszawa
• Warsza Z. L., Korczyński M. J. (2014) Statystyki skośności i kurtozy małych próbek pomiarowych z populacji o rozkładzie normalnym i kilku innych, Wydawnictwo PAK
• Witkowska D. (2016) Zmiana warunków funkcjonowania a efektywność inwestycyjna otwartych funduszy emerytalnych, Wydawnictwo Uniwersytetu Łódzkiego
• Woźniak M. (red.) (1997) Statystyka opisowa, Wydawnictwo AE, Kraków
• Zając K. (1994) Zarys metod statystycznych, Wydawnictwo PWE, Warszawa
• Zelias A. (2000) Metody statystyczne, Wydawnictwo PWE, Warszawa

Autor: Sebastian Głuszek, Magdalena Rzepiszczak