Punkt nasycenia: Różnice pomiędzy wersjami
m (Infobox update) |
(LinkTitles.) |
||
| Linia 17: | Linia 17: | ||
'''Punkt nasycenia''' - optymalna wysokość opodatkowania, która pozwala przynosić maksymalne korzyści dla budżetu (zyski).Punkt nasycenia wywodzi się z Krzywej Laffera przedstawiającej związek pomiędzy wysokością stopy podatkowej a wielkością wpływów z podatków. Określa on poziom podatków powyżej którego zwiększenie stóp podatkowych prowadzi do zmniejszenia dochodów budżetowych. | '''Punkt nasycenia''' - optymalna wysokość opodatkowania, która pozwala przynosić maksymalne korzyści dla budżetu (zyski).Punkt nasycenia wywodzi się z Krzywej Laffera przedstawiającej związek pomiędzy wysokością stopy podatkowej a wielkością wpływów z podatków. Określa on poziom podatków powyżej którego zwiększenie stóp podatkowych prowadzi do zmniejszenia dochodów budżetowych. | ||
Idea punktu nasycenia jest efektem badań ekonomii [[podaż]]owej wskazującej jak podatki i inne bodźce wpływają na wielkość produkcji w gospodarce, odpowiadającą pełnemu wykorzystaniu zdolności wytwórczych. | Idea punktu nasycenia jest efektem badań ekonomii [[podaż]]owej wskazującej jak podatki i inne bodźce wpływają na wielkość produkcji w gospodarce, odpowiadającą pełnemu wykorzystaniu [[zdolności]] wytwórczych. | ||
==Odpowiedni poziom podatków== | ==Odpowiedni poziom podatków== | ||
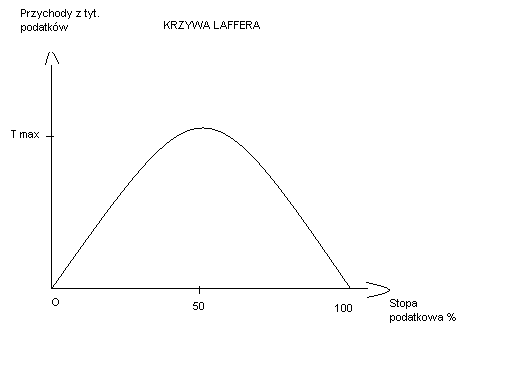
Zgodnie z [[Krzywa Laffera|Krzywą Laffera]] przy stopie opodatkowania równej zeru [[dochody]] państwa wyniosłyby również zero. Jednak gdyby stopa opodatkowania wynosiła 100% dochody państwa pozostałyby na zerowym poziomie. Wynika to z tego, iż nie istniałaby żadna [[motywacja do pracy]], gdyż wszystkie zarobki obywatele oddawaliby państwu w formie podatku. Stąd też zgodnie z teorią Laffera dochody budżetu będą rosły na początku wraz ze wzrostem stopy podatkowej, lecz po przekroczeniu pewnego poziomu wynoszącego t* dalsze zwiekszenie opodatkowania likwiduje motywacje do pracy co powoduje zmniejszenie się podatków. | Zgodnie z [[Krzywa Laffera|Krzywą Laffera]] przy stopie opodatkowania równej zeru [[dochody]] państwa wyniosłyby również zero. Jednak gdyby stopa opodatkowania wynosiła 100% dochody państwa pozostałyby na zerowym poziomie. Wynika to z tego, iż nie istniałaby żadna [[motywacja do pracy]], gdyż wszystkie [[zarobki]] obywatele oddawaliby państwu w formie podatku. Stąd też zgodnie z teorią Laffera dochody budżetu będą rosły na początku wraz ze wzrostem stopy podatkowej, lecz po przekroczeniu pewnego poziomu wynoszącego t* dalsze zwiekszenie opodatkowania likwiduje motywacje do pracy co powoduje zmniejszenie się podatków. | ||
[[Grafika:Krzywa Laffera.png]] | [[Grafika:Krzywa Laffera.png]] | ||
Wersja z 06:53, 21 maj 2020
| Punkt nasycenia |
|---|
| Polecane artykuły |
Punkt nasycenia - optymalna wysokość opodatkowania, która pozwala przynosić maksymalne korzyści dla budżetu (zyski).Punkt nasycenia wywodzi się z Krzywej Laffera przedstawiającej związek pomiędzy wysokością stopy podatkowej a wielkością wpływów z podatków. Określa on poziom podatków powyżej którego zwiększenie stóp podatkowych prowadzi do zmniejszenia dochodów budżetowych.
Idea punktu nasycenia jest efektem badań ekonomii podażowej wskazującej jak podatki i inne bodźce wpływają na wielkość produkcji w gospodarce, odpowiadającą pełnemu wykorzystaniu zdolności wytwórczych.
Odpowiedni poziom podatków
Zgodnie z Krzywą Laffera przy stopie opodatkowania równej zeru dochody państwa wyniosłyby również zero. Jednak gdyby stopa opodatkowania wynosiła 100% dochody państwa pozostałyby na zerowym poziomie. Wynika to z tego, iż nie istniałaby żadna motywacja do pracy, gdyż wszystkie zarobki obywatele oddawaliby państwu w formie podatku. Stąd też zgodnie z teorią Laffera dochody budżetu będą rosły na początku wraz ze wzrostem stopy podatkowej, lecz po przekroczeniu pewnego poziomu wynoszącego t* dalsze zwiekszenie opodatkowania likwiduje motywacje do pracy co powoduje zmniejszenie się podatków.
Bibliografia
- Begg.D Mikroekonomia Polskie Wydawnictwo Ekonomiczne, Warszawa 2007
- Sloman J. Podstawy ekonomiiPolskie Wydawnictwo Ekonomiczne, Warszawa 2001
Autor: Magdalena Mazurek