Wykres pudełkowy: Różnice pomiędzy wersjami
m (cleanup bibliografii i rotten links) |
m (cleanup bibliografii i rotten links) |
||
| (Nie pokazano 12 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
'''Wykres pudełkowy''' nazywany często wykresem skrzynkowym, ramkowym lub wykresem "ramka - wąsy" (z języka angielskiego - ''box plot''). Jest jednym z narzędzi [[Metody statystyczne|statystycznych metod]] [[Zarządzanie jakością|zarządzania jakością]]. Wykresy pudełkowe opracowywane są w oparciu o wartości [[Statystyka opisowa|statystyk opisowych]], dlatego ich zastosowanie ogranicza się do cech liczbowych. Stanowią prostą formę graficznej prezentacji '''rozkładu cechy statystycznej'''. Pozwalają na ujęcie na jednym rysunku wszystkich wiadomości, które dotyczą położenia, kształtu a także rozkładu empirycznego badanej cechy. Charakteryzuje je duża przejrzystość i zwięzłość. (M. Trzęsiok 2014, s.107) | |||
Wykres został zaproponowany przez '''Johna Tukeya''' w książce "Explanatory Data Analysis", wydanej w 1997 roku. Tukey uważa, że wymyślony przez niego wykres ma duża [[wartość]] i pozwala na odkrycie czegoś, czego się nie spodziewaliśmy- "The gratest value of a picture is when it forces us to notice what we never expected to see". | |||
==TL;DR== | ==TL;DR== | ||
Wykres pudełkowy, znany też jako wykres skrzynkowy, ramkowy lub ramka-wąsy, jest narzędziem statystycznym do prezentacji rozkładu cechy statystycznej. Składa się z prostokąta, osi współrzędnych i wąsów. Wykres ma formę minimalistyczną, ale przekazuje wiele informacji. Istnieją różne typy wykresów pudełkowych, najpopularniejszy to wykres z medianą, kwartylami i wartościami minimalną i maksymalną. Wykres pudełkowy jest używany do analizy rozproszenia i kształtu danych. Ma wiele zastosowań, m.in. w analizie danych statystycznych i porównywaniu rozkładów zmiennych. | Wykres pudełkowy, znany też jako wykres skrzynkowy, ramkowy lub ramka-wąsy, jest narzędziem statystycznym do prezentacji rozkładu cechy statystycznej. Składa się z prostokąta, osi współrzędnych i wąsów. Wykres ma formę minimalistyczną, ale przekazuje wiele informacji. Istnieją różne typy wykresów pudełkowych, najpopularniejszy to wykres z medianą, kwartylami i wartościami minimalną i maksymalną. Wykres pudełkowy jest używany do analizy rozproszenia i kształtu danych. Ma wiele zastosowań, m.in. w analizie danych statystycznych i porównywaniu rozkładów zmiennych. | ||
==Opis wykresu== | ==Opis wykresu== | ||
Wykres składa się z '''prostokąta''' (pudełka), '''osi współrzędnych''' i tak zwanych '''wąsów''', czyli odległości wartości minimalnej i maksymalnej od pudełka. Wykres ma formę minimalistyczną, ponieważ przedstawia '''tylko 5 informacji''' i chociaż wydaję się, że jest to niewiele, wykres ramka-wąsy przekazuje nam na bardzo dużo wiadomości. Najczęściej do jego sporządzenia musimy znać dokładne wartości: pierwszego i trzeciego kwartyla, mediany oraz minimum i maksimum. Dzięki tym danym możemy badać poziom rozproszenia danej czy odległości mediany od minimum i maksimum | Wykres składa się z '''prostokąta''' (pudełka), '''osi współrzędnych''' i tak zwanych '''wąsów''', czyli odległości wartości minimalnej i maksymalnej od pudełka. Wykres ma formę minimalistyczną, ponieważ przedstawia '''tylko 5 informacji''' i chociaż wydaję się, że jest to niewiele, wykres ramka-wąsy przekazuje nam na bardzo dużo wiadomości. Najczęściej do jego sporządzenia musimy znać dokładne wartości: pierwszego i trzeciego kwartyla, mediany oraz minimum i maksimum. Dzięki tym danym możemy badać poziom rozproszenia danej czy odległości mediany od minimum i maksimum (J. Łuczak 2007, s.255-258) | ||
Długość prostokąta reprezentuje '''[[rozstęp]] ćwiartkowy IQR''', obejmujący 50% środkowych obserwacji. Pudełko jest rozdzielone pionową linią, która wyznacza '''wartość mediany'''. Dzieli ona przedział ćwiartkowy na dwa obszary, w których znajduje się '''25% obserwacji'''. Wąsy łączą pudełko z największą i najmniejszą wartością badanej zmiennej odpowiednio z przedziału (Q1-1,5*IQR; Q1) oraz (Q3; Q3+1,5 IQR). W pierwszym przedziale znajduje się 25% obserwacji o wartościach niższych od dolnego kwartyla a w drugim przedziale 25% obserwacji o wartościach wyższych od górnego kwartyla (A. Malarska 2005, s.26-27)) | |||
Długość prostokąta reprezentuje '''[[rozstęp]] ćwiartkowy IQR''', obejmujący 50% środkowych obserwacji. Pudełko jest rozdzielone pionową linią, która wyznacza '''wartość mediany'''. Dzieli ona przedział ćwiartkowy na dwa obszary, w których znajduje się '''25% obserwacji'''. Wąsy łączą pudełko z największą i najmniejszą wartością badanej zmiennej odpowiednio z przedziału (Q1-1,5*IQR; Q1) oraz (Q3; Q3+1,5 IQR). W pierwszym przedziale znajduje się 25% obserwacji o wartościach niższych od dolnego kwartyla a w drugim przedziale 25% obserwacji o wartościach wyższych od górnego kwartyla | |||
<google>n</google> | |||
==Typy wykresów pudełkowych== | ==Typy wykresów pudełkowych== | ||
Wyróżnia się następujące typy '''wykresów pudełkowych''': | Wyróżnia się następujące typy '''wykresów pudełkowych''': | ||
1. [[Średnia]]/błąd standardowy/odchylenie standardowe | |||
2. [[Mediana]]/[[kwartyl]]e/minimum, maksimum | 1. [[Średnia]]/błąd standardowy/odchylenie standardowe | ||
3. Średnia/odchylenie standardowe/minimum maksimum | |||
4. Średnia/przedział ufności/odchylenie standardowe | 2. [[Mediana]]/[[kwartyl]]e/minimum, maksimum | ||
Należy zaznaczyć, że najczęściej spotykanym typem jest nr 2. | |||
3. Średnia/odchylenie standardowe/minimum maksimum | |||
4. Średnia/przedział ufności/odchylenie standardowe | |||
Należy zaznaczyć, że najczęściej spotykanym typem jest nr 2. | |||
==Sporządzanie i charakterystyka wykresu pudełkowego== | ==Sporządzanie i charakterystyka wykresu pudełkowego== | ||
Aby sporządzić wykres należy: | Aby sporządzić wykres należy: | ||
* Narysować oś liczbową, na której odmierza się wartości badanej cechy. | * Narysować oś liczbową, na której odmierza się wartości badanej cechy. | ||
* Umieścić wzdłuż osi pudełko (skrzynkę), którego lewy bok wyznacza wartość kwartyla 1, natomiast prawy bok- wartość kwartyla 3. | * Umieścić wzdłuż osi pudełko (skrzynkę), którego lewy bok wyznacza wartość kwartyla 1, natomiast prawy bok - wartość kwartyla 3. | ||
* Uzupełnić wykres dwoma odcinkami, które znajdują się na zewnątrz pudełka (tzw.: wąsy). | * Uzupełnić wykres dwoma odcinkami, które znajdują się na zewnątrz pudełka (tzw.: wąsy). | ||
Wykres pudełkowy posiada dwa [[warianty]]: | Wykres pudełkowy posiada dwa [[warianty]]: | ||
*'''prosty'''- bazuje na głównych statystykach; | * '''prosty''' - bazuje na głównych statystykach; | ||
*'''złożony'''- używany do prezentacji wartości odstających, tzw. '''outlierów'''; | * '''złożony''' - używany do prezentacji wartości odstających, tzw. '''outlierów'''; | ||
'''[[Wariant]] prosty''' | |||
Do stworzenia prostego wykresu pudełkowego niezbędne jest 5 wartości: | '''[[Wariant]] prosty''' | ||
*Max- wartość maksymalna | |||
*Q3- kwartyl 3 | Do stworzenia prostego wykresu pudełkowego niezbędne jest 5 wartości: | ||
*Me- mediana | * Max - wartość maksymalna | ||
*Q1- kwartyl 1 | * Q3 - kwartyl 3 | ||
*Min- wartość minimalna | * Me - mediana | ||
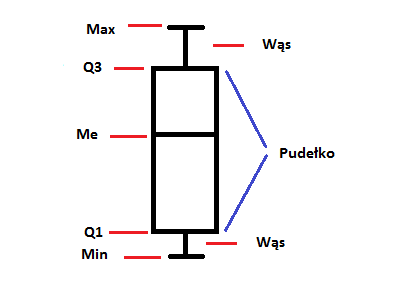
[[Plik:Wariant_prosty_AgnieszkaGalka.png|400px|right|thumb|Rys.1. Wariant prosty]] | * Q1 - kwartyl 1 | ||
Wąs to kreska, która łączy wartość minimalną (Min) i maksymalną (Max) z końcem pudełka. | * Min - wartość minimalna | ||
[[Informacje]] dotyczące prostego wariantu: | |||
* Długość pudełka równa się '''rozstępowi ćwiartkowemu''' ''<math>Q3-Q1</math>'' | [[Plik:Wariant_prosty_AgnieszkaGalka.png|400px|right|thumb|Rys.1. Wariant prosty]] | ||
* Wąsy mogą przybierać różną długość, w zależności od tego, ile wynosi wartość maksymalna i minimalna | |||
* Mediana nie zawsze leży pośrodku pudełka | Wąs to kreska, która łączy wartość minimalną (Min) i maksymalną (Max) z końcem pudełka. | ||
'''Wariant złożony''' | |||
W tym przypadku do zbudowania wykresu pudełkowego potrzebujemy: | [[Informacje]] dotyczące prostego wariantu: | ||
* Q3- kwartyl 3 | * Długość pudełka równa się '''rozstępowi ćwiartkowemu''' ''<math>Q3-Q1</math>'' | ||
* Me- mediana | * Wąsy mogą przybierać różną długość, w zależności od tego, ile wynosi wartość maksymalna i minimalna | ||
* Q1- kwartyl 1 | * Mediana nie zawsze leży pośrodku pudełka | ||
*IQR- rozstęp ćwiartkowy, wyliczany następująco: | |||
<math>IQR= Q3- Q1 </math> | '''Wariant złożony''' | ||
Wąsy wyznaczane są następująco: | |||
<math>Min= Q1- 1.5*IQR</math> | W tym przypadku do zbudowania wykresu pudełkowego potrzebujemy: | ||
* Q3 - kwartyl 3 | |||
<math>Max= Q3+1.5*IQR</math> | * Me - mediana | ||
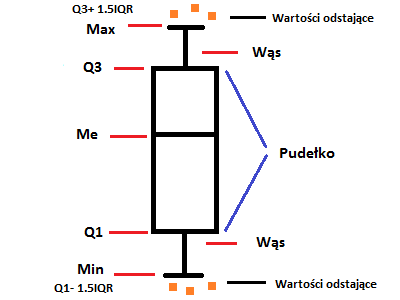
[[Plik:Wariant_zlozony_AgnieszkaGalka.png|400px|right|thumb|Rys.2. Wariant złożony]] | * Q1 - kwartyl 1 | ||
W przypadku, gdy jakieś wartości znajdują się poniżej Min lub powyżej Max, obrazuje się je na wykresie jako gwiazdki. Są to wartości, które reprezentują '''wartości odstające''', to znaczy takie, które zdecydowanie odbiegają od reszty. | * IQR - rozstęp ćwiartkowy, wyliczany następująco: | ||
Informacje dotyczące wariantu złożonego: | |||
* Długość pudełka równa się rozstępowi ćwiartkowemu <math>Q3-Q1</math | <math>IQR= Q3 - Q1 </math> | ||
* Wąsy mają identyczną długość | |||
* Mediana nie zawsze leży na środku pudełka | Wąsy wyznaczane są następująco: | ||
* Wykres ten służy do lokalizowania wartości odstających, które mogą w zasadniczy sposób zaburzać interpretację wyników | |||
<math>Min= Q1-1.5*IQR</math> | |||
<math>Max= Q3+1.5*IQR</math> | |||
[[Plik:Wariant_zlozony_AgnieszkaGalka.png|400px|right|thumb|Rys.2. Wariant złożony]] | |||
W przypadku, gdy jakieś wartości znajdują się poniżej Min lub powyżej Max, obrazuje się je na wykresie jako gwiazdki. Są to wartości, które reprezentują '''wartości odstające''', to znaczy takie, które zdecydowanie odbiegają od reszty. | |||
Informacje dotyczące wariantu złożonego: | |||
* Długość pudełka równa się rozstępowi ćwiartkowemu <math>Q3-Q1</math> | |||
* Wąsy mają identyczną długość | |||
* Mediana nie zawsze leży na środku pudełka | |||
* Wykres ten służy do lokalizowania wartości odstających, które mogą w zasadniczy sposób zaburzać interpretację wyników (K. Potter 2006, s.98-100) | |||
==Analiza wykresu== | ==Analiza wykresu== | ||
*'''Położenie'''- położenie obrazuje cały wykres pudełkowy (wartości min i max); | * '''Położenie''' - położenie obrazuje cały wykres pudełkowy (wartości min i max); | ||
*'''Rozproszenie'''- im wykres jest dłuższy, tym [[dane]] są bardziej rozsiane, co oznacza, że mogą przyjmować zróżnicowane wartości. O rozproszeniu informują też długie wąsy- świadczą one o występowaniu obserwacji skrajnych- znacząco oddalonych od pudełka; | * '''Rozproszenie''' - im wykres jest dłuższy, tym [[dane]] są bardziej rozsiane, co oznacza, że mogą przyjmować zróżnicowane wartości. O rozproszeniu informują też długie wąsy- świadczą one o występowaniu obserwacji skrajnych - znacząco oddalonych od pudełka; | ||
*'''Kształt'''- jeżeli wykres wydaje się symetryczny względem kreski z medianą, to można przyjąć [[założenie]], że wykres badanej cechy jest '''symetryczny'''. W przypadku, gdy pudełko nie jest równo podzielone albo/i wąsy mają różną długość mamy do czynienia z '''asymetrią''' ([[prawo]]- lub lewostronną, co odczytuje się po odległości Min i Max od Mediany) i wykres cechy jest '''rozkładem asymetrycznym'''; (J. Łuczak 2007, s.258) | * '''Kształt''' - jeżeli wykres wydaje się symetryczny względem kreski z medianą, to można przyjąć [[założenie]], że wykres badanej cechy jest '''symetryczny'''. W przypadku, gdy pudełko nie jest równo podzielone albo/i wąsy mają różną długość mamy do czynienia z '''asymetrią''' ([[prawo]] - lub lewostronną, co odczytuje się po odległości Min i Max od Mediany) i wykres cechy jest '''rozkładem asymetrycznym'''; (J. Łuczak 2007, s.258) | ||
==Interpretacja== | ==Interpretacja== | ||
Z wykresu odczytujemy następujące własności: | Z wykresu odczytujemy następujące własności: | ||
| Linia 83: | Linia 93: | ||
* Występowanie nietypowych wariantów cechy | * Występowanie nietypowych wariantów cechy | ||
* Pojawienie się ekstremalnych wariantów cechy | * Pojawienie się ekstremalnych wariantów cechy | ||
==Zalety== | ==Zalety== | ||
Wykres pudełkowy w bardzo łatwy sposób pozwala ilustrować nawet '''duże ilości danych''' i przejrzyście obrazuje '''wartości odstające'''. (J. Łuczak 2007 s.257) | Wykres pudełkowy w bardzo łatwy sposób pozwala ilustrować nawet '''duże ilości danych''' i przejrzyście obrazuje '''wartości odstające'''. (J. Łuczak 2007 s.257) | ||
==Wady== | ==Wady== | ||
Wykres pudełkowy nie ma nadaje się do szczegółowej analizy danych, ponieważ prezentuje jedynie '''sumaryczny rozkład wartości'''. (J. Łuczak 2007, s.257) | Wykres pudełkowy nie ma nadaje się do szczegółowej analizy danych, ponieważ prezentuje jedynie '''sumaryczny rozkład wartości'''. (J. Łuczak 2007, s.257) | ||
==Zastosowanie== | ==Zastosowanie== | ||
* Zdefiniowanie rozproszenia danej cechy. | * Zdefiniowanie rozproszenia danej cechy. | ||
| Linia 92: | Linia 105: | ||
* Ułatwia diagnostykę typu skośności rozkładu cechy. | * Ułatwia diagnostykę typu skośności rozkładu cechy. | ||
* Wspomaga analizy, interpretacje danych statystycznych. | * Wspomaga analizy, interpretacje danych statystycznych. | ||
* Z diagramów pudełkowych korzysta się przy porównaniu rozkładów dwóch lub więcej [[Zmienna|zmiennych]]. | * Z diagramów pudełkowych korzysta się przy porównaniu rozkładów dwóch lub więcej [[Zmienna|zmiennych]]. | ||
{{infobox5|list1={{i5link|a=[[Histogram]]}} — {{i5link|a=[[Kwartyl]]}} — {{i5link|a=[[Współczynnik determinacji]]}} — {{i5link|a=[[Metody statystyczne]]}} — {{i5link|a=[[Analiza regresji]]}} — {{i5link|a=[[Rozkład normalny]]}} — {{i5link|a=[[Percentyl]]}} — {{i5link|a=[[Wykres słupkowy]]}} — {{i5link|a=[[Krzywa wzorcowa]]}} }} | |||
==Bibliografia== | ==Bibliografia== | ||
<noautolinks> | <noautolinks> | ||
* Łuczak J. (2007) | * Łuczak J. (2007), ''Metody i techniki zarządzania jakością'', Quality Progress, Poznań | ||
* Malarska A. (2005) | * Malarska A. (2005), ''Statystyczna analiza danych'', SPSS Polska, Kraków | ||
* Nowak-Brzezińska A. (2011) | * Nowak-Brzezińska A. (2011), ''Przygotowywanie danych w środowisku R'', Uniwersytet Śląski w Katowicach, Katowice | ||
* Poniat R. (2014) | * Poniat R. (2014), ''O wykorzystaniu wykresów pudełkowych do prezentacji danych demograficznych i o pożytku z użycia środowiska R z pakietem ggplot2'', Przyszłość demograficzna Polski, nr 34 | ||
* Potter K. (red.) (2006) | * Potter K. (red.) (2006), ''Methods for presenting statistical information: The box plot'', Visualization of large and unstructured data sets, nr 4 | ||
* Trzęsiok M. (2014) | * Trzęsiok M. (2014), ''[https://www.infona.pl/resource/bwmeta1.element.desklight-67e7183b-47b0-4da4-9cab-330d5d54992e/content/partDownload/bef9c9d5-5ef2-3334-9b7a-f85b0c012eb4 O jakości danych w kontekście obserwacji oddalonych w wielowymiarowej analizie regresji]'', Studia Ekonomiczne, nr 191 | ||
* Woch J. (2002) | * Woch J. (2002), ''Statystyka procesów transportowych'', Instytut Transportu Politechniki Śląskiej, Katowice | ||
</noautolinks> | </noautolinks> | ||
[[Kategoria:Prezentacja danych]] | |||
[[Kategoria: | |||
{{a|Wojciech Szpara, Agnieszka Gałka}} | {{a|Wojciech Szpara, Agnieszka Gałka}} | ||
{{#metamaster:description|Wykres pudełkowy, inaczej znany jako wykres skrzynkowy, umożliwia graficzną prezentację rozkładu statystycznego cechy. Zaproponowany przez Johna Tukeya, cechuje się przejrzystością i zwięzłością.}} | {{#metamaster:description|Wykres pudełkowy, inaczej znany jako wykres skrzynkowy, umożliwia graficzną prezentację rozkładu statystycznego cechy. Zaproponowany przez Johna Tukeya, cechuje się przejrzystością i zwięzłością.}} | ||
Aktualna wersja na dzień 20:33, 17 gru 2023
Wykres pudełkowy nazywany często wykresem skrzynkowym, ramkowym lub wykresem "ramka - wąsy" (z języka angielskiego - box plot). Jest jednym z narzędzi statystycznych metod zarządzania jakością. Wykresy pudełkowe opracowywane są w oparciu o wartości statystyk opisowych, dlatego ich zastosowanie ogranicza się do cech liczbowych. Stanowią prostą formę graficznej prezentacji rozkładu cechy statystycznej. Pozwalają na ujęcie na jednym rysunku wszystkich wiadomości, które dotyczą położenia, kształtu a także rozkładu empirycznego badanej cechy. Charakteryzuje je duża przejrzystość i zwięzłość. (M. Trzęsiok 2014, s.107)
Wykres został zaproponowany przez Johna Tukeya w książce "Explanatory Data Analysis", wydanej w 1997 roku. Tukey uważa, że wymyślony przez niego wykres ma duża wartość i pozwala na odkrycie czegoś, czego się nie spodziewaliśmy- "The gratest value of a picture is when it forces us to notice what we never expected to see".
TL;DR
Wykres pudełkowy, znany też jako wykres skrzynkowy, ramkowy lub ramka-wąsy, jest narzędziem statystycznym do prezentacji rozkładu cechy statystycznej. Składa się z prostokąta, osi współrzędnych i wąsów. Wykres ma formę minimalistyczną, ale przekazuje wiele informacji. Istnieją różne typy wykresów pudełkowych, najpopularniejszy to wykres z medianą, kwartylami i wartościami minimalną i maksymalną. Wykres pudełkowy jest używany do analizy rozproszenia i kształtu danych. Ma wiele zastosowań, m.in. w analizie danych statystycznych i porównywaniu rozkładów zmiennych.
Opis wykresu
Wykres składa się z prostokąta (pudełka), osi współrzędnych i tak zwanych wąsów, czyli odległości wartości minimalnej i maksymalnej od pudełka. Wykres ma formę minimalistyczną, ponieważ przedstawia tylko 5 informacji i chociaż wydaję się, że jest to niewiele, wykres ramka-wąsy przekazuje nam na bardzo dużo wiadomości. Najczęściej do jego sporządzenia musimy znać dokładne wartości: pierwszego i trzeciego kwartyla, mediany oraz minimum i maksimum. Dzięki tym danym możemy badać poziom rozproszenia danej czy odległości mediany od minimum i maksimum (J. Łuczak 2007, s.255-258) Długość prostokąta reprezentuje rozstęp ćwiartkowy IQR, obejmujący 50% środkowych obserwacji. Pudełko jest rozdzielone pionową linią, która wyznacza wartość mediany. Dzieli ona przedział ćwiartkowy na dwa obszary, w których znajduje się 25% obserwacji. Wąsy łączą pudełko z największą i najmniejszą wartością badanej zmiennej odpowiednio z przedziału (Q1-1,5*IQR; Q1) oraz (Q3; Q3+1,5 IQR). W pierwszym przedziale znajduje się 25% obserwacji o wartościach niższych od dolnego kwartyla a w drugim przedziale 25% obserwacji o wartościach wyższych od górnego kwartyla (A. Malarska 2005, s.26-27))
Typy wykresów pudełkowych
Wyróżnia się następujące typy wykresów pudełkowych:
1. Średnia/błąd standardowy/odchylenie standardowe
2. Mediana/kwartyle/minimum, maksimum
3. Średnia/odchylenie standardowe/minimum maksimum
4. Średnia/przedział ufności/odchylenie standardowe
Należy zaznaczyć, że najczęściej spotykanym typem jest nr 2.
Sporządzanie i charakterystyka wykresu pudełkowego
Aby sporządzić wykres należy:
- Narysować oś liczbową, na której odmierza się wartości badanej cechy.
- Umieścić wzdłuż osi pudełko (skrzynkę), którego lewy bok wyznacza wartość kwartyla 1, natomiast prawy bok - wartość kwartyla 3.
- Uzupełnić wykres dwoma odcinkami, które znajdują się na zewnątrz pudełka (tzw.: wąsy).
Wykres pudełkowy posiada dwa warianty:
- prosty - bazuje na głównych statystykach;
- złożony - używany do prezentacji wartości odstających, tzw. outlierów;
Wariant prosty
Do stworzenia prostego wykresu pudełkowego niezbędne jest 5 wartości:
- Max - wartość maksymalna
- Q3 - kwartyl 3
- Me - mediana
- Q1 - kwartyl 1
- Min - wartość minimalna
Wąs to kreska, która łączy wartość minimalną (Min) i maksymalną (Max) z końcem pudełka.
Informacje dotyczące prostego wariantu:
- Długość pudełka równa się rozstępowi ćwiartkowemu
- Wąsy mogą przybierać różną długość, w zależności od tego, ile wynosi wartość maksymalna i minimalna
- Mediana nie zawsze leży pośrodku pudełka
Wariant złożony
W tym przypadku do zbudowania wykresu pudełkowego potrzebujemy:
- Q3 - kwartyl 3
- Me - mediana
- Q1 - kwartyl 1
- IQR - rozstęp ćwiartkowy, wyliczany następująco:
Wąsy wyznaczane są następująco:
W przypadku, gdy jakieś wartości znajdują się poniżej Min lub powyżej Max, obrazuje się je na wykresie jako gwiazdki. Są to wartości, które reprezentują wartości odstające, to znaczy takie, które zdecydowanie odbiegają od reszty.
Informacje dotyczące wariantu złożonego:
- Długość pudełka równa się rozstępowi ćwiartkowemu
- Wąsy mają identyczną długość
- Mediana nie zawsze leży na środku pudełka
- Wykres ten służy do lokalizowania wartości odstających, które mogą w zasadniczy sposób zaburzać interpretację wyników (K. Potter 2006, s.98-100)
Analiza wykresu
- Położenie - położenie obrazuje cały wykres pudełkowy (wartości min i max);
- Rozproszenie - im wykres jest dłuższy, tym dane są bardziej rozsiane, co oznacza, że mogą przyjmować zróżnicowane wartości. O rozproszeniu informują też długie wąsy- świadczą one o występowaniu obserwacji skrajnych - znacząco oddalonych od pudełka;
- Kształt - jeżeli wykres wydaje się symetryczny względem kreski z medianą, to można przyjąć założenie, że wykres badanej cechy jest symetryczny. W przypadku, gdy pudełko nie jest równo podzielone albo/i wąsy mają różną długość mamy do czynienia z asymetrią (prawo - lub lewostronną, co odczytuje się po odległości Min i Max od Mediany) i wykres cechy jest rozkładem asymetrycznym; (J. Łuczak 2007, s.258)
Interpretacja
Z wykresu odczytujemy następujące własności:
- Położenie mediany
- Położenie kwartyli
- Wartości kwartyli:
- pierwszy kwartyl
- trzeci kwartyl
- Położenie wariantów cechy, które nie odstają od tendencji centralnej
- Występowanie nietypowych wariantów cechy
- Pojawienie się ekstremalnych wariantów cechy
Zalety
Wykres pudełkowy w bardzo łatwy sposób pozwala ilustrować nawet duże ilości danych i przejrzyście obrazuje wartości odstające. (J. Łuczak 2007 s.257)
Wady
Wykres pudełkowy nie ma nadaje się do szczegółowej analizy danych, ponieważ prezentuje jedynie sumaryczny rozkład wartości. (J. Łuczak 2007, s.257)
Zastosowanie
- Zdefiniowanie rozproszenia danej cechy.
- Ukazuje nam rozkład uporządkowanych wartości cechy.
- Ułatwia diagnostykę typu skośności rozkładu cechy.
- Wspomaga analizy, interpretacje danych statystycznych.
- Z diagramów pudełkowych korzysta się przy porównaniu rozkładów dwóch lub więcej zmiennych.
| Wykres pudełkowy — artykuły polecane |
| Histogram — Kwartyl — Współczynnik determinacji — Metody statystyczne — Analiza regresji — Rozkład normalny — Percentyl — Wykres słupkowy — Krzywa wzorcowa |
Bibliografia
- Łuczak J. (2007), Metody i techniki zarządzania jakością, Quality Progress, Poznań
- Malarska A. (2005), Statystyczna analiza danych, SPSS Polska, Kraków
- Nowak-Brzezińska A. (2011), Przygotowywanie danych w środowisku R, Uniwersytet Śląski w Katowicach, Katowice
- Poniat R. (2014), O wykorzystaniu wykresów pudełkowych do prezentacji danych demograficznych i o pożytku z użycia środowiska R z pakietem ggplot2, Przyszłość demograficzna Polski, nr 34
- Potter K. (red.) (2006), Methods for presenting statistical information: The box plot, Visualization of large and unstructured data sets, nr 4
- Trzęsiok M. (2014), O jakości danych w kontekście obserwacji oddalonych w wielowymiarowej analizie regresji, Studia Ekonomiczne, nr 191
- Woch J. (2002), Statystyka procesów transportowych, Instytut Transportu Politechniki Śląskiej, Katowice
Autor: Wojciech Szpara, Agnieszka Gałka