Diagram Venna: Różnice pomiędzy wersjami
m (cleanup bibliografii i rotten links) |
m (cleanup bibliografii i rotten links) |
||
| Linia 52: | Linia 52: | ||
<noautolinks> | <noautolinks> | ||
* Andrzejaczak G. (1997), ''Encyklopedia szkolna. Matematyka'', Wydawnictwa Szkolne i Pedagogiczne, Warszawa | * Andrzejaczak G. (1997), ''Encyklopedia szkolna. Matematyka'', Wydawnictwa Szkolne i Pedagogiczne, Warszawa | ||
* Guzicki W., Zakrzewski P. | * Guzicki W., Zakrzewski P. (2005), ''Wstęp do matematyki. Wprowadzenie do teorii mnogości'', PWN, Warszawa | ||
* Kulpa Z. (2006), ''[https://www.ippt.pan.pl/Repository/o128.pdf Koła Eulera i diagramy Venna, czyli jaka jest różnica między kanarkiem?]'' | * Kulpa Z. (2006), ''[https://www.ippt.pan.pl/Repository/o128.pdf Koła Eulera i diagramy Venna, czyli jaka jest różnica między kanarkiem?]'' | ||
* Tarski A. (2012), ''[https://www.calculemus.org/tarski-wprowadzenie/tarski.pdf Wprowadzenie do logiki i do metodologii nauk dedukcyjnych]'', PHILOMATH, Warszawa | * Tarski A. (2012), ''[https://www.calculemus.org/tarski-wprowadzenie/tarski.pdf Wprowadzenie do logiki i do metodologii nauk dedukcyjnych]'', PHILOMATH, Warszawa | ||
Aktualna wersja na dzień 20:38, 5 sty 2024
Diagram Venna wykorzystuje nachodzące na siebie koła lub inne kształty, aby pokazać logiczne zależności pomiędzy dwoma lub więcej zestawami elementów. Często używa się go do graficznego porządkowania rzeczy, zaznaczając, że elementy są podobne lub różnią się od siebie.
Diagramy Venna zwane również schematami zestawów lub diagramami logicznymi, stosowane są szeroko w matematyce, statystyce, logistyce, nauczaniu, informatyce i biznesie. Większa część z nas spotyka diagramy Venna spotyka się w czasie nauki matematyki, ponieważ stały się one częścią programów nauczania nowej matematyki w latach sześćdziesiątych. Są używane do pokazania w jaki sposób przedmioty odnoszą się do każdego z określonych wszechświatów lub segmentów. Diagramy Venna umożliwiają użytkownikom wizualizację danych w jasny i skuteczny sposób dzięki czemu są stosowane powszechnie we wszelkiego rodzaju prezentacjach i raportach. Schematy te są ściśle powiązane ze schematami Eurela. Schematu Eurela różnią się tyk że pomijają zbiory, jeśli nie ma w nich żadnych elementów, natomiast diagramy Venna pokazują związki nawet jeśli zbiór jest pusty. Rys. 1 [1]
TL;DR
Diagramy Venna są używane do pokazywania zależności między zestawami elementów. Są wykorzystywane w matematyce, statystyce, logice, nauczaniu, informatyce i biznesie. Przykładem jest diagram przedstawiający preferencje zwierząt domowych. Diagramy Venna mają wiele zastosowań, w tym w matematyce, statystyce, logice, językoznawstwie, nauczaniu czytania ze zrozumieniem, informatyce i biznesie. Są one używane do wizualizacji danych, rozwiązywania problemów matematycznych, porównywania wyborów i analizowania danych.
Przykład Diagramu Venna
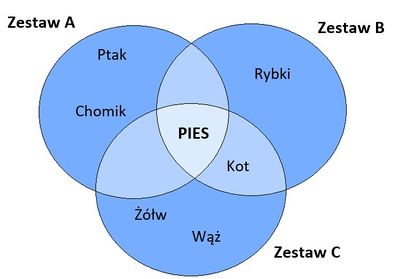
Załóżmy, że nasz wszechświat to zwierzęta domowe. Chcemy się dowiedzieć do z jaką rodziną zwierząt zgodzi się nasz zbiór (jakie zwierzęta domowe są najbardziej popularne).
- Zestaw A: zawiera moje preferencje: pies, ptak, chomik,
- Zestaw B: zawiera preferencje znajomego 1: pies, kot, rybki,
- Zestaw C: zawiera preferencje znajomego 2: pies, kot, żółw, wąż.
Po nałożeniu 3 zestawów część wspólna zawiera tylko Psa. Wynika z tego, że najczęściej wybieranymi (najpopularniejszymi) zwierzętami domowymi są psy.
Oczywiście diagramy Venna mogą być o wiele bardziej zaawansowane. Rys. 2 [2]
Cel i korzyści
- wizualne uporządkowanie informacji. Wykazanie związków między zestawami elementów. Profesjonalnie wykorzystywane, by przemyśleć logikę stojąca za koncepcją i przedstawić relację między nimi,
- rozwiązywanie złożonych problemów matematycznych,
- porównanie dwóch lub więcej wyborów. Możemy wyraźnie pokazać w czym się różnią i co je łączy. Dzięki czemu łatwiej nam jest dokonać wyboru produktu bądź usługi
- porównanie zestawów danych odszukanie korelacji oraz przewidzenie prawdopodobieństwa wystąpienia pewnych zdarzeń,
- rozumowanie zapomogą instrukcji lub równań logicznych, takich jak logika Boole’a wyszukującą "lub" i "i" oraz sposób ich grupowania.
Zastosowanie
Matematyka: powszechnie używane w szkole do uczenia podstawowych pojęć matematycznych, np. zbiory, związki. Są także używane w matematyce zaawansowane, aby rozwiązać ciężkie i czasochłonnych założeń, Szeroko opisane w czasopismach naukowych jako teoria mnogości.
Statystyka i prawdopodobieństwo: eksperci wykorzystują te schematy do przewidywania prawdopodobieństwa wystąpienia zdarzeń. Wiąże się to z polem analizy predykcyjnej. Różne zestawy danych można porównywać w celu znalezienia stopnia podobieństwa oraz zróżnicowania.
Logika: diagramy Venna służą dookreślenia ważności poszczególnych argumentów i wniosków. W rozumieniu dedukcyjnym, jeśli przesłanki są prawdziwe, a formularz argumentu jest poprawny, wynik musi być prawdziwy. Np. wszystkie koty są zwierzętami, Mruczek jest kotem z tego wynika ze Mruczek jest zwierzęciem. W formie oficjalnie mówimy, że wszystkie A to B. C to A, dlatego C to B. Powiązane diagramy w logice nazywamy Tabelami prawdy, w których umieszczę się zmienne w kolumnach w celu ustalenia co jest logicznie prawdziwe.
Językoznawstwo: diagramy pomagają badań podobieństwo i różnice między językami.
Nauczanie czytania ze zrozumieniem: nauczyciele mogą wykorzystywać diagramy Venna, by poprawić rozumienie tekstów przez swoich małych studentów. Uczniowie mogą rysować diagramy, aby lepiej zapamiętywać powiązania w długich tekstach.
Informatyka: Programiści wykorzystują diagramy do wizualizacji języków programowania i hierarchii.
Biznes: schematy Venna mogą być użyte do zestawiania produktów, usług, procesów i wielu innych, Można to pokazać na zestawach, są skutecznym narzędziem komunikacji, aby zilustrować to równanie[3]
| Diagram Venna — artykuły polecane |
| Fuzzy logic — Data science — Wzorce projektowe — Ontologia — Bioinformatyka — Hipoteza — Analiza danych — Wykres kołowy — Diagram macierzowy |
Przypisy
Bibliografia
- Andrzejaczak G. (1997), Encyklopedia szkolna. Matematyka, Wydawnictwa Szkolne i Pedagogiczne, Warszawa
- Guzicki W., Zakrzewski P. (2005), Wstęp do matematyki. Wprowadzenie do teorii mnogości, PWN, Warszawa
- Kulpa Z. (2006), Koła Eulera i diagramy Venna, czyli jaka jest różnica między kanarkiem?
- Tarski A. (2012), Wprowadzenie do logiki i do metodologii nauk dedukcyjnych, PHILOMATH, Warszawa
- Wieczorek K. (2002), Wszystko co powinniście wiedzieć o logice, ale nie uważaliście na zajęciach, Logika dla opornych
Autor: Martyna Sołtys