Histogram

Histogram to zestawienie danych statystycznych w postaci wykresu powierzchniowego złożonego z przylegających do siebie słupków (prostokątów), których wysokość ilustruje liczebność występowania badanej cechy w populacji lub jej próbie , a podstawy (które spoczywają na osi odciętych) są rozpiętościami przedziałów klasowych.

TL;DR

Histogram to wykres statystyczny, który ilustruje częstość występowania danej cechy w populacji lub próbie. Jest ważnym narzędziem do analizy jakości i umożliwia lepsze zrozumienie badanego zjawiska. Histogramy są stosowane głównie do przedstawienia struktury zbiorowości i mogą mieć różne typy, takie jak podstawowy, grzebieniowy, asymetryczny, jednostronny, kopców, siodła, z izolowanym pagórkiem i bez wartości skrajnych. Przygotowanie histogramu wymaga zebrania wyników pomiarowych, ustalenia ilości przedziałów i obliczenia szerokości przedziałów.

Zastosowanie

Histogram ma zastosowanie również w dziedzinie statystyki służy do graficznego zaprezentowania częstości występowania zmiennej losowej w danym przedziale, zaś jeśli chodzi o analizę jakości ten rodzaj wykresu ma za zadanie wizualizację zmienności co w dalszych etapach ułatwia podjęcie decyzji dotyczących usprawnienia działań i poprawy jakości badanego obiektu . Wspomniany rodzaj wykresu jest uważany jako jeden z siedmiu podstawowych narzędzi, które służą do doskonalenia jakości o bardzo szerokim zastosowaniu. Za jego pomocą możliwe jest graficzne przestawienie rozkładu badanej cechy, a w konsekwencji umożliwia lepsze zrozumienie analizowanego zjawiska .

Ułatwia identyfikacje jakiego rodzaju jest rozkład ciągły prawdopodobieństwa, który służy do prognozowania. Zadaniem wymienionej techniki jest eliminowanie ewentualnych wad, ostrzeżenie przed potencjalnymi trudnościami z zakresu jakości przed ich liczniejszym wystąpieniem .

Taki sposób konstrukcji histogramu jest stosowany wówczas, kiedy przedziały szeregu rozdzielczego są równe.Jeżeli szereg ma nierówne przedziały, to wysokość prostokątów jest określona przez wskaźniki natężenia liczebności (częstości) odpowiadające poszczególnym klasom.

Ustalenie wskaźników liczebności

Wskaźniki liczebności (częstości) ustala się w następujący sposób:

wskaźnik $_{\text{natezenia}}$ =${\frac {k*i}{l}}$

gdzie:

k - to liczebność danej klasy

i - to interwał klasy najwęższej

l - to interwał danej klasy

Histogramy są stosowane głównie dla przedstawienia struktury zbiorowości (lub zjawiska),

a więc szeregów strukturalnych dotyczących cech jakościowych i ilościowych.

Wykresy podkreślające podstawowe cechy danej zbiorowości (lub zjawiska) muszą być precyzyjnie dostosowane do charakteru

tychże cech. Tak więc opisując przykładowo rozkład studentów według liczby dni spędzonych na nauce w danym okresie

czy rozkład zatrudnionych według liczby dni nie przepracowanych z powodu choroby w danym okresie

sporządzimy histogram. Nie możemy natomiast posłużyć się tym wykresem do opisania tendencji rozwojowej,

wahań sezonowych i przypadkowych (gdzie zaleca się stosowanie krzywej dynamiki)

czy opisania współzależności (którą należy przedstawić na wykresie korelacji).

Budowa histogramu

Histogram podobnie jak pozostałe wykresy statystyczne składa się z kilku części:

• pola
• wykresu
• skali (aby ułatwić czytanie wykresu, stosuje się nieraz, zwłaszcza w prostokątnym układzie współrzędnych, dwie jednakowe skale na obu krańcach obrazu graficznego,

tj skalę poziomą oraz dwie skale pionowe po lewej i po prawej stronie pola wykresu)

• tytułu (w wykresach popularyzacyjnych tytuł należy umieścić nad obrazem graficznym, natomiast w publikacjach można go umieścić również pod rysunkiem)
• legendy
• źródła (jeżeli obok wykresu w tej samej publikacji zamieszczamy tablicę statystyczną z danymi liczbowymi i opatrzona jest ona opisem źródła informacji, wystarczy pod wykresem wymienić jako źródło numer kolejny tej tablicy) i innych objaśnień.

Podstawą sporządzania histogramu opisującego prawidłowości występujące w zbiorowościach (zjawiskach)

jest układ współrzędnych prostokątnych, przy czym główną uwagę należy skupić na doborze skali

i precyzyjnym obrazie graficznym, a nie na opisie wykresu i jego atrakcyjności.

Szczególną postacią histogramu jest 'histogram kumulacyjny'. Na osi odciętych w prostokątnym układzie

współrzędnych odkłada się wówczas liczebności skumulowane .

Jak przygotować histogram

Przygotowanie histogramu składa się z kilku etapów tj:

1. Zebranie wyników pomiarowych
   1. Należy pamiętać, aby odbrać próbkę w sposób losowy
   2. Upewnić się, że metoda pomiaru danej cechy jest poprawna
2. Ustalenie ilości przedziałów (klas)
   1. liczba klas (k) zależy od liczebności badanej zbiorowości (n) i w przybliżeniu ustalamy ją jako: $k={\sqrt {n}}$
3. Obliczenie szerokości przedziałów
   1. Rozpiętość przedziałów ustalamy na podstawie różnicy między najwyższą ($x_{\text{max}}$ i najniższą $x_{\text{min}}$)

wartością cechy (tzw. rozstęp), podzielonej przez liczbą klas:

$c={\frac {\left(x_{\text{max}}-x_{\text{min}}\right)}{k}}$

Szereg jest zawsze bardziej przejrzysty, jeżeli możliwe jest przyjęcie rozpiętości przedziałów w postaci liczby 5, 10, 50, 100 itd.

1. Ustalenie dolnej granicy pierwszego przedziału jako:

$x_{i}0=x_{\text{min}}-{\frac {c}{2}}$,

stąd $x_{\text{min}}$ znajdzie się w środku pierwszego przedziału.

1. określenie ilości obserwacji w danym przedziale

W przypadku nierównych przedziałów klasowych przy konstruowaniu histogramu należy pamiętać

o następujących zasadach:

• na osi przedziałów klasowych odkładamy szerokości poszczególnych kolumn proporcjonalnie do rozpiętości przedziału klasowego,
• wysokości kolumn zmniejszamy lub zwiększamy w stosunku odwrotnie proporcjonalnym do stopnia zmniejszenia lub zwiększenia

szerokości kolumn .

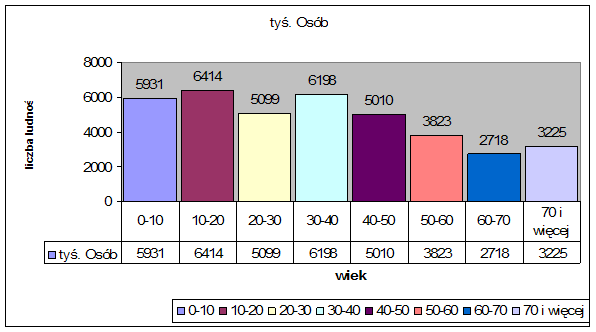
Przykładowy histogram

Rys. 1. Przykład histogramu

źródło: opracowanie własne na podstawie danych Rocznika statystycznego GUS 1993, s. 46

Typy histogramów

Kształt histogramu jest kluczowym elementem bowiem podkreśla rodzaj informacji bądź zaburzeń. Wyróżniamy kilka rodzajów histogramów :

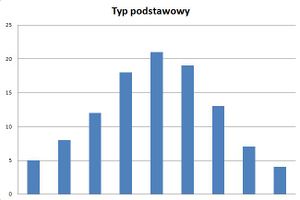
• Typ podstawowy - charakteryzuje się systematycznym kształtem przypominającym zarys dzwonu,
  

  Rys. 2 Typ podstawowy
  a jego wartość średnia znajduje się w centralnej jego części. Ten typ sugerować może rozkład normalny, a w konsekwencji prawdopodobnie występowanie jednej przyczyny, która wpływa na jego zmienność.
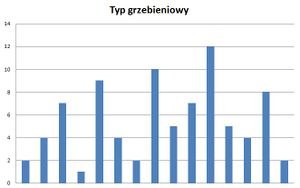
• Typ grzebieniowy - z tego typu wykresem mamy do czynienia gdy nie ma wyraźnego jednego wzniesienia,
  

  Rys. 3 Typ grzebieniowy
  lecz wysokości danych słupków są naprzemiennie duże bądź małe przypominające kształtem grzebień. Taka różnorodność ich wysokości może świadczyć o występowaniu kilku przyczyn zmienności histogramu.
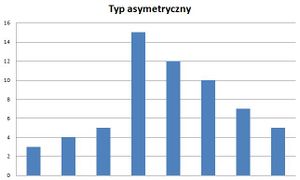
• Typ asymetryczny - charakteryzuje go występowanie wartości średniej wyraźnie po jednej
  

  Rys. 4 Typ asymetryczny
  ze stron rozkładu, w której skupia się większość obserwacji. Ten histogram ma miejsce wtedy gdy chcemy utrzymać dolną bądź górną granicę tolerancji (może być wyznaczona odgórnie lub określona teoretycznie).
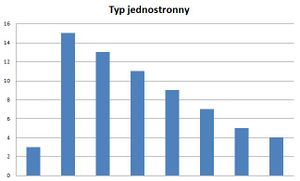
• Typ jednostronny - cechuje się tym iż wartość średnia znajduje się w przedziale granicznym.
  

  Rys. 5 Typ jednostronny
  Podkreśla wytypowanie bądź eliminację wartości, które znajdują się ponad bądź poniżej pewnej granicy.
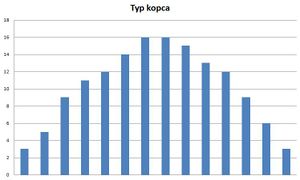
• Typ kopca - charakteryzuje się skupieniem zbliżonych częstości w przedziałach
  

  Rys. 6 Typ kopca
  znajdujących się pośrodku oraz spadających ich wartości bliżej granic danego rozkładu. Taki histogram świadczy o występowaniu kilku podobnych co do wartości zbiorów, które posiadają różniące się wartości średnie.
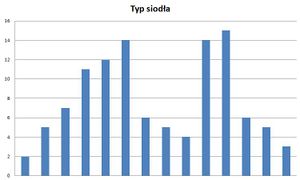
• Typ siodła - występują tu dwie wartości modalne (dominanty, mody), czyli wartości najczęstsze.
  

  Rys. 7 Typ siodła
  Przedstawia połączenie dwóch rozkładów posiadających odmienne wartości średnich i przedstawia odchylenia, które są łatwe w zidentyfikowaniu.
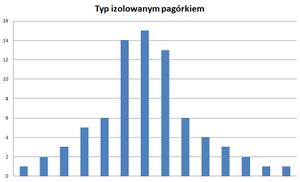
• Typ z izolowanym pagórkiem - najczęściej występuje w przypadku zmieszania różnych
  

  Rys. 8 Typ z izolowanym pagórkiem
  rozkładów o odmiennych parametrach. Charakterystyczny jest dla niego "pagórek" znacznie wyższy od pozostałości słupków i wyróżniający się na tle całego wykresu.
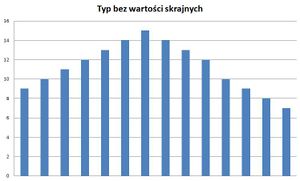
• Typ bez wartości skrajnych - z tym typem wykresu możemy się spotkać, gdy poprzednia
  

  Rys. 9 Typ bez wartości skrajnych
  selekcja innego rozkładu już się odbyła i zostały usunięte w niej wartości skrajne .

Histogram — artykuły polecane

Wykres słupkowy — Metody statystyczne — Analiza regresji — Kwartyl — ANOVA — Rozkład normalny — Skala porządkowa — Wykres pudełkowy — Analiza przyczynowa

Bibliografia

• Detyna B. (2011). Zarządzanie jakością w logistyce, Wydawnictwo Państwowej Szkoły Zawodowej im. Angelusa Silesiusa, Wałbrzych
• Dykiel M. Znaczenie wybranych narzędzi w zarządzaniu jakością
• Frąś J. (2011). Metody i techniki zarządzania jakością "Zeszyty naukowe Uniwersytetu Szczecińskiego Finanse, Rynki Finansowe, Ubezpieczenia", nr 46
• Kocimowski K. Kwiatek J. (1976). Wykresy i mapy statystyczne, GUS, Warszawa
• Krzysztofiak M., Luszniewicz A. (1976), Statystyka, PWE, Warszawa
• Siwek E. (2002), Słownik encyklopedyczny, Cykada, Katowice
• Sobczyk M. (2007), Statystyka, Wydawnictwo Naukowe PWN, Warszawa
• Wiśniewska M. (2014), Zarządzanie jakością i innowacyjność w świetle doświadczeń organizacji Pomorza, InnoBaltica, Gdańsk
• Zając K. (1994), Zarys metod statystycznych, Wydawnictwo PWE, Warszawa

Autor: Bernadeta Nowacka, Karolina Walczyk