Wykres słupkowy: Różnice pomiędzy wersjami
m (cleanup bibliografii i rotten links) |
m (cleanup bibliografii i rotten links) |
||
| Linia 61: | Linia 61: | ||
* Maksimowicz-Ajchel A.,(2007) ''Wstęp do statystyki. Metody opisu statystycznego'', Wyd. Uniwersytetu Warszawskiego, Warszawa | * Maksimowicz-Ajchel A.,(2007) ''Wstęp do statystyki. Metody opisu statystycznego'', Wyd. Uniwersytetu Warszawskiego, Warszawa | ||
* Paradysz J., (2005) ''Statystyka'', Wydawnictwo Akademii Ekonomicznej w Poznaniu, Poznań | * Paradysz J., (2005) ''Statystyka'', Wydawnictwo Akademii Ekonomicznej w Poznaniu, Poznań | ||
* Roeske-Słomka I. | * Roeske-Słomka I. (2010), ''Statystyka opisowa'', Wydawnictwo Uniwersytetu Ekonomicznego w Poznaniu, Poznań | ||
* Starzyńska W. (2004), ''Podstawy statystyki'', Difin, Warszawa | * Starzyńska W. (2004), ''Podstawy statystyki'', Difin, Warszawa | ||
* Zeliaś A. (2001), ''Metody statystyczne'', Polskie Wydawnictwo Ekonomiczne, Warszawa | * Zeliaś A. (2001), ''Metody statystyczne'', Polskie Wydawnictwo Ekonomiczne, Warszawa | ||
Wersja z 21:01, 11 lis 2023
| Wykres słupkowy |
|---|
| Polecane artykuły |
Wykres słupkowy (ang. bar chart, bar graph) - jedna z graficznych możliwości przedstawiania i prezentacji danych statystycznych. Należy do grupy wykresów powierzchniowych, które mają postać figur płaskich, zazwyczaj prostokątów (słupków). Stosuje się je do ilustracji struktury szeregów strukturalnych, przedziałowych, przestrzennych i czasowych. Wykresy słupkowe mają postać prostokątów (słupków) równoległych do siebie. Każdy z prostokątów przedstawia liczebność danego wariantu cechy. Im liczniej reprezentowany jest dany wariant cechy w zbiorowości, tym wyższy będzie słupek odpowiadający temu wariantowi. Za pomocą prostokątów (słupków) w dwuwymiarowym układzie kartezjańskim pokazuje się ilościowe dane, które służą albo ukazaniu struktury danego zjawiska (np. odsetek osób głosujących na daną partię polityczną), albo zmiany danej cechy statystycznej w czasie (np. dynamika sprzedaży w określonych latach). Wykres słupkowy używamy przy prezentacji badanej zbiorowości zarówno ze względu na cechę ilościową (mierzalną), jak i jakościową (niemierzalną). Używany jest jako podstawowa forma prezentacji.
Zastosowanie wykresu słupkowego
- Inną formą wykresu słupkowego jest wykres kolumnowy, który może przybrać formę poziomych słupków, równoległych względem siebie, o długościach odpowiadających wielkości zjawiska.
- Wykres słupkowy w zależności od zastosowania liczebności absolutnych lub względnych do ich sporządzania zwracają uwagę na wielkość lub na strukturę badanego zjawiska[1]
- Używany jest jako podstawowa forma prezentacji.
- Wykres słupkowy niekiedy zwany jest histogramem[2].
Zaś każdy histogram jest wykresem słupkowym, pozwala on ukazać strukturę rozkładu, gdyż dysproporcje pól wykreślanych prostokątów odzwierciadlają dysproporcje w liczebności rozkładu[3]
- Słupki (zarówno poziome jak i pionowe) najczęściej używane są w sytuacjach, gdy nie jest istotne jaki jest procentowy udział danych zaliczonych do poszczególnych kategorii w całości[4]
- Wykresy słupkowe konstruowane są niemal wyłącznie z użyciem skali arytmetycznej[5]
Historia wykresu słupkowego
Pierwszy raz w historii, wykres słupkowy został użyty przez Williama Playfaira w 1786 roku w "The Commercial and Political Atlas" Ukazywał on wielkość importu oraz eksportu pomiędzy Szkocją a jej partnerami handlowymi.
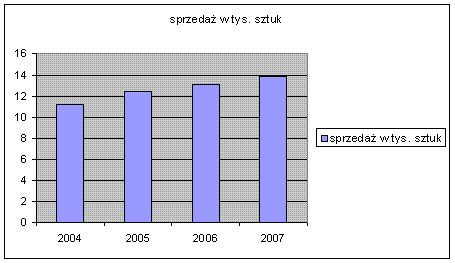
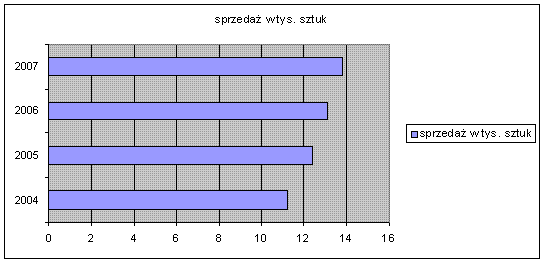
Przykłady wykresów słupkowych poniżej.
Rys. 2. Wykres słupkowy
W arkuszu kalkulacyjnym Ms Excel wykres słupkowy traktowany jest jako 2 odrębne kategorie: wykres słupkowy (słupki poziome) i kolumnowy (słupki pionowe). Co więcej arkusz ten pozwala stworzyć wykres słupkowy, gdzie zamiast prostokątów występują prostopadłościany.
Zgodnie z teorią statystyki słupki muszą być dwuwymiarowe (być prostokątami), ich układ z kolei (poziomy lub pionowy) jest dowolny. Wykres, w którym słupki są trójwymiarowe określa się mianem wykresu bryłowego [6]
Wymagania wykresu
Każdy wykres powinien posiadać tytuł oraz źródło, a także zawierać legendę, czyli objaśnienie znaków, barw, skali czy sposobu kreskowania użytych na wykresie. Tytuł wykresu powinien zwięźle informować o przedmiocie, czasie i miejscu przedstawionego graficznie zjawiska. Pod wykresem należy podać źródło, na podstawie którego go sporządzono.Forma wykresu zależy zawsze od rodzaju szeregu statystycznego, oraz od charakteru prawidłowości które ma on ilustrować.
Przypisy
- ↑ (Dominika Dusza (2010), Podstawy statystyki dla studentów administracji, Bielsko Biała)
- ↑ (Maksymowicz-Ajchel A., (2007) "Wstęp do statystyki. Metody opisu statystycznego", s. 35)
- ↑ (Maksymowicz-Ajchel A., (2007) "Wstęp do statystyki. Metody opisu statystycznego", s. 35)
- ↑ (A. Aczel (2000), "Statystyka w zarządzaniu" s. 39)
- ↑ (A. Zeliaś (2000), "Metody statystyczne" s. 31)
- ↑ (A. Bielecka 2001,"Statystyka w zarządzaniu - opis statystyczny" s. 54)
Bibliografia
- Aczel A. (2018), Statystyka w zarządzaniu, Wydawnictwo Naukowe PWN, Warszawa
- Bielecka A. (2001), Statystyka w zarządzaniu - opis statystyczny, Wydawnictwo WSPiZ im. L. Koźmińskiego, Warszawa
- Dusza D.,(2010) Podstawy statystyki dla studentów administracji, Wydawnictwo Wyższa Szkoła Administracji w Bielsku Białej
- Maksimowicz-Ajchel A.,(2007) Wstęp do statystyki. Metody opisu statystycznego, Wyd. Uniwersytetu Warszawskiego, Warszawa
- Paradysz J., (2005) Statystyka, Wydawnictwo Akademii Ekonomicznej w Poznaniu, Poznań
- Roeske-Słomka I. (2010), Statystyka opisowa, Wydawnictwo Uniwersytetu Ekonomicznego w Poznaniu, Poznań
- Starzyńska W. (2004), Podstawy statystyki, Difin, Warszawa
- Zeliaś A. (2001), Metody statystyczne, Polskie Wydawnictwo Ekonomiczne, Warszawa
- Ziuziański P. (2015), Kokpit menedżerski jako narzędzie do wizualizacji danych w kontekście zarządzania wiedzą w organizacji, Ekonomia i Zarządzanie, Oficyna Wydawnictwa Politechniki Białostockiej, nr 1
Autor: Łukasz Nowak, Michał Jurczak