Punktowy diagram korelacji
| Punktowy diagram korelacji |
|---|
| Polecane artykuły |
Punktowy diagram korelacji to jedno z narzędzi, które stosowane są w procesie doskonalenia jakości. Jest to graficzna ilustracja związku zachodzącego między dwoma zmiennymi (cechami). Diagram taki stosujemy, gdy chcemy zbadać zależność pomiędzy dwoma czynnikami, np. zbadać ich zależność przyczynowo- skutkową.
Diagram korelacji służy do:
- "stwierdzenia istnienia zależności pomiędzy zmiennymi,
- stwierdzenia kierunku związku,
- pokazania siły związku."[1]
Tworzenie diagramu korelacji
Diagram korelacyjny otrzymujemy przez naniesienie w prostokątnym kładzie współrzędnych n punktów empirycznych odpowiadających obserwacjom dwóch zmiennych X i Y. Każdą z obserwacji opisujemy parą liczb: xi i yi odpowiadającą punktowi Pi (i = 1,2,..., n) w dwuwymiarowym układzie współrzędnych, gdzie na osi odciętych umieszczamy wartości zmiennej objaśniającej X, a na osi rzędnych - wartości zmiennej objaśnianej Y. W ten sposób otrzymujemy n punktów o współrzędnych (xi, yi). To, w jaki sposób grupowane są punkty na wykresie pokazuje zależności korelacyjne między badanymi zmiennymi. Najprostszy przypadek to liniowa korelacja między zmiennymi.
Typy Korelacji
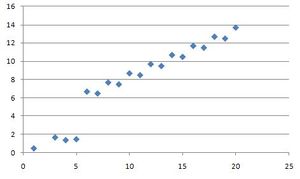
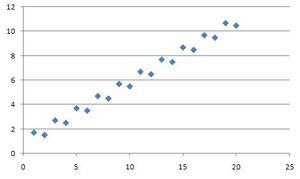
Korelacja dodatnia
Korelacja dodatnia - to przypadek, w którym wzrostowi (spadkowi) wartości jednej zmiennej towarzyszy wzrost (spadek) wartości drugiej zmiennej. Przykładem korelacji dodatniej może być związek między planowaną liczbą dni hospitalizacji pacjenta a szacunkowymi kosztami całkowitymi.
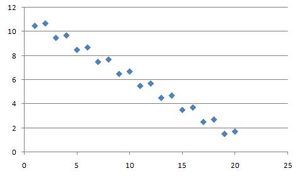
Korelacja ujemna
Korelacja ujemna - to przypadek, w którym wzrostowi (spadkowi) wartości jednej zmiennej towarzyszy spadek (wzrost) wartości drugiej zmiennej.
Brak korelacji
Brak korelacji - nie istnieje widoczna zależność pomiędzy wartościami.
Współczynnik korelacji Pearsona
Relację między dwoma zmiennymi (cechami) można również scharakteryzować przy pomocy współczynnika korelacji Pearsona (rxy), który służy do badania zależności liniowych. Jest on miarą siły związku liniowego pomiędzy zmiennymi mierzalnymi. Bezwzględna wartość współczynnika korelacji informuje o sile związku dwóch cech, natomiast jego znak - o kierunku zależności zachodzącej między dwoma zmiennymi. [2] Tabela poniżej przedstawia zakres współzależności zmiennych w zależności od wartości bezwzględnej rxy.
| Wartość bezwzględna z rxy | Zakres współzależności |
|---|---|
| rxy=0 | Współzależność nie występuje |
| 0< rxy<0,3 | Słaby stopień współzależności |
| 0,3≤ rxy<0,5 | Średni stopień współzależności |
| 0,5≤ rxy<0,7 | Znaczny stopień współzależności |
| 0,7≤ rxy<0,9 | Wysoki stopień współzależności |
| 0,9≤ rxy<1 | Bardzo wysoki stopień współzależności |
| rxy=1 | Współzależność całkowita (ścisłość) |
Źródło: Michalski T., (2008). Statystyka, WSiP, Warszawa, s. 152
Bibliografia
- Bachman P. (2017). Jakość w procesach produkcyjnych, "Problemy inżynierii bezpieczeństwa i nauk o pracy", nr 5, s. 46-47
- Krawczyk M. (red.) (2012). Ekonomia eksperymentalna, Wydawnictwo Wolters Kluwer, Warszawa
- Michalski T., (2008). Statystyka, WSiP, Warszawa
- Opolski K., Dykowska G., Możdżonek M. (2003). Zarządzanie przez jakość w usługach zdrowotnych, Wydawnictwo CeDeWu, Warszawa
- Soliński B., (2006).klasyczne narzędzia zarządzania jakością- Diagram korelacji, Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie, Kraków
- Stabryła A. (red.) (2015). Praktyka projektowania systemów organizacyjnych przedsiębiorstwa, Wydawnictwo Mfiles, Kraków
- Steczkowski J., Zeliaś A. (1997). Metody statystyczne w badaniu zjawisk jakościowych, Akademia Ekonomiczna w Krakowie, Kraków
- Wawak S. (2013). Wybrane koncepcje klasyfikacji metod zarządzania jakością, "Zeszyty Naukowe Uniwersytetu Ekonomicznego w Krakowie", nr 910, s. 37-49
- Żebrowska-Łucyk S. (2015). Praktyczne aspekty zastosowania metod statystycznych w procesach systemu zarządzania, "Pomiary Automatyka Robotyka", nr 2, s. 5-12
Przypisy
- ↑ Soliński B., (2006).klasyczne narzędzia zarządzania jakością- Diagram korelacji, Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie, Kraków
- ↑ Krawczyk M. (red.) (2012). Ekonomia eksperymentalna, Wydawnictwo Wolters Kluwer, Warszawa, s. 82-83
Autor: Danuta Tomera, Sylwia Bierowiec