Notacja AoN: Różnice pomiędzy wersjami
m (cleanup bibliografii i rotten links) |
m (cleanup bibliografii i rotten links) |
||
| Linia 152: | Linia 152: | ||
* Kostrubiec A., (2007), [https://pbc.gda.pl/Content/3907/phd_kostrubiec.pdf ''Analiza skutków ekonomicznych zastosowania wybranych metaheurystyk w harmonogramowaniu projektów''], Politechnika Gdańska, Gdańsk | * Kostrubiec A., (2007), [https://pbc.gda.pl/Content/3907/phd_kostrubiec.pdf ''Analiza skutków ekonomicznych zastosowania wybranych metaheurystyk w harmonogramowaniu projektów''], Politechnika Gdańska, Gdańsk | ||
* PMI (2021), ''A Guide to the Project Management Body of Knowledge (PMBOK® Guide) – Seventh Edition and The Standard for Project Management'' | * PMI (2021), ''A Guide to the Project Management Body of Knowledge (PMBOK® Guide) – Seventh Edition and The Standard for Project Management'' | ||
* Wysocki R. | * Wysocki R. (2013), ''Efektywne zarządzanie projektami. Tradycyjne, zwinne, ekstremalne'', Helion, Gliwice | ||
</noautolinks> | </noautolinks> | ||
Wersja z 18:29, 5 lis 2023
Notacja Activity on the Node (AoN), znana także jako metoda diagramowania pierwszeństwa (ang. precedence diagramming method PDM). Została spopularyzowana wraz z upowszechnieniem komputerów, zastępując Notacja AoA. W tym modelu sieciowym każdy węzeł oznacza zadanie i nazywany jest węzłem działania. Strzałki natomiast reprezentują relacje działania z innymi działaniami - poprzedzającymi to działanie (poprzednikami) i następującymi po nim (następnikami).
Węzeł w diagramie AoN
Węzeł notacji AoN zazwyczaj podzielony jest na siedem pól, gdzie:
- ES (early start) - najwcześniejszy moment rozpoczęcia zadania
- D (duration) - czas trwania zadania
- EF (early finish) - najwcześniejszy moment zakończenia zadania
- LS (late start) - najpóźniejszy moment rozpoczęcia zadania
- F (float) - rezerwa czasowa
- LF (late finish) - najpóźniejszy moment zakończenia zadania
| ES | D | EF |
| Nazwa zadania | ||
| LS | F | LF |
Występuje też wersja, w której węzeł podzielony jest na dziesięć pól, gdzie dodatkowo pojawiają pola:
- Id - identyfikator zadania
- Responsible - osoba odpowiedzialna
- FF (free float) - wolna rezerwa
A pole F (float), tj. rezerwa czasowa, zmienia nazwę na TF (total float) rezerwa całkowita.
| ID | Responsible | D |
| Nazwa zadania | ||
| ES | FF | EF |
| LS | TF | LF |
Obliczanie najwcześniejszego możliwego momentu rozpoczęcia i zakończenia zadania
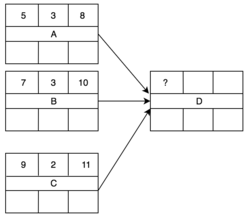
Najwcześniejszy czas rozpoczęcia (ES) zadania, to maksymalny czas spośród możliwych najwcześniejszych czasów zakończenia (EF) poprzedników zadania.
| Zadanie (i) | ES (i) | d (i) | EF (i) = ES (i) + d (i) | Maksimum |
|---|---|---|---|---|
| A | 5 | 3 | 8 | - |
| B | 7 | 3 | 10 | - |
| C | 9 | 2 | 11 | 11 |
Objaśnienie kolumn:
- ES (i) - najwcześniejszy możliwy moment rozpoczęcia zadania "i"
- EF (i) - najwcześniejszy możliwy moment zakończenia zadania "i"
- d (i) - czas trwania zadania “i".
Obliczanie najpóźniejszego możliwego momentu zakończenia i rozpoczęcia zadania
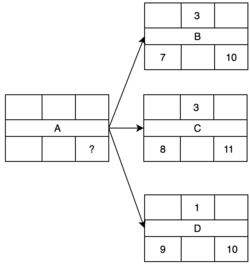
Najpóźniejszy czas zakończenia (LF) zadania, to minimalny czas spośród najpóźniejszego czasu rozpoczęcia (LS) następników zadania.
| Zadanie (i) | LF (i) | d (i) | LS (i) = LF (i) - d (i) | Minimum |
|---|---|---|---|---|
| B | 10 | 3 | 7 | 7 |
| C | 11 | 3 | 8 | - |
| D | 10 | 1 | 9 | - |
Objaśnienie kolumn:
- LF (i) - najpóźniejszy możliwy moment zakończenia zadania "i"
- LS (i) - najpóźniejszy możliwy moment rozpoczęcia zadania "i"
- d (i) - czas trwania zadania “i".
Obliczanie rezerwy całkowitej i ścieżki krytycznej
Rezerwa czasowa w notacji AoN to różnica pomiędzy:
- najpóźniejszym czasem rozpoczęcia zadania (LS), a najwcześniejszym możliwym czasem rozpoczęcia zadania (ES)
- najpóźniejszym czasem zakończenia zadania (LF), a najwcześniejszym możliwym czasem zakończenia zadania (EF)
| ES | D | EF |
| Nazwa zadania | ||
| LS | TF = F = LF - EF = LS - ES | LF |
Ścieżka krytyczna zbudowana jest na węzłach grafu, w którym rezerwa czasowa F jest równa 0.
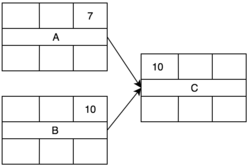
Obliczanie wolnej rezerwy
Wolna rezerwa, to rezerwa czasu zadania, której wykorzystanie nie spowoduje opóźnienia rozpoczęcia następników tego zadania. Występuje ona jedynie dla zadań, w których najwcześniejszy możliwy czas zakończenia (EF) jest mniejszy niż najwcześniejszy czas rozpoczęcia (ES) jego wszystkich następników.
FFi = min (ESj) - EFi, gdzie "j" to wszystkie następniki zadania "i".
Bibliografia
- Grześ A., (2014), Wykres Gantta a metoda ścieżki krytycznej (CPM) , Czasopismo Optimum. Studia Ekonomiczne NR 4 (70) 2014
- Hamilton A., (2001), Managing Projects for Success: A Trilogy, Thomas Telford Publishing Ltd., London, s. 214-223
- Kostrubiec A., (2007), Analiza skutków ekonomicznych zastosowania wybranych metaheurystyk w harmonogramowaniu projektów, Politechnika Gdańska, Gdańsk
- PMI (2021), A Guide to the Project Management Body of Knowledge (PMBOK® Guide) – Seventh Edition and The Standard for Project Management
- Wysocki R. (2013), Efektywne zarządzanie projektami. Tradycyjne, zwinne, ekstremalne, Helion, Gliwice
Autor: Michał Gurgacz