Notacja AoA
| Notacja AoA |
|---|
| Polecane artykuły |
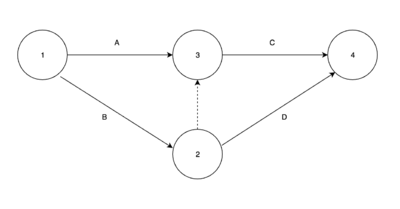
Notacja Activity on the Arrow (AoA), znana także jako Activity Diagramming Method (ADM) czy model strzałkowy. Została po raz pierwszy zastosowana w pierwszej połowie lat 50. ubiegłego wieku w programie rakietowym Polaris. wraz z postęp technik sieciowych oraz rozwojem komputerów wyszła z użycia i jest rzadko wykorzystywana. W tym modelu sieciowym każda strzałka oznacza działanie (gdzie początek strzałki oznacza początek działania, a grot strzałki koniec zadania). Węzły natomiast reprezentują zdarzenia w projekcie i służą do obliczania czasów najwcześniejszego rozpoczęcia zadania i rezerwy czasowej na wykonanie zadania.
Czynność pozorna
W sieci AoA występują tzw. czynności pozorne, czyli takie które odwzorowywują porządek topologiczny pomiędzy rzeczywistymi czynnościami. Czynności pozorne nie zużywają czasu ani zasobów, a zwyczajowo oznaczane są liniami przerywanymi.
| Zadanie | Poprzednik |
|---|---|
| A | - |
| B | - |
| C | A, B |
| D | B, C |
W powyższym przykładzie pomiędzy zdarzeniami 2 i 3 występuje czynność pozorna, która umożliwia rozpoczęcie zadania C dopiero w chwili, gdy zadania A i B zostaną zakończone.
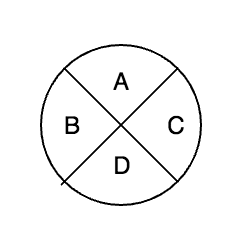
Węzeł w diagramie AoA
Węzeł w notacji AoA zazwyczaj podzielony jest na cztery pola, gdzie w polu:
- A - wpisujemy numer zdarzenia
- B - najwcześniejszy możliwy moment wystąpienia zdarzenia - Tw
- C - najpóźniejszy możliwy moment wystąpienia zdarzenie - Tp
- D - różnice pomiędzy najpóźniejszym momentem a najwcześniejszym momentem wystąpienia zdarzenia (luzem zdarzenia)
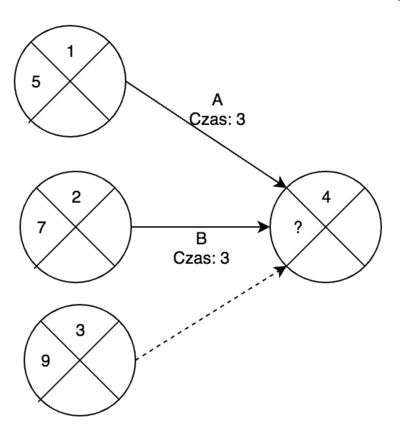
Obliczanie najwcześniejszego możliwego momentu wystąpienia zdarzenia
| Zdarzenie (i) | Tw (i) | Zadanie (z) | t (z) | Tw (i) + t (z) | Maksimum |
|---|---|---|---|---|---|
| 1 | 5 | A | 3 | 8 | - |
| 2 | 7 | B | 3 | 10 | 10 |
| 3 | 9 | - | 0 | 9 | - |
gdzie Tw (i) - najwcześniejszy możliwy moment wystąpienia zdarzenia "i", a t (z) - czas trwania zadania "z".
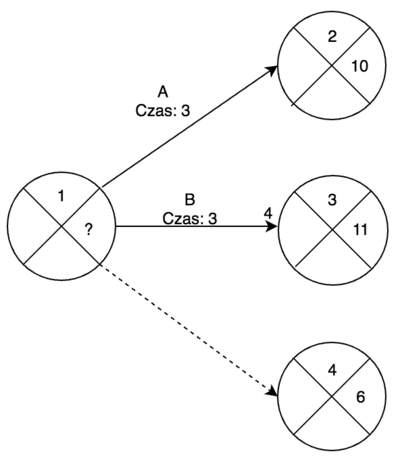
Obliczanie najpóźniejszego możliwego momentu wystąpienia zdarzenia
| Zdarzenie (i) | Tp (i) | Zadanie (z) | t (z) | Tp (i) - t (z) | Minimum |
|---|---|---|---|---|---|
| 2 | 9 | A | 3 | 6 | - |
| 3 | 11 | B | 3 | 8 | - |
| 4 | 7 | - | 0 | 7 | 7 |
gdzie Tp (i) - najpóźniejszy możliwy moment wystąpienia zdarzenia "i", a t (z) - czas trwania zadania "z".
Bibliografia
- Kostrubiec A., (2007), Analiza skutków ekonomicznych zastosowania wybranych metaheurystyk w harmonogramowaniu projektów, Politechnika Gdańska, Gdańsk
- Wysocki R., (2013), Efektywne zarządzanie projektami, Helion, Gliwice, s. 259-261
- Grześ A., (2014), Wykres Gantta a metoda ścieżki krytycznej (CPM) , Czasopismo Optimum. Studia Ekonomiczne NR 4 (70) 2014
- Project Management Institute (2013): Guide to the Project Management Body of Knowledge (PMBOK® Guide) Fifth edition, Management Training & Development Center, Warszawa
- Hamilton A., (2001), Managing Projects for Success: A Trilogy, Thomas Telford Publishing Ltd., London, s. 214-223
Autor: Michał Gurgacz