Prawdopodobieństwo: Różnice pomiędzy wersjami
m (cleanup bibliografii i rotten links) |
m (Dodawanie osieroconych) |
||
| (Nie pokazano 9 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
''' | ''' | ||
Prawdopodobieństwo jest [[Klasyfikacja celów i funkcji|funkcją]], która zdarzeniu ze zbioru zdarzeń elementarnych <math>\Omega\;</math> (zbioru wszystkich możliwych zdarzeń) przypisuje liczbę z przedziału <math>[0,1]\;</math>. Jeżeli jakieś [[zdarzenie]] <math>A\;</math> przyjmuje [[wartość]] równą zero to mówimy, że jest to zdarzenie niemożliwe. | Prawdopodobieństwo jest [[Klasyfikacja celów i funkcji|funkcją]], która zdarzeniu ze zbioru zdarzeń elementarnych <math>\Omega\;</math> (zbioru wszystkich możliwych zdarzeń) przypisuje liczbę z przedziału <math>[0,1]\;</math>. Jeżeli jakieś [[zdarzenie]] <math>A\;</math> przyjmuje [[wartość]] równą zero to mówimy, że jest to zdarzenie niemożliwe. | ||
| Linia 22: | Linia 7: | ||
Prawdopodobieństwo jest funkcją przypisującą liczbę z przedziału [0,1] zdarzeniom ze zbioru zdarzeń elementarnych. Istnieją różne rodzaje prawdopodobieństwa, takie jak klasyczne, warunkowe i całkowite. Drzewo prawdopodobieństwa jest grafem, który obrazuje przebieg zdarzenia losowego. Reguła iloczynów i reguła sum są używane do obliczania prawdopodobieństwa zdarzeń na drzewie. Prawdziwe są również różne własności i działania na zdarzeniach, takie jak suma, iloczyn, różnica i zdarzenia przeciwne. | Prawdopodobieństwo jest funkcją przypisującą liczbę z przedziału [0,1] zdarzeniom ze zbioru zdarzeń elementarnych. Istnieją różne rodzaje prawdopodobieństwa, takie jak klasyczne, warunkowe i całkowite. Drzewo prawdopodobieństwa jest grafem, który obrazuje przebieg zdarzenia losowego. Reguła iloczynów i reguła sum są używane do obliczania prawdopodobieństwa zdarzeń na drzewie. Prawdziwe są również różne własności i działania na zdarzeniach, takie jak suma, iloczyn, różnica i zdarzenia przeciwne. | ||
== Rodzaje == | ==Rodzaje== | ||
''' | ''' | ||
* '''Prawdopodobieństwo klasyczne'''- Jest to prawdopodobieństwo w którym zbiór zdarzeń elementarnych jest skończony oraz składa się on z jednakowo prawdopodobnych zdarzeń elementarnych.Dla zdarzenia <math>A\;</math> ze zbioru zdarzeń elementarnych <math>\Omega\;</math> zachodzi wzór: <math>P (A) = {{|A|}\over{|\Omega|}}</math>, gdzie <math>|A|\;</math> oznacza moc zbioru (ilość jego elementów). | * '''Prawdopodobieństwo klasyczne''' - Jest to prawdopodobieństwo w którym zbiór zdarzeń elementarnych jest skończony oraz składa się on z jednakowo prawdopodobnych zdarzeń elementarnych.Dla zdarzenia <math>A\;</math> ze zbioru zdarzeń elementarnych <math>\Omega\;</math> zachodzi wzór: <math>P (A) = {{|A|}\over{|\Omega|}}</math>, gdzie <math>|A|\;</math> oznacza moc zbioru (ilość jego elementów). | ||
* '''[[Prawdopodobieństwo warunkowe]]''' - Jest to prawdopodobieństwo zajścia zdarzenia <math>A\;</math> pod warunkiem, że zaszło zdarzenie <math>B\;</math> oznaczamy je przez <math>P (A|B)\; </math> i [[dane]] jest ono wzorem: <math>P (A|B) = {{P (A \cap B)}\over{P (B)}}</math>, gdzie <math>P (B)>0\; </math> | |||
* '''[[Prawdopodobieństwo warunkowe]]'''- Jest to prawdopodobieństwo zajścia zdarzenia <math>A\;</math> pod warunkiem, że zaszło zdarzenie <math>B\;</math> oznaczamy je przez <math>P (A|B)\; </math> i [[dane]] jest ono wzorem: <math>P (A|B) = {{P (A \cap B)}\over{P (B)}}</math>, gdzie <math>P (B)>0\; </math> | * '''Prawdopodobieństwo całkowite''' - Jeżeli dla każdego <math>A_i\;</math> ze zbioru zdarzeń elementarnych <math>\Omega\;</math> spełnione są następujące warunki: | ||
* '''Prawdopodobieństwo całkowite'''- Jeżeli dla każdego <math>A_i\;</math> ze zbioru zdarzeń elementarnych <math>\Omega\;</math> spełnione są następujące warunki: | |||
: ''a)'' <math>P (A_i)>0\;</math> dla <math>i=1,..., n\;</math> | : ''a)'' <math>P (A_i)>0\;</math> dla <math>i=1,..., n\;</math> | ||
| Linia 34: | Linia 18: | ||
wtedy dla dowolnego zdarzenia <math>B\;</math> zachodzi wzór: <math>P (B)=\sum_{n = 1}^{n} P (B|A_i)P (A_i)</math> | wtedy dla dowolnego zdarzenia <math>B\;</math> zachodzi wzór: <math>P (B)=\sum_{n = 1}^{n} P (B|A_i)P (A_i)</math> | ||
<google>n</google> | |||
==Drzewo prawdopodobieństwa (stochastyczne)== | |||
Drzewem stochastycznym nazywamy graf, który obrazuje przebieg wielostopniowego zdarzenia losowego. Wierzchołkom takiego drzewa prawdopodobieństwa przyporządkowane są wyniki indywidualnych etapów zdarzenia, krawędziom zaś prawdopodobieństwo ich uzyskania. Suma prawdopodobieństw odpowiadających krawędziom, które wychodzą z tego samego wierzchołka jest równa 1. (Feller W. 2008) | Drzewem stochastycznym nazywamy graf, który obrazuje przebieg wielostopniowego zdarzenia losowego. Wierzchołkom takiego drzewa prawdopodobieństwa przyporządkowane są wyniki indywidualnych etapów zdarzenia, krawędziom zaś prawdopodobieństwo ich uzyskania. Suma prawdopodobieństw odpowiadających krawędziom, które wychodzą z tego samego wierzchołka jest równa 1. (Feller W. 2008) | ||
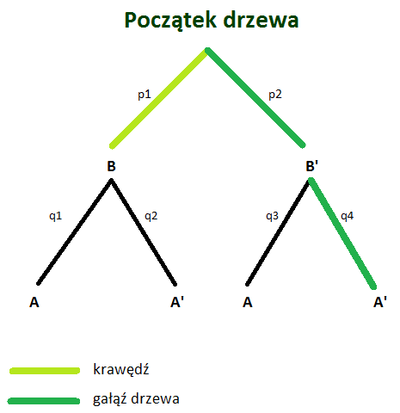
[[Plik:Graf prawdopodobieństwa.png|400px|right|thumb|Rys. 1 przykładowe drzewko doświadczenia dwuetapowego]] | [[Plik:Graf prawdopodobieństwa.png|400px|right|thumb|Rys. 1 przykładowe drzewko doświadczenia dwuetapowego]] | ||
*<math>B\;</math>,<math>B'\;</math> - dwie możliwości wyniku w pierwszej fazie doświadczenia | * <math>B\;</math>,<math>B'\;</math> - dwie możliwości wyniku w pierwszej fazie doświadczenia | ||
* <math>A\;</math>, <math>A'\;</math> - dwie możliwości wyniku w drugiej fazie doświadczenia | * <math>A\;</math>, <math>A'\;</math> - dwie możliwości wyniku w drugiej fazie doświadczenia | ||
*<math>p_1\;</math> - prawdopodobieństwo uzyskania wyniku <math>B\;</math> w pierwszej fazie | * <math>p_1\;</math> - prawdopodobieństwo uzyskania wyniku <math>B\;</math> w pierwszej fazie | ||
*<math>p_2\;</math> - prawdopodobieństwo uzyskania wyniku <math>B'\;</math> w pierwszej fazie | * <math>p_2\;</math> - prawdopodobieństwo uzyskania wyniku <math>B'\;</math> w pierwszej fazie | ||
*<math>q_1\;</math>,<math>q_3\;</math> - prawdopodobieństwo warunkowe uzyskania wyniku <math>A\;</math> w drugiej fazie | * <math>q_1\;</math>,<math>q_3\;</math> - prawdopodobieństwo warunkowe uzyskania wyniku <math>A\;</math> w drugiej fazie | ||
*<math>q_2\;</math>,<math>q_4\;</math> - prawdopodobieństwo warunkowe uzyskania wyniku <math>A'\;</math> w drugiej fazie | * <math>q_2\;</math>,<math>q_4\;</math> - prawdopodobieństwo warunkowe uzyskania wyniku <math>A'\;</math> w drugiej fazie | ||
<math>p_1\;</math> + <math>p_2\;</math> = 0 <math>q_1\;</math> + <math>q_2\;</math> = 0 <math>q_3\;</math> + <math>q_4\;</math> = 0 | <math>p_1\;</math> + <math>p_2\;</math> = 0 <math>q_1\;</math> + <math>q_2\;</math> = 0 <math>q_3\;</math> + <math>q_4\;</math> = 0 | ||
| Linia 52: | Linia 37: | ||
'''Reguła iloczynów'''-prawdopodobieństwo zdarzenia reprezentowanego przez jedną gałąź drzewa jest równe iloczynowi prawdopodobieństw przyporządkowanych krawędziom, z których składa się rozważana gałąź. | '''Reguła iloczynów'''-prawdopodobieństwo zdarzenia reprezentowanego przez jedną gałąź drzewa jest równe iloczynowi prawdopodobieństw przyporządkowanych krawędziom, z których składa się rozważana gałąź. | ||
'''Reguła sum''' - prawdopodobieństwo danego zdarzenia opisanego przez kilka gałęzi jest równe sumie prawdopodobieństw uzyskanych regułą iloczynów dla tych gałęzi | '''Reguła sum''' - prawdopodobieństwo danego zdarzenia opisanego przez kilka gałęzi jest równe sumie prawdopodobieństw uzyskanych regułą iloczynów dla tych gałęzi (Jakubowski J. 2010) | ||
==Podstawowe własności== | |||
Dla dowolnych zdarzeń <math>A\;</math> oraz <math>B\;</math> ze zbioru zdarzeń elementarnych <math>\Omega\;</math> prawdziwe są związki: | Dla dowolnych zdarzeń <math>A\;</math> oraz <math>B\;</math> ze zbioru zdarzeń elementarnych <math>\Omega\;</math> prawdziwe są związki: | ||
: ''a)'' <math>P (A) \geq 0\;</math> | : ''a)'' <math>P (A) \geq 0\;</math> | ||
| Linia 63: | Linia 47: | ||
: ''e)'' <math>P (\Omega) = 1\;</math> | : ''e)'' <math>P (\Omega) = 1\;</math> | ||
== Działania na zdarzeniach== | ==Działania na zdarzeniach== | ||
Działania na zdarzeniach wykonujemy analogicznie do działań na zbiorach. | Działania na zdarzeniach wykonujemy analogicznie do działań na zbiorach. | ||
* Sumą zdarzeń <math>A\;</math> i <math>B\;</math> nazywamy zdarzenie <math>A\;</math> ∪ <math>B\;</math>, któremu sprzyjają zdarzenia elementarne, sprzyjające zdarzeniu <math>A\;</math> lub zdarzeniu <math>B\;</math>. | * Sumą zdarzeń <math>A\;</math> i <math>B\;</math> nazywamy zdarzenie <math>A\;</math> ∪ <math>B\;</math>, któremu sprzyjają zdarzenia elementarne, sprzyjające zdarzeniu <math>A\;</math> lub zdarzeniu <math>B\;</math>. | ||
| Linia 71: | Linia 54: | ||
* Zdarzenie <math>A'\;</math> = <math>\Omega\;</math> \ <math>A\;</math> nazywamy zdarzeniem przeciwnym do zdarzenia <math>A\;</math>. | * Zdarzenie <math>A'\;</math> = <math>\Omega\;</math> \ <math>A\;</math> nazywamy zdarzeniem przeciwnym do zdarzenia <math>A\;</math>. | ||
* Zdarzenia <math>A\;</math> i <math>B\;</math> są zdarzeniami przeciwnymi, jeżeli <math>A\;</math> ∪ <math>B\;</math> = <math>\Omega\;</math> i <math>A\;</math> ∩ <math>B\;</math> = ∅ | * Zdarzenia <math>A\;</math> i <math>B\;</math> są zdarzeniami przeciwnymi, jeżeli <math>A\;</math> ∪ <math>B\;</math> = <math>\Omega\;</math> i <math>A\;</math> ∩ <math>B\;</math> = ∅ | ||
{{infobox5|list1={{i5link|a=[[Zmienna losowa]]}} — {{i5link|a=[[Prawdopodobieństwo warunkowe]]}} — {{i5link|a=[[Pomiar]]}} — {{i5link|a=[[Schemat Bernoulliego]]}} — {{i5link|a=[[Rozkład Poissona]]}} — {{i5link|a=[[Kwartyl]]}} — {{i5link|a=[[Mediana wzór]]}} — {{i5link|a=[[Estymacja]]}} — {{i5link|a=[[Teoria gier]]}} — {{i5link|a=[[Opakowanie wielokrotnego użytku]]}} }} | |||
==Bibliografia== | ==Bibliografia== | ||
<noautolinks> | <noautolinks> | ||
* Feller W. (2008) | * Feller W. (2008), ''Wstęp do rachunku prawdopodobieństwa'', Wydawnictwo Naukowe PWN, Warszawa | ||
* Fisz W. (1969) | * Fisz W. (1969), ''Rachunek prawdopodobieństwa i statystyka matematyczna'', Wydawnictwa Naukowo-Techniczne, Warszawa | ||
* Jakubowski J. (2010) | * Jakubowski J. (2010), ''Wstęp do teorii prawdopodobieństwa'', Wydawnictwo Script, Warszawa | ||
* Krasicki W. (1986) | * Krasicki W. (1986), ''Rachnek prawdopodobieństwa i statystyka matematyczna w zadaniach '', Wydawnictwa Naukowo-Techniczne, Warszawa | ||
* Ombach J. (2000) | * Ombach J. (2000), ''Rachunek prawdopodobieństwa wspomagany komputerowo - MAPLE'', Wydawnictwo Uniwersytetu Jagiellońskiego, Kraków | ||
* Sokołowski | * Sokołowski A. (2004), ''[https://media.statsoft.pl/_old_dnn/downloads/naukowe1.pdf O niewłaściwym stosowaniu metod statystycznych]'', Akademia Ekonomiczna, Kraków | ||
</noautolinks> | </noautolinks> | ||
[[Kategoria: | [[Kategoria:Prawdopodobieństwo]] | ||
{{#metamaster:description|Prawdopodobieństwo to funkcja, która przypisuje zdarzeniom liczbę z przedziału [0,1]. Zdarzenie niemożliwe ma wartość zero, a zdarzenie pewne ma wartość jeden.}} | {{#metamaster:description|Prawdopodobieństwo to funkcja, która przypisuje zdarzeniom liczbę z przedziału [0,1]. Zdarzenie niemożliwe ma wartość zero, a zdarzenie pewne ma wartość jeden.}} | ||
Aktualna wersja na dzień 08:35, 20 lis 2023
Prawdopodobieństwo jest funkcją, która zdarzeniu ze zbioru zdarzeń elementarnych (zbioru wszystkich możliwych zdarzeń) przypisuje liczbę z przedziału . Jeżeli jakieś zdarzenie przyjmuje wartość równą zero to mówimy, że jest to zdarzenie niemożliwe. Jeżeli jakieś zdarzenie przyjmuje wartość równą jeden to mówimy, że jest to zdarzenie pewne.
TL;DR
Prawdopodobieństwo jest funkcją przypisującą liczbę z przedziału [0,1] zdarzeniom ze zbioru zdarzeń elementarnych. Istnieją różne rodzaje prawdopodobieństwa, takie jak klasyczne, warunkowe i całkowite. Drzewo prawdopodobieństwa jest grafem, który obrazuje przebieg zdarzenia losowego. Reguła iloczynów i reguła sum są używane do obliczania prawdopodobieństwa zdarzeń na drzewie. Prawdziwe są również różne własności i działania na zdarzeniach, takie jak suma, iloczyn, różnica i zdarzenia przeciwne.
Rodzaje
- Prawdopodobieństwo klasyczne - Jest to prawdopodobieństwo w którym zbiór zdarzeń elementarnych jest skończony oraz składa się on z jednakowo prawdopodobnych zdarzeń elementarnych.Dla zdarzenia ze zbioru zdarzeń elementarnych zachodzi wzór: , gdzie oznacza moc zbioru (ilość jego elementów).
- Prawdopodobieństwo warunkowe - Jest to prawdopodobieństwo zajścia zdarzenia pod warunkiem, że zaszło zdarzenie oznaczamy je przez i dane jest ono wzorem: , gdzie
- Prawdopodobieństwo całkowite - Jeżeli dla każdego ze zbioru zdarzeń elementarnych spełnione są następujące warunki:
- a) dla
- b) zdarzenia są parami rozłączne
- c)
wtedy dla dowolnego zdarzenia zachodzi wzór:
Drzewo prawdopodobieństwa (stochastyczne)
Drzewem stochastycznym nazywamy graf, który obrazuje przebieg wielostopniowego zdarzenia losowego. Wierzchołkom takiego drzewa prawdopodobieństwa przyporządkowane są wyniki indywidualnych etapów zdarzenia, krawędziom zaś prawdopodobieństwo ich uzyskania. Suma prawdopodobieństw odpowiadających krawędziom, które wychodzą z tego samego wierzchołka jest równa 1. (Feller W. 2008)
- , - dwie możliwości wyniku w pierwszej fazie doświadczenia
- , - dwie możliwości wyniku w drugiej fazie doświadczenia
- - prawdopodobieństwo uzyskania wyniku w pierwszej fazie
- - prawdopodobieństwo uzyskania wyniku w pierwszej fazie
- , - prawdopodobieństwo warunkowe uzyskania wyniku w drugiej fazie
- , - prawdopodobieństwo warunkowe uzyskania wyniku w drugiej fazie
+ = 0 + = 0 + = 0
Gałąź drzewa prawdopodobieństwa - jest to ciąg krawędzi, który prowadzi od początku drzewa do jednego z końcowych jego wierzchołków.
Reguła iloczynów-prawdopodobieństwo zdarzenia reprezentowanego przez jedną gałąź drzewa jest równe iloczynowi prawdopodobieństw przyporządkowanych krawędziom, z których składa się rozważana gałąź.
Reguła sum - prawdopodobieństwo danego zdarzenia opisanego przez kilka gałęzi jest równe sumie prawdopodobieństw uzyskanych regułą iloczynów dla tych gałęzi (Jakubowski J. 2010)
Podstawowe własności
Dla dowolnych zdarzeń oraz ze zbioru zdarzeń elementarnych prawdziwe są związki:
- a)
- b)
- c)
- d)
- e)
Działania na zdarzeniach
Działania na zdarzeniach wykonujemy analogicznie do działań na zbiorach.
- Sumą zdarzeń i nazywamy zdarzenie ∪ , któremu sprzyjają zdarzenia elementarne, sprzyjające zdarzeniu lub zdarzeniu .
- Iloczynem zdarzeń i nazywamy zdarzenie ∩ , któremu sprzyjają zdarzenia elementarne, sprzyjające zdarzeniu i zdarzeniu . Uwaga! Dwa zdarzenia i nazywamy wykluczającymi się (rozłącznymi), jeżeli zdarzenie ∩ jest zdarzeniem niemożliwym, czyli gdy ∩ = ∅.
- Różnicą zdarzeń i nazywamy zdarzenie \ , do którego należą zdarzenia elementarne, sprzyjające zdarzeniu i nie sprzyjające zdarzeniu .
- Zdarzenie = \ nazywamy zdarzeniem przeciwnym do zdarzenia .
- Zdarzenia i są zdarzeniami przeciwnymi, jeżeli ∪ = i ∩ = ∅
| Prawdopodobieństwo — artykuły polecane |
| Zmienna losowa — Prawdopodobieństwo warunkowe — Pomiar — Schemat Bernoulliego — Rozkład Poissona — Kwartyl — Mediana wzór — Estymacja — Teoria gier — Opakowanie wielokrotnego użytku |
Bibliografia
- Feller W. (2008), Wstęp do rachunku prawdopodobieństwa, Wydawnictwo Naukowe PWN, Warszawa
- Fisz W. (1969), Rachunek prawdopodobieństwa i statystyka matematyczna, Wydawnictwa Naukowo-Techniczne, Warszawa
- Jakubowski J. (2010), Wstęp do teorii prawdopodobieństwa, Wydawnictwo Script, Warszawa
- Krasicki W. (1986), Rachnek prawdopodobieństwa i statystyka matematyczna w zadaniach , Wydawnictwa Naukowo-Techniczne, Warszawa
- Ombach J. (2000), Rachunek prawdopodobieństwa wspomagany komputerowo - MAPLE, Wydawnictwo Uniwersytetu Jagiellońskiego, Kraków
- Sokołowski A. (2004), O niewłaściwym stosowaniu metod statystycznych, Akademia Ekonomiczna, Kraków

![{\displaystyle [0,1]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78500cc2eb13225970e52675a8bb405f0fcf6efb)