Metoda Warda: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m (cleanup bibliografii i rotten links) |
||
| (Nie pokazano 54 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
'''Metoda Warda''' Jest tradycyjną i relatywnie najczęściej wykorzystywaną metodą dokonywania analizy skupień. Jest ona efektywna w przypadku gdy liczba jednostek nie jest bardzo liczna (w przypadku metod hierarchicznych rzędu dziesiątek a podziałowych tysięcy jednostek), koncentracje są sferyczne, separowalne, w tych danych nie są wykorzystywane liczne wartości nietypowe i ogólnie określona jest faktyczna liczba skupień (K. Migdal-Najman, K. Najman 2013, s. 180). | '''Metoda Warda''' Jest tradycyjną i relatywnie najczęściej wykorzystywaną metodą dokonywania analizy skupień. Jest ona efektywna w przypadku gdy liczba jednostek nie jest bardzo liczna (w przypadku metod hierarchicznych rzędu dziesiątek a podziałowych tysięcy jednostek), koncentracje są sferyczne, separowalne, w tych danych nie są wykorzystywane liczne wartości nietypowe i ogólnie określona jest faktyczna liczba skupień (K. Migdal-Najman, K. Najman 2013, s. 180). | ||
== Metoda Warda == | ==TL;DR== | ||
Metoda Warda jest popularną metodą analizy skupień, która tworzy strukturę drzewiastą na podstawie minimalizacji wariancji. Jest skuteczna w przypadku małej liczby jednostek i sferycznych, separowalnych koncentracji danych. Metoda ta jest skuteczna w odtwarzaniu realnej struktury danych i tworzeniu skupień o zbliżonych liczebnościach. Wykorzystuje różne miary odległości, takie jak odległość euklidesowa i Czebyszewa. Standaryzowanie zmiennych jest konieczne przed zastosowaniem metody. Metoda Warda jest uważana za jedną z najlepszych metod analizy skupień. | |||
==Metoda Warda== | |||
'''Wykorzystując metodę Warda''' osiągnąć możemy skupienia o zbliżonych liczebnościach, których cechą charakterystyczną jest minimalna wariancja i na tej podstawie również relatywnie często możemy wykorzystywać tę metodę do klasyfikacji jednostek przestrzennych (K. Filipiak 2006, s. 57). | '''Wykorzystując metodę Warda''' osiągnąć możemy skupienia o zbliżonych liczebnościach, których cechą charakterystyczną jest minimalna wariancja i na tej podstawie również relatywnie często możemy wykorzystywać tę metodę do klasyfikacji jednostek przestrzennych (K. Filipiak 2006, s. 57). | ||
'''Metoda Warda''' jest jedną z kilku aglomeracyjnych metod i sposobem grupowania, jak również metodą hierarchiczną, która prowadzi do stworzenia z wielu części analizowanego zbioru struktury drzewiastej (w wersji poziomej nazywana wykresem drzewiastym), natomiast (w pionowej sopelkowym). Na tej podstawie efekty pracy algorytmu ukazywane są w postaci drzewa, które pokazuje następne etapy tworzonej analizy. W taki sposób możemy osiągnąć tzw. ostateczną segmentację składającą się z zorganizowanej kombinacji podziałów na segmenty. | '''Metoda Warda''' jest jedną z kilku aglomeracyjnych metod i sposobem grupowania, jak również metodą hierarchiczną, która prowadzi do stworzenia z wielu części analizowanego zbioru struktury drzewiastej (w wersji poziomej nazywana wykresem drzewiastym), natomiast (w pionowej sopelkowym). Na tej podstawie efekty pracy algorytmu ukazywane są w postaci drzewa, które pokazuje następne etapy tworzonej analizy. W taki sposób możemy osiągnąć tzw. ostateczną segmentację składającą się z zorganizowanej kombinacji podziałów na segmenty. | ||
'''W odniesieniu do''' skuteczności odtworzenia realnej struktury danych zalecane jest wykorzystanie metody Warda. Bazuje ona na regule minimalizacji wariancji. W kontekście metod z tej grupy nie jest konieczne określenie poprzedniego założenia w odniesieniu do wynikowej liczby skupień | '''W odniesieniu do''' skuteczności odtworzenia realnej struktury danych zalecane jest wykorzystanie metody Warda. Bazuje ona na regule minimalizacji wariancji. W kontekście metod z tej grupy nie jest konieczne określenie poprzedniego założenia w odniesieniu do wynikowej liczby skupień - na koniec analizy wykres może być odcięty na adekwatnej wysokości i w tym momencie zinterpretowany (M. Lotko, A. Lotko 2015, s. 6). | ||
# Jest określana jako bardzo skuteczna, natomiast posiadająca inklinację do formułowania skupień o relatywnie małej wielkości. W tej metodzie odległość pomiędzy skupieniami określana jest jako różnica między sumami kwadratów odchyleń konkretnych jednostek od środka ciężkości grup, do których punkty te są przypisywane. Minimum rozróżnienia wartości cech, będących kryterium segmentacji jest kryterium grupowania jednostek w kolejne skupienia, na podstawie wartości średnich skupień formułowanych w następnych etapach (M. Adamowicz, P. Janulewicz 2012, s. 24). | # Jest określana jako bardzo skuteczna, natomiast posiadająca inklinację do formułowania skupień o relatywnie małej wielkości. W tej metodzie odległość pomiędzy skupieniami określana jest jako różnica między sumami kwadratów odchyleń konkretnych jednostek od środka ciężkości grup, do których punkty te są przypisywane. Minimum rozróżnienia wartości cech, będących kryterium segmentacji jest kryterium grupowania jednostek w kolejne skupienia, na podstawie wartości średnich skupień formułowanych w następnych etapach (M. Adamowicz, P. Janulewicz 2012, s. 24). | ||
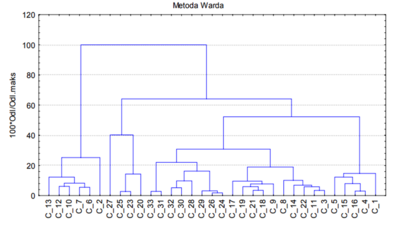
[[Plik:Metoda Warda wykres.png|thumb|400px|Rysunek 1. Aglomeracja metodą Warda (A. Wałęga, S. Krzanowski, K. Chmielowski 2009)]] | |||
# Znacznie różni się od pozostałych, ponieważ odległości pomiędzy skupieniami opisywane są na podstawie analizy wariancji. Jest to metoda polegająca na minimalizacji sumy kwadratów odchyleń wewnątrz skupień. Na każdym poziomie z wszelkich dostępnych i możliwych do łączenia par skupień dokonuje się wyboru tej, która w efekcie łączenia daje skupienie o minimalnym rozróżnieniu Miarą zróżnicowania skupienia w odniesieniu do wartości średnich jest ESS (Error Sum of Squares), które nazywane jest także błędem sumy kwadratów (A. Wałęga, S. Krzanowski, K. Chmielowski 2009, s. 73). | # Znacznie różni się od pozostałych, ponieważ odległości pomiędzy skupieniami opisywane są na podstawie analizy wariancji. Jest to metoda polegająca na minimalizacji sumy kwadratów odchyleń wewnątrz skupień. Na każdym poziomie z wszelkich dostępnych i możliwych do łączenia par skupień dokonuje się wyboru tej, która w efekcie łączenia daje skupienie o minimalnym rozróżnieniu Miarą zróżnicowania skupienia w odniesieniu do wartości średnich jest ESS (Error Sum of Squares), które nazywane jest także błędem sumy kwadratów (A. Wałęga, S. Krzanowski, K. Chmielowski 2009, s. 73). | ||
<google>n</google> | |||
==ESS jest opisane wzorem== | |||
<math>\sum_{i=1}^k (x_{i}-\overline{x})^2</math> | <math>\sum_{i=1}^k (x_{i}-\overline{x})^2</math> | ||
Gdzie | |||
* | * | ||
<math>x_i</math> - Wartość zmiennej będącej kryterium segmentacji dla i-tego obiektu | <math>x_i</math> - Wartość zmiennej będącej kryterium segmentacji dla i-tego obiektu | ||
| Linia 20: | Linia 25: | ||
<math>k</math> - Liczba obiektów w skupieniu | <math>k</math> - Liczba obiektów w skupieniu | ||
==Efektywność metody Warda== | |||
'''Na bazie własności teoretycznych hierarchicznych metod aglomeracyjnych''', jak również efektów badań symulacyjnych Grabiński i Sokołowski określili że najlepszą metodą jest metoda Warda, której efektywność wykrywania faktycznej struktury danych jest mniej więcej 40% większa niż dalsza w kolejności metoda najdalszego sąsiedztwa. Do analogicznych wniosków doszedł też Milligan. Metoda Warda jest dostępna w popularnie dziś wykorzystywanych komputerowych pakietach statystycznych. Statistica, przy wykorzystaniu której dokonywano analizy na potrzeby niniejszego opracowania, pozwala na dokonanie wyboru - jako kryterium podobieństwa obiektów w odniesieniu do siedmiu miar odległości, tj. kwadrat odległości euklidesowej, odległość euklidesowa, odległość miejska, odległość Czebyszewa, odległość potęgowa, niezgodność procentowa oraz 1-r Pearsona. Przegląd wielu pozycji literatury i znajomość znajdujących się w niej opinii ekspertów umożliwia zauważyć, że w odniesieniu do metody Warda, z siedmiu miar odległości, w badaniach empirycznych najczęściej wykorzystywane są dwie pierwsze. W zwyczajowym ujęciu, opisanym przez Warda, zwracana jest uwaga na wymóg kwadratu odległości euklidesowej do oceny podobieństwa obiektów. Warto zauważyć, że pomimo iż inne miary odległości nie mają interpretacji geometrycznej to w ujęciu praktycznym relatywnie często alternatywnie używana jest odległość euklidesowa (R. Klóska 2017, s. 147). | |||
* Oblicza się ja następującymi wzorami: | |||
== | ==Odległość Czebyszewa== | ||
<math> d(x,y) = max \begin{vmatrix}x_i - y_i\end{vmatrix}</math> | <math> d(x,y) = max \begin{vmatrix}x_i - y_i\end{vmatrix}</math> | ||
<math> d(x,y) = \sqrt\sum_{i=1}^p \begin{vmatrix}x_i - y_i\end{vmatrix}^2</math> | ==Odległość Euklidesowa== | ||
<math> d(x,y) = \sqrt{\sum_{i=1}^p \begin{vmatrix}x_i - y_i\end{vmatrix}^2}</math> | |||
* Jest to najczęściej wybierana metryka, jako najbardziej "naturalna" | |||
==Odległość miejska (Manhattan)== | |||
<math> d(x,y) = \sum_{i=1}^p \begin{vmatrix}x_i - y_i\end{vmatrix}</math> | |||
* W tej metryce sfera jest powierzchnią kostki | |||
==Odległość euklidesowa do kwadratu== | |||
<math> d(x,y) = \sum_{i=1}^p \begin{vmatrix}x_i - y_i\end{vmatrix}^2</math> | |||
'''Aby było możliwe''' korzystać z wyżej opisanych metryk, różne zmienne muszą być porównywalne. | |||
Z tego powodu powinno się dokonać wstępnego standaryzowania zmiennych. W praktyce bardzo często standaryzuje się | |||
zmienne na podstawie wzoru: <math>z_i = \dfrac{x_i - \overline{x}}{S_x}</math> gdzie <math>x_i</math> to średnia, zaś <math>s_x</math> to odchylenie standardowe zmiennej w próbie. Dokonanie wyboru właściwej metryki pozwala na wykreowanie kwadratowej macierzy odległości. Macierz taka jest symetryczna <math>(d_{ij} = d_{ji})</math> oraz na głównej przekątnej ma zera <math>(d_{ii} = 0)</math> (D. Pawlak 2014/2015). | |||
{{infobox5|list1={{i5link|a=[[Metoda punktacji]]}} — {{i5link|a=[[Skala Likerta]]}} — {{i5link|a=[[Mediana wzór]]}} — {{i5link|a=[[Skala pomiaru]]}} — {{i5link|a=[[Kwartyl]]}} — {{i5link|a=[[Wartościowanie jakości]]}} — {{i5link|a=[[Metody taksonomiczne]]}} — {{i5link|a=[[Współczynnik zmienności]]}} — {{i5link|a=[[Analiza przyczynowa]]}} }} | |||
==Bibliografia== | ==Bibliografia== | ||
* Adamowicz M. Janulewicz P. (2012) | <noautolinks> | ||
* Filipiak K. (2006) | * Adamowicz M., Janulewicz P. (2012), ''Wykorzystanie metod wielowymiarowych w określeniu pozycji konkurencyjnej gminy na przykładzie województwa lubelskiego'', Metody Ilościowe w Badaniach Ekonomicznych, nr 1 | ||
* Klóska R. (2017) | * Filipiak K. (2006), ''Metody statystyczne stosowane do oceny regionalnego zróżnicowania rolnictwa'', Raporty PiB, nr 3 | ||
* Lotko M. Lotko A. (2015) | * Klóska R. (2017), ''Proinnowacyjny rozwój regionalny w Polsce jako kryterium analizy skupień'', Ekonomiczne Problemy Usług, nr 4 | ||
* Migdal-Najman K. Najman K. (2013) | * Lotko M., Lotko A. (2015), ''Zastosowanie analizy skupień do oceny zagrożeń zawodowych pracowników wiedzy i ich postaw wobec charakteru pracy'', Eksploatacja i Niezawodność, nr 17 | ||
* Wałęga A. Krzanowski S. Chmielowski K. (2009) | * Migdal-Najman K., Najman K. (2013), ''Analiza porównawcza wybranych metod analizy skupień w grupowaniu jednostek o złożonej strukturze grupowej'', Zarządzanie i Finanse, nr 3 | ||
* Pawlak D. (2015), ''[https://home.agh.edu.pl/~mmd/_media/dydaktyka/adp/analiza_skupien.pdf Laboratorium IX: Analiza skupień]'', Statistica | |||
* Wałęga A. Krzanowski S. Chmielowski K. (2009), ''[https://agro.icm.edu.pl/agro/element/bwmeta1.element.agro-48d90932-872b-4fd0-a74c-c4315bd5f221/c/Walega.pdf Wykorzystanie metody analizy skupień do identyfikacji jednorodnych zlewni pod względem indeksów powodziowości i wybranych charakterystyk fizjograficznych]'', Infrastruktura i Ekologia Terenów Wiejskich, nr 6 | |||
</noautolinks> | |||
[[Kategoria:Ekonometria]]. | |||
{{a|Magdalena Mikołajek}}. | |||
{{#metamaster:description|Metoda Warda - tradycyjna i często stosowana analiza skupień, idealna dla niewielkiej liczby jednostek i sferycznych koncentracji. Pozwala określić liczbę skupień.}} | |||
Aktualna wersja na dzień 12:50, 6 sty 2024
Metoda Warda Jest tradycyjną i relatywnie najczęściej wykorzystywaną metodą dokonywania analizy skupień. Jest ona efektywna w przypadku gdy liczba jednostek nie jest bardzo liczna (w przypadku metod hierarchicznych rzędu dziesiątek a podziałowych tysięcy jednostek), koncentracje są sferyczne, separowalne, w tych danych nie są wykorzystywane liczne wartości nietypowe i ogólnie określona jest faktyczna liczba skupień (K. Migdal-Najman, K. Najman 2013, s. 180).
TL;DR
Metoda Warda jest popularną metodą analizy skupień, która tworzy strukturę drzewiastą na podstawie minimalizacji wariancji. Jest skuteczna w przypadku małej liczby jednostek i sferycznych, separowalnych koncentracji danych. Metoda ta jest skuteczna w odtwarzaniu realnej struktury danych i tworzeniu skupień o zbliżonych liczebnościach. Wykorzystuje różne miary odległości, takie jak odległość euklidesowa i Czebyszewa. Standaryzowanie zmiennych jest konieczne przed zastosowaniem metody. Metoda Warda jest uważana za jedną z najlepszych metod analizy skupień.
Metoda Warda
Wykorzystując metodę Warda osiągnąć możemy skupienia o zbliżonych liczebnościach, których cechą charakterystyczną jest minimalna wariancja i na tej podstawie również relatywnie często możemy wykorzystywać tę metodę do klasyfikacji jednostek przestrzennych (K. Filipiak 2006, s. 57).
Metoda Warda jest jedną z kilku aglomeracyjnych metod i sposobem grupowania, jak również metodą hierarchiczną, która prowadzi do stworzenia z wielu części analizowanego zbioru struktury drzewiastej (w wersji poziomej nazywana wykresem drzewiastym), natomiast (w pionowej sopelkowym). Na tej podstawie efekty pracy algorytmu ukazywane są w postaci drzewa, które pokazuje następne etapy tworzonej analizy. W taki sposób możemy osiągnąć tzw. ostateczną segmentację składającą się z zorganizowanej kombinacji podziałów na segmenty.
W odniesieniu do skuteczności odtworzenia realnej struktury danych zalecane jest wykorzystanie metody Warda. Bazuje ona na regule minimalizacji wariancji. W kontekście metod z tej grupy nie jest konieczne określenie poprzedniego założenia w odniesieniu do wynikowej liczby skupień - na koniec analizy wykres może być odcięty na adekwatnej wysokości i w tym momencie zinterpretowany (M. Lotko, A. Lotko 2015, s. 6).
- Jest określana jako bardzo skuteczna, natomiast posiadająca inklinację do formułowania skupień o relatywnie małej wielkości. W tej metodzie odległość pomiędzy skupieniami określana jest jako różnica między sumami kwadratów odchyleń konkretnych jednostek od środka ciężkości grup, do których punkty te są przypisywane. Minimum rozróżnienia wartości cech, będących kryterium segmentacji jest kryterium grupowania jednostek w kolejne skupienia, na podstawie wartości średnich skupień formułowanych w następnych etapach (M. Adamowicz, P. Janulewicz 2012, s. 24).
- Znacznie różni się od pozostałych, ponieważ odległości pomiędzy skupieniami opisywane są na podstawie analizy wariancji. Jest to metoda polegająca na minimalizacji sumy kwadratów odchyleń wewnątrz skupień. Na każdym poziomie z wszelkich dostępnych i możliwych do łączenia par skupień dokonuje się wyboru tej, która w efekcie łączenia daje skupienie o minimalnym rozróżnieniu Miarą zróżnicowania skupienia w odniesieniu do wartości średnich jest ESS (Error Sum of Squares), które nazywane jest także błędem sumy kwadratów (A. Wałęga, S. Krzanowski, K. Chmielowski 2009, s. 73).
ESS jest opisane wzorem
Gdzie
- Wartość zmiennej będącej kryterium segmentacji dla i-tego obiektu
- Liczba obiektów w skupieniu
Efektywność metody Warda
Na bazie własności teoretycznych hierarchicznych metod aglomeracyjnych, jak również efektów badań symulacyjnych Grabiński i Sokołowski określili że najlepszą metodą jest metoda Warda, której efektywność wykrywania faktycznej struktury danych jest mniej więcej 40% większa niż dalsza w kolejności metoda najdalszego sąsiedztwa. Do analogicznych wniosków doszedł też Milligan. Metoda Warda jest dostępna w popularnie dziś wykorzystywanych komputerowych pakietach statystycznych. Statistica, przy wykorzystaniu której dokonywano analizy na potrzeby niniejszego opracowania, pozwala na dokonanie wyboru - jako kryterium podobieństwa obiektów w odniesieniu do siedmiu miar odległości, tj. kwadrat odległości euklidesowej, odległość euklidesowa, odległość miejska, odległość Czebyszewa, odległość potęgowa, niezgodność procentowa oraz 1-r Pearsona. Przegląd wielu pozycji literatury i znajomość znajdujących się w niej opinii ekspertów umożliwia zauważyć, że w odniesieniu do metody Warda, z siedmiu miar odległości, w badaniach empirycznych najczęściej wykorzystywane są dwie pierwsze. W zwyczajowym ujęciu, opisanym przez Warda, zwracana jest uwaga na wymóg kwadratu odległości euklidesowej do oceny podobieństwa obiektów. Warto zauważyć, że pomimo iż inne miary odległości nie mają interpretacji geometrycznej to w ujęciu praktycznym relatywnie często alternatywnie używana jest odległość euklidesowa (R. Klóska 2017, s. 147).
- Oblicza się ja następującymi wzorami:
Odległość Czebyszewa
Odległość Euklidesowa
- Jest to najczęściej wybierana metryka, jako najbardziej "naturalna"
Odległość miejska (Manhattan)
- W tej metryce sfera jest powierzchnią kostki
Odległość euklidesowa do kwadratu
Aby było możliwe korzystać z wyżej opisanych metryk, różne zmienne muszą być porównywalne. Z tego powodu powinno się dokonać wstępnego standaryzowania zmiennych. W praktyce bardzo często standaryzuje się zmienne na podstawie wzoru: gdzie to średnia, zaś to odchylenie standardowe zmiennej w próbie. Dokonanie wyboru właściwej metryki pozwala na wykreowanie kwadratowej macierzy odległości. Macierz taka jest symetryczna oraz na głównej przekątnej ma zera (D. Pawlak 2014/2015).
| Metoda Warda — artykuły polecane |
| Metoda punktacji — Skala Likerta — Mediana wzór — Skala pomiaru — Kwartyl — Wartościowanie jakości — Metody taksonomiczne — Współczynnik zmienności — Analiza przyczynowa |
Bibliografia
- Adamowicz M., Janulewicz P. (2012), Wykorzystanie metod wielowymiarowych w określeniu pozycji konkurencyjnej gminy na przykładzie województwa lubelskiego, Metody Ilościowe w Badaniach Ekonomicznych, nr 1
- Filipiak K. (2006), Metody statystyczne stosowane do oceny regionalnego zróżnicowania rolnictwa, Raporty PiB, nr 3
- Klóska R. (2017), Proinnowacyjny rozwój regionalny w Polsce jako kryterium analizy skupień, Ekonomiczne Problemy Usług, nr 4
- Lotko M., Lotko A. (2015), Zastosowanie analizy skupień do oceny zagrożeń zawodowych pracowników wiedzy i ich postaw wobec charakteru pracy, Eksploatacja i Niezawodność, nr 17
- Migdal-Najman K., Najman K. (2013), Analiza porównawcza wybranych metod analizy skupień w grupowaniu jednostek o złożonej strukturze grupowej, Zarządzanie i Finanse, nr 3
- Pawlak D. (2015), Laboratorium IX: Analiza skupień, Statistica
- Wałęga A. Krzanowski S. Chmielowski K. (2009), Wykorzystanie metody analizy skupień do identyfikacji jednorodnych zlewni pod względem indeksów powodziowości i wybranych charakterystyk fizjograficznych, Infrastruktura i Ekologia Terenów Wiejskich, nr 6
.
Autor: Magdalena Mikołajek
.